基于时频分析与相关系数算法的目标探测与距离估计方法研究
杜晨阳,沈俊逸,刘扬扬,李 晨,陈 晨
(上海机电工程研究所,上海 201109)
0 引 言
现代战争的全方位、多层次、大纵深特性使得目标隐蔽性越来越高,目标的背景环境越来越复杂[1],由此引发出对强杂波背景环境下雷达探测能力的要求也越来越高。此类雷达探测技术在民用方面也有很高的利用价值,比如在人工智能大趋势下发展的自动驾驶技术、防撞技术、自动避让技术[2-4]等就对车载雷达的探测能力有很高的需求。
有效的目标探测应能对抗天气和光线的影响,达到全天候使用的效果,同时也要求具备动态实时测试的能力[5]。在此需求下,军民双方都在大力发展基于微波/毫米波雷达的低慢小目标探测技术[6]。
本文将探讨一种基于时频分析和相关系数的雷达信号处理算法,解决强杂波背景环境下区分低慢小目标与背景环境的问题,再进一步运用距离外推算法推算弱加速度目标在未来短时间内的距离位置信息。
1 信号模型
假设线性调频连续波(linear frequency-modulated continuous wave,LFMCW)雷达发射信号[7]为锯齿波信号,则其在调频周期内的信号表达式为
(1)
式中:A是发射信号的幅度;f0是载波频率;k调频斜率,k=±B/T(B是调频带宽,T是调频周期);t表示时间。信号如图1所示。

图1 线性调频连续波雷达信号Fig.1 Linear frequency-modulated continuous wave radar signal
某一目标与雷达初始距离为R0,径向速度v,回波信号则可表示为
(2)
式中:A0为回波信号幅度;τ为信号时延。
(3)
式中:R为目标与雷达间的距离;c为光速。
中频信号来自于接收信号与发射信号的下混频,经差频解调法获得的差频信号表达式为
(4)
式中:sk为差频信号。
将式(3)代入式(4),可将中频信号表示为
(5)
(6)
(7)
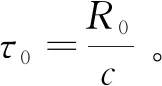
式(5)所得的中频信号仍为线性调频信号,其参数表示为
(8)
(9)

(10)
式中:Bm为带宽;fm为由回波时延与目标运动引入的多普勒频率;φm为时延引入的相位。
经过AD采样,得到离散信号表达式为
sk(t,n)=AA0exp(jφm)×
(11)
式中:n为采样点的序号;Ts为采样周期。
对AD采样后的结果作傅里叶变换,可以获得复包络的表达式为
(12)
(13)
可以观察到复包络中包含有目标的距离信息和速度信息,对应关系分别表示为
(14)
(15)
式中:fi为发射信号与每一路接收信号下变频所得信号频率;fv为接收信号包含的多普勒频率。借助二维傅里叶变换,就可以提取出距离与速度信息。其距离维和速度维的分辨率表示为
(16)
(17)
式中:fs是AD采样率;N是一维傅里叶变换点数;M是二维傅里叶变换点数。
本文在二维傅里叶变换分析信号基础上,运用矩形窗对信号作短时傅里叶变换[8-9],如图2所示。
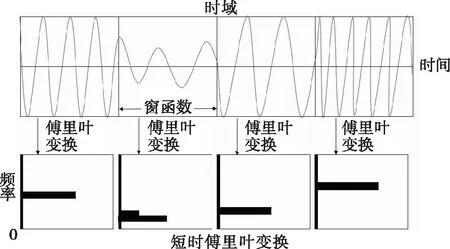
图2 短时傅里叶变换Fig.2 Short-time Fourier transform
相较于傅里叶变换,短时傅里叶变换可以准确地将信号的频率分量作为时间的函数来进行监控。用一个窗函数将信号分为若干段,对每一段都分别作傅里叶变换,就可以得到一个随时间变化的频谱,其表达式为
STFTs,γ(t,f)=
(18)
式中:γ(t)为所采用的窗函数。这也是短时傅里叶变换和传统傅里叶变换最为关键的区别。因为分析的信号在时间域不再是无限长,就可以将信号的频域图谱作为时间的因变量,监控其变化情况。
2 算法设计
探测复杂环境背景下的静止目标尤其是人体目标时,受限于目标的雷达散射截面积[10](radar cross section, RCS)大小,会出现目标被背景淹没、目标被剔除的情况,容易对距离维检测造成影响。为了解决强杂波环境背景下对静止目标的探测问题,本文借鉴红外弱小目标检测算法中“滤除属于背景的部分区域”的思想[11],在二维FFT检测之后引入相关系数[12]算法,对强杂波背景环境下的静止目标进行筛选。

定义当前时刻探测到的距离维信息与强杂波背景环境信息的协方差为

(19)
定义其相关系数为
(20)
式中:D1(S)、D2(T)表示S和T方差。
根据协方差的定义可知,协方差所表征的是S的偏差与T的偏差的乘积的数学期望。协方差可正可负,所以根据式(20)可知,相关系数也可正可负。一般用相关系数的绝对值来判断目标的相对关系。计算所得的相关系数绝对值越小,表明目标区域的实时情况数据和背景环境数据之间的相关性越弱,因此可以通过计算相关系数来进行目标探测。通常认为相关系数的绝对值在0~0.1时为不相关,0.1~0.3为弱相关,0.3~0.5为中等相关,0.5~1.0为强相关。以此作为依据,以0.3和0.7为界,设定相关性判定阈值,即相关系数小于0.3时,判定为弱相关,即存在背景环境之外的目标;相关系数大于0.7时,判定为强相关,认为没有目标进入。
在算法实现过程中,每40 ms对窗函数截取的信号做二维FFT和相关系数计算。在二维FFT的结果中取其峰值为目标,结合时移的窗函数就可以得到目标的速度信息随时间的变化情况。取二维FFT的距离维信息做相关系数计算,取相关系数的谷值为目标。对野值采用“线性取值”的方法进行剔除。
假设目标当前与雷达距离为R1,目标当前时刻与雷达之间的连线速度为v1,目标加速度为aa,时刻目标与雷达距离为R2,时刻目标与雷达之间的连线速度为v2,则有
v2=v1+aaτ′
(21)
(22)
根据式(21)和式(22)可以在一定条件下设计距离外推算法。若目标不具有明显的加速度,结合时频分析所得的速度信息与相关系数算法给出的目标当前距离信息,利用距离外推算法,估计获得目标在下一帧的距离信息。
3 实验环境及结果分析
本文在铁道路口采集3组没有人体目标时的背景环境数据,经过算法计算,可得环境间相关系数如图3所示,处理结果见表1。

表1 环境间相关系数处理结果Tab.1 The result of the correlation coefficients of environment

图3 环境间相关系数Fig.3 The correlation coefficients of environment
正如预期,计算所得的相关系数超过了0.7,各组环境数据之间的相关性比较强,验证了相关系数判别阈值的可行性。
采集人体目标骑行时的数据,处理结果如图4所示,每40 ms输出一帧数据,通过时频分析得到了人体目标骑行速度随时间的变化情况。
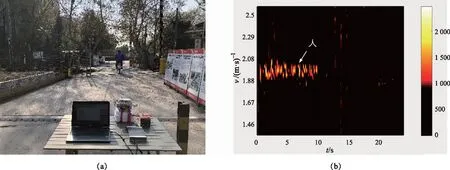
图4 人体目标骑行时的数据Fig.4 The Data of Riding target
人体目标保持静止时,采集其在不同位置时的数据,通过二维FFT+时频分析算法得到的结果均如图5所示,人体目标回波与背景环境的回波混杂在一起,无法准确识别出人体目标。在信号处理算法的设计中,此时会继续计算实时数据与背景环境数据间的相关系数,获得的结果如图6所示。

图5 静止目标二维FFT结果Fig.5 2-D FFT result of motionless target

图6 静止目标相关系数Fig.6 The correlation coefficients of motionless target
将图6的处理结果数据列于表2中。

表2 静止目标相关系数处理结果Tab.2 The result of the correlation coefficients of motionless target
从处理结果可以看出,计算所得的相关系数都小于0.3,由于人体目标的存在,使得实时数据与背景环境数据有明显的弱相关性。再通过提取相关系数的最小值,获得了人体目标的距离信息。
此算法同样可以得到运动目标的距离变化情况,如图7所示。采集、分析了人体目标近乎匀速从远处走近时的数据,通过计算相关系数反映出了正确的人体目标距离变化信息。

图7 行人目标相关系数Fig.7 The correlation coefficients of walking target
对于运动目标,根据二维FFT所得的速度信息与相关系数计算所得的当前距离信息,可以外推出下一时刻目标所处的距离维位置,如图8所示。由于人体目标行走速度比较缓慢,以280 ms为周期提取数据。选取的第1帧和第2帧数据如图8(a)和图8(b)所示,通过距离外推算法获得第3帧数据,然后继续外推所得的第4帧和第5帧数据如图8(c)和图8(d)所示,实测所得的第4帧和第5帧数据如图8(e)和图8(f)所示。x轴为距离维,y轴为速度维,z轴为幅度。距离外推算法结果数据见表3。

图8 距离外推算法结果Fig.8 The result of range extrapolation

表3 距离外推算法结果Tab.3 The result of range extrapolation
根据图8与表3可知,匀速运动外推的距离信息与实测的结果基本吻合,验证了距离外推算法的可行性。
4 结束语
本文针对强杂波背景环境下难以区分低慢小目标与背景环境的问题,设计了一种基于时频分析和相关系数计算的雷达信号处理算法,并用一个工作在X波段的线性调频连续波雷达采集数据,对算法进行验证。实验结果表明,本文所设计的算法可以从强杂波背景环境回波中获取低慢小目标的速度信息与距离信息,并且可以推算出弱加速度运动目标在未来短时间内的距离信息。然而该算法对于加速度较大的目标仍不具备运动行为推算能力,在后续的研究中应开展加速度补偿工作,从而应用到更广泛的场景中。

