基于固定时间收敛的终端角约束滑模制导律设计

张晓宇，张 鹏，郑 鑫，倪元华

(1. 南开大学人工智能学院,天津 300350； 2. 哈尔滨工程大学智能科学与工程学院,黑龙江 哈尔滨 150001； 3. 上海航天技术研究院，上海 201109)

0 引 言

随着技术的发展，现代战争对导弹拦截目标的要求也不断提高，不仅希望导弹拦截目标的脱靶量最小，而且要求导弹以指定的角度拦截目标以实现对目标最大的摧毁效果。为了满足特殊制导任务的需求，需要对带有终端角约束的制导律进行进一步研究[1]。比例导引法由于其结构简单、便于应用的特点被广泛应用于带有终端角约束的制导方法中[2-3]。然而，比例导引法对于大机动目标的拦截，不能达到所要求的拦截精度。

变结构控制由于其能有效抑制系统不确定性而被广泛应用于制导律设计中[4-5]。由于导弹拦截目标的末制导阶段时间短，因此提出了一些基于变结构滑模控制的有限时间收敛制导律[6-8]。但是这些制导律的收敛时间依赖导弹制导系统的初始状态，如果制导系统的初始状态选择不当会导致制导系统状态收敛时间无穷大。

针对上述问题，本文提出一种基于固定时间收敛的终端角度约束滑模制导律[9]，针对目标机动，设计一种固定时间收敛的扰动观测器，可实现系统扰动的固定时间估计，并在此基础上证明了制导系统的固定时间稳定特性。

1 数学建模

假设导弹与目标均为质点，则导弹与目标的平面作战运动关系如图1所示。M和T代表导弹和目标，vM与vT代表导弹与目标的速度，aM与aT代表导弹与目标的加速度，θM与θT代表导弹与目标的航迹角，r与q分别代表弹-目的相对距离和视线角。

图1 导弹与目标的平面作战相对关系Fig.1 The planar engagement between missile and target

不失一般性，设计制导律时引入如下假设：

1) 假设1：在末制导阶段，导弹与目标的速度大小不变。

2) 假设2：导弹与目标的导引头和执行机构动态特性是理想的，即不考虑控制指令延迟。

则导弹与目标在极坐标系下的相对运动方程如式(1)所示[10]。

(1)

(2)

(3)

本文的目的是设计制导律aM，在保证导弹有较小的脱靶量的同时，状态变量x1和x2在有界的有限时间内收敛到足够小且接近于零的邻域。技术上讲，当r∈[rmin,rmax]时，导弹可以实现对目标的碰撞拦截，其中rmin和rmax代表较小的正常数。

2 定义及引理

定义1： 考虑式(4)所示非线性系统

(4)

式中：x∈Rn是状态，f(x(t)):D→Rn是非线性函数。如果式(4)表示的系统是有限时间稳定的并且收敛时间T(x0)∈R一致有界，若存在正常数Tmax满足T(x0)≤Tmax,∀x0∈Rn，那么式(4)表示的系统是固定时间稳定的[13]。

引理1[9]： 设计如式(5)所示的系统，即

(5)

(6)

(7)

对式(7)所描述的非线性导弹-目标动力学构造一个三阶固定时间扰动观测器

(8)

(9)

3 固定时间收敛的终端角约束制导律设计与分析

非奇异固定时间收敛滑模面设计如式(10)所示。

(10)

φ(x1)=

(11)

(12)

式中：p1和q1是两个正奇数满足q1>p1；l1=(2-p1/q1)εp1/q1-1,l2=(p1/q1-1)εp1/q1-2，并且ε是一个充分小的正常数。

定理1： 针对式(3)所示系统，设计式(10)固定时间收敛滑模面，考虑式(8)设计的固定时间扰动观测器，设计制导律为

(13)

φ(x1)=

(14)

由此可得：

1) 滑模变量固定时间内收敛于

(15)

2)状态变量固定时间内收敛于

(16)

固定时间T将在证明中给出。

证明：考虑如下李雅普诺夫函数

V=s2

(17)

对式(17)进行微分并代入式(3)，可得

(18)

将式(13)制导律代入到式(18)，可得

(19)

式中，a1≤N(s)<1。

式(19)可进一步转化为式(20)和(21)两种形式，即

(20)

(21)

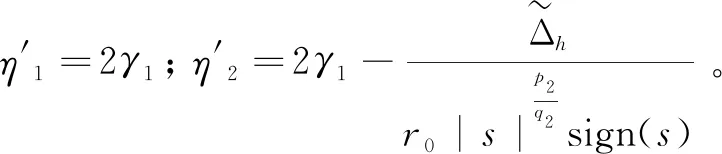
由式(20)可知，如果η1> 0，则式(20)的结构与式(5)类似。因此，保证了滑模变量s固定时间收敛。滑模变量s将在固定时间内收敛到以下区域

(21)

式(21)的分析与式(20)类似，可得滑模变量s将在固定时间内收敛到以下区域

(22)

|s|≤Ψs=min{Ψs1,Ψs2}

(23)

固定时间Tr=max{Tr1,Tr2}。

当非奇异固定时间收敛滑模变量s收敛到集合Ψs，需要对以下3种情况进行分析。

情况一：

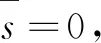
(24)

情况二：

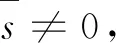
(25)

式(25)可以改写为

(26)

(27)

(28)

(29)

情况三：

(30)

综合情况一、情况二和情况三，可以得到当滑模变量s收敛到集合Ψs，状态x1和x2将在固定时间Ts内收敛区域，如式(31)所示。

(31)

因此，系统状态x1和x2将分别在固定时间内收敛到集合Ψx1和集合Ψx2，固定时间T=Tr+Ts，证明完毕。

4 数值仿真

本章通过数值仿真验证所提制导律的有效性。仿真场景为单一导弹对单一目标的拦截。导弹的初始位置xM=0 m，yM=0 m，速度vM=500 m/s；导弹航迹角θM=15°,30°,60°,90°,120°,150°；目标的初始位置xT=10 000 m，yT=10 000 m，速度vT=250 m/s，航迹角θT=180°；目标机动aT=8gsin(πt/10)，g=9.81 m/s2；期望终端视线角qd=40°；导弹的最大加速度20g。蒙特卡洛仿真条件：假设导弹的初始弹道角范围为15°～150°并服从均匀分布，导弹其他条件与上述情况一致，进行500次蒙特卡洛仿真。

制导律参数为：m1=n1=9/7,p1=q1=7/9,k1=0.2,k2=0.2，γ1=0.15,γ2=0.2，a1=0.8,b1=7,c1=2,ε=0.01。

图2～7分别给出了导弹和目标弹道、视线角、视线角速率、滑模变量、导弹过载、蒙特卡洛仿真结果。

图2 导弹和目标弹道Fig.2 Trajectories of missile and target

图3 视线角Fig.3 LOS angles

图4 视线角速率Fig.4 LOS angular rates

图5 滑模变量Fig.5 Sliding mode variables

图6 导弹过载Fig.6 Missile overloads

图7 蒙特卡洛仿真结果Fig.7 Monte Carlo simulation results

由图2可以看出，所设计制导律可以使得导弹在不同初始条件下均能成功拦截目标。由图3可以看出，在导弹不同初始条件下终端视线角可以在固定时间内收敛到期望值。由图4可以看出，在导弹不同初始条件下视线角速率可以在固定时间内收敛到零，固定时间约为15 s。图5可以看出，所设计的滑模变量在导弹不同初始条件下可以在固定时间收敛到零，固定时间约为10 s。图6可以看出，导弹的过载均在最大允许范围内，且在末制导段不存在由于目标机动引起的抖振和峰值现象。图7可以看出，导弹在不同初始条件下对目标拦截的脱靶量均小于0.6 m。因此，本文提出的制导律在不考虑初始系统状态的一定条件下，可实现制导系统状态和滑模变量固定时间收敛，对未知机动目标具有强鲁棒性，并且在终端角约束条件下可以精确地拦截目标。

5 结束语

本文提出了一种固定时间收敛的终端角约束滑模制导律，可以实现闭环制导系统在固定时间内稳定，并且闭环制导系统收敛时间的上界在一定条件下与制导系统初始状态无关。通过采用固定时间扰动观测器对集成不确定性进行补偿，导弹加速度不存在由机动目标引起的抖振和峰值现象。通过大量的数值模拟，对所提出的制导律进行了性能检验。所提制导律可以实现对不同初值制导系统的固定时间收敛，对未知目标机动具有强鲁棒性和较高的制导精度及较小的视线角跟踪误差。