动基座对准机翼挠曲变形补偿方法研究

李云龙，宋振华，刘伟鹏，张 进，冯 辉

(上海机电工程研究所，上海 201109)

0 引 言

在动基座对准研究中，为了对某一特定匹配方法的有效性进行研究，往往假设运载体是绝对刚体[1]，在机动对准过程中，主、子惯导之间不发生挠曲变形，但在实际中这一假设不能成立。例如载机在进行机动动作时，由于机翼上受到气动力和阵风的影响[2]，载机机翼会产生挠曲变形，这种挠曲变形往往有1°左右，严重影响了动基座对准的性能[3]，如何消除机翼挠曲变形对传递对准的影响是传递对准实现的关键。文献[4]通过放大系统噪声的方式来补偿机翼的挠曲变形，但要选取合适的系统噪声是十分困难的。文献[5]将机翼的挠曲变形描述为一个三阶Gauss-Markov过程，但这种方法设计的滤波器高达24维，严重影响了滤波的收敛速度，不适用于工程应用。文献[6]利用空气动力学理论、理论力学和材料力学理论建立了描述机翼挠曲变形的确定性模型，但这种模型的建立十分复杂，需要大量的计算和试验数据支撑，不适用于工程实现。本文基于对悬臂梁振动模型的分析，建立了描述机翼挠曲变形的二阶Gauss-Markov过程，并适当删减了滤波器的状态变量，大大减少了滤波计算量，所设计的挠曲变形补偿方法更适用于工程实现。

1 基于悬臂梁振动模型的挠曲变形角建模

机翼挠曲变形产生的主要原因是机动过程中机翼受到气动力和挂载导弹重力的作用发生振动[7]。将机翼视为悬臂梁，结合悬臂梁广义模态坐标下的振动模型[8]，可得机翼挠曲变形振型的物理模型为

(1)

式中：q(t)为机翼的广义坐标，是机翼沿机翼法向方向的偏移量；ξq为机翼的弯曲模态阻尼系数；ωq为机翼的弯曲模态频率；f(t)为机翼当前时刻所受的广义力，对于机翼来说主要是气动力和挂载导弹的重力；M为机翼的广义质量。

同一时刻，机翼上一点的弯曲变形大小与它在机翼轴向上的位置x有关，机翼弯曲运动与位置坐标之间的关系为

p(x)=cosh(βx)-cos(βx)+C1(sinh(βx)-sin(βx))

(2)

式中：p(x)为机翼弯曲位移量与位置坐标的关系；β是机翼结构特性的固有参数，与机翼自由弯曲振动圆频率、机翼抗弯刚度、机翼线质量有关；C1为比例常数。

根据机翼弯曲模型及其与位置坐标的关系，由模态叠加法可以得到每一时刻，某一固定位置的机翼弯曲物理坐标为

(3)

式中：pi(x)为各阶模态下机翼弯曲位移量与位置坐标的关系；qi(t)为各阶模态下机翼广义坐标下的振动模型。

对于机翼的挠曲变形，影响传递对准性能的主要为机翼的一阶振动[5]，对式(3)取一阶模态进行叠加，表达式为

γ(x,t)=p(x)q(t)

(4)

将式(4)左右两边分别对x求偏导，即可得到每一时刻，某一固定位置的机翼挠曲变形角度

(5)

如果知道了上面分析过程中的各个参数变化模型，那么就可以对机翼的动态变形角进行非常精确的补偿。但是在实际过程中，载机机翼的很多信息都无法获得，因此理论的物理模型在这里难以建立。

分析式(1)，可以看出机翼挠曲变形振型的物理模型和二阶Gauss-Markov过程十分相似，二阶Gauss-Markov过程描述为

(6)

式中，w为系统噪声。

假设由机翼挠曲变形引起的子惯导相对于主惯导挠曲变形角为

(7)

挠曲变形角速度为

(8)

认为三轴挠曲变形角是相互独立的[9]，则挠曲变形角的二阶马尔可夫过程模型为

(9)

式中：i=x,y,z;wλi表示均值为0，方差为Q的系统驱动白噪声；βi=2.146/τi为模型参数，τi为系统的相关时间，可以视具体载体情况而定。

由于三轴挠曲变形角是相互独立的，下文中仅对其中一轴的变形角进行分析，省略了相关符号的下标。

二阶马尔可夫过程离散化后的形式为

λk=aλk-1+bλk-2+Twk

(10)

式中：wk表示均值为0，方差为TQ的驱动白噪声。由自动控制原理[10]的相关知识可得，wλ的方差Q与挠曲变形角方差Dλ之间存在如下关系：

(11)

因此,在得知挠曲变形角方差Dλ和相关时间τi后，即可确定该随机过程的相关参数。下面分析离散化的挠曲变形角模型的具体表达形式。

(12)

进行连续系统的离散化处理，取系统的一阶状态转移矩阵

(13)

则式(12)的离散化形式为

(14)

消去中间变量ωk，可得

λk+1=2(1-βT)λk-(1-βT)2λk-1+Twk-1

(15)

式(15)即为离散形式的机翼挠曲变形角模型。设二阶随机过程相关时间为τ=5 s，方差强度为Dλ=9′，所形成的机翼挠曲变形角如图1所示；相关时间为τ=50 s，方差强度为Dλ=9′，所形成的机翼挠曲变形角如图2所示。针对高频振动的战斗机机翼，可以选取较小的相关时间和较大的方差强度来描述机翼挠曲变形。

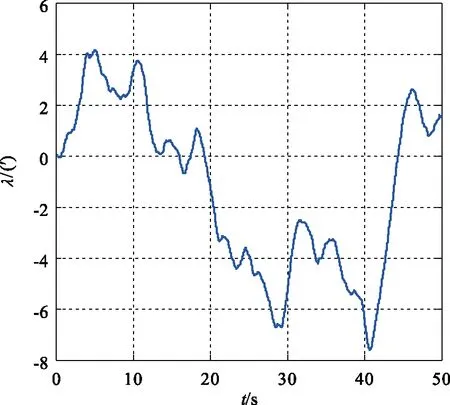
图1 相关时间为5s的挠曲变形角Fig.1 Deflection angle with correlation time of 5 seconds

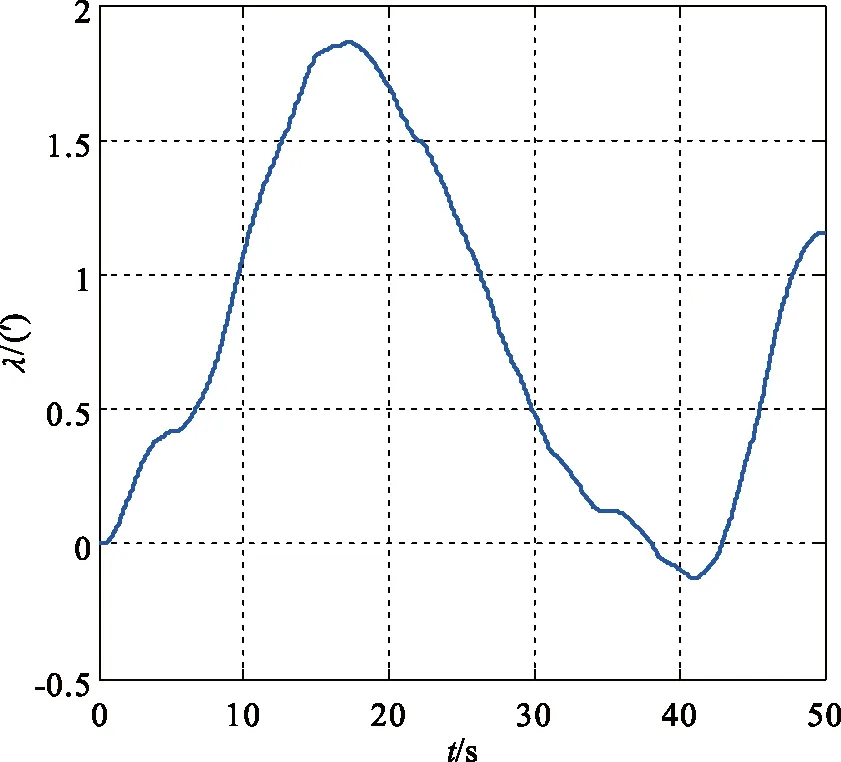
图2 相关时间为50s的挠曲变形角Fig.2 Deflection angle with correlation time of 50 seconds

2 机翼挠曲变形补偿方法

在第1章中，利用二阶随机过程模型对机翼动态挠曲变形角进行了建模，下面将研究如何使用建立的模型对机翼挠曲效应进行补偿。采用的方法是将挠曲变形模型的相关状态量引入到传递对准滤波器中，对机翼挠曲变形角进行估计补偿。

在传统的“速度+姿态”传递对准滤波器[11]状态量中加入挠曲变形角λ和挠曲变形角速度ω，系统状态变量为

(16)

式(16)所示滤波器的维数达到21维，严重影响了滤波速度，在工程实现上会遇到较大困难。由于捷联惯导系统的天向通道是发散的[12]，所以状态量中可以去除天向速度。由于机载战术武器所使用的陀螺仪和加速度计精度一般较高，而传递对准过程一般持续10 s以内[13]，在短时间内陀螺仪和加速度计零偏对于姿态和速度的影响很小，所以状态量中可以去除惯性器件的零偏。载机在机动过程中，由于机翼机械结构的关系，机翼挠曲变形多发生在沿载机x轴的方向，即λx对于对准过程影响最大，而λy和λz很小，对于对准过程的影响也很小，所以状态量中可以去除与λy和λz相关的状态量。对滤波器估计状态量进行简化删减后，“速度+姿态”传递对准滤波器状态量为

(17)

删减后的滤波器状态变量为10维，便于在工程实现中应用。“速度+姿态”对准滤波器的数学模型为

(18)

式中：A为系统状态转移矩阵；w为系统状态噪声；Z为系统观测量；H为系统观测矩阵；v为系统观测噪声。

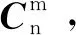
(19)

式中，[u×]和[λ×]分别表示固定安装误差角u和挠曲变形角λ构成的反对称矩阵。

3 仿真分析

第2章给出了机翼挠曲变形的补偿方法，本章基于传递对准滤波仿真，对该补偿方法进行仿真验证。针对通过补偿系统噪声来补偿机翼挠曲变形的方法和本文中所建立的挠曲变形补偿方法，对比了在机翼发生挠曲变形时两种方法对主、子惯导失准角的滤波效果。针对是否删减滤波器状态量，对比了传统21维滤波器和删减后的10维滤波器对主、子惯导失准角的滤波效果。仿真条件如下：

假定载机主惯导无误差，子惯导陀螺仪的常值零偏εb=2(°)/h，随机零偏εr=2(°)/h；子惯导加速度计的常值零偏b=400 ug，随机零偏r=400 ug；载机初始位置为经度108°，纬度34°，高度3 000 m处；载机初始速度为单位为m/s；采样周期和滤波周期均为0.01 s；设置的挠曲变形角相关时间为5 s，变形角方差为Dλ=9′；主、子惯导三轴固定安装误差角为在机翼发生挠曲变形时，分别对传统补偿系统噪声法和本文建立的挠曲建模补偿法进行仿真，仿真结果如图3～5所示。

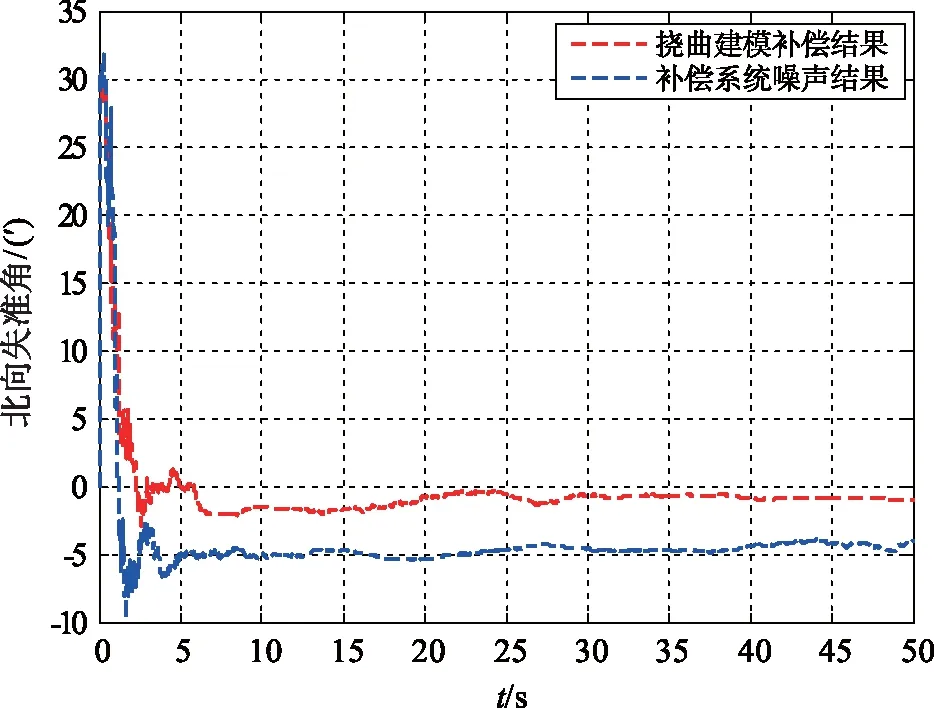
图3 滤波估计的北向失准角曲线Fig.3 North misalignment angle curve of filtering estimation

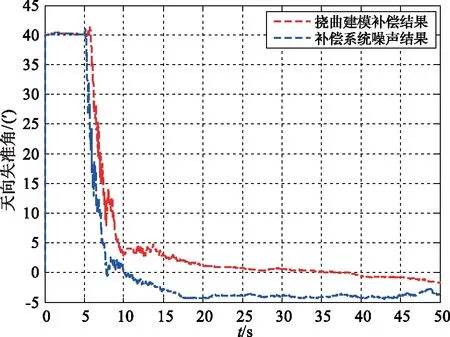
图4 滤波估计的天向失准角曲线Fig.4 Up misalignment angle curve of filtering estimation

图5 滤波估计的东向失准角曲线Fig.5 East misalignment angle curve of filtering estimation

由图3～5的仿真结果可以看出，在载机机翼发生挠曲变形时，传统的通过补偿系统噪声来补偿机翼挠曲变形的方法对于子惯导三轴失准角的估计效果较差，北向、天向失准角的估计误差为5′左右，东向失准角误差为3′。而本文建立的挠曲变形补偿方法对于子惯导北向和天向失准角估计误差均在2′以内，东向失准角在1′以内。仿真结果表明，本文建立的挠曲变形补偿方法比传统补偿系统噪声的方法更适用于机翼发生挠曲变形的动基座对准中。

滤波器对x轴挠曲变形角λx的估计结果如图6所示。

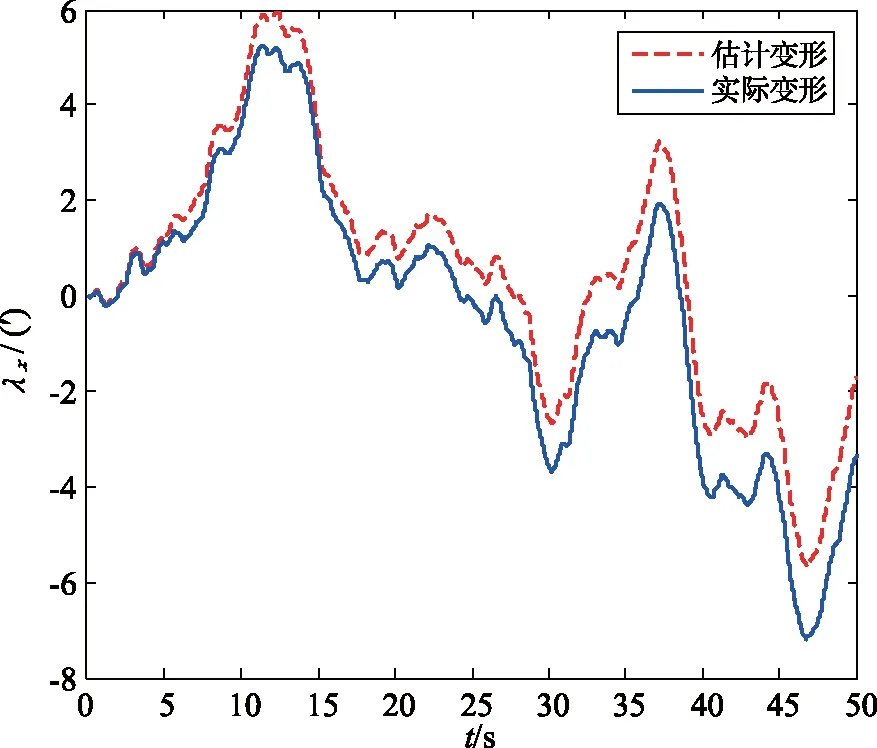
图6 x轴挠曲变形角跟踪曲线Fig.6 X-axis deflection angle tracking curve

由图6的仿真结果可以看出，滤波器对挠曲变形角的实时估计效果较好，可以有效跟踪系统所用的二阶随机过程模型。因此，将挠曲变形的随机过程模型引入传递对准滤波器中进行估计是可行的，并且这种方法可以有效降低机翼挠曲变形角对滤波器滤波性能的影响。

对删减状态变量前的21维滤波器和删减后的10维滤波器进行仿真对比，仿真结果如图7～9所示。

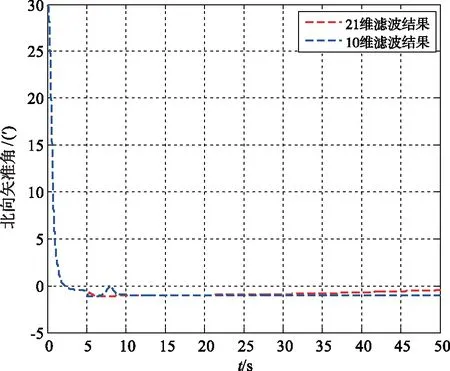
图7 滤波估计的北向失准角曲线Fig.7 North misalignment angle curve of filtering estimation

图8 滤波估计的天向失准角曲线Fig.8 Up misalignment angle curve of filtering estimation

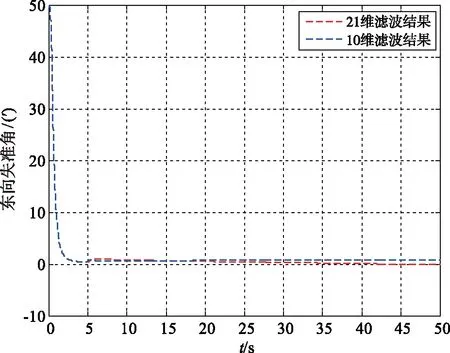
图9 滤波估计的东向失准角曲线Fig.9 East misalignment angle curve of filtering estimation

由图7～9的仿真结果可以看出，传统21维滤波器对子惯导北向、天向和东向失准角的估计误差均在1′以内，删减状态量的10维滤波器对子惯导三轴失准角的估计误差均在2′以内。相比较于21维滤波器，10维滤波器对子惯导失准角的滤波性能并没有受到太大影响。由文献[15]可知，滤波过程中存在矩阵求逆的过程，因此滤波器计算量与滤波维数的3次方成正比，那么21维滤波器的计算量大约为10维滤波器的9倍。10维滤波器通过删减合适的系统状态量，大大减少了滤波器计算量，滤波性能也没有受到太大影响，更适合应用于工程实现中。

4 结束语

本文针对机载武器动基座对准过程中的机翼挠曲变形，使用二阶随机过程模拟机翼的悬臂梁振动模型，对机翼挠性变形角进行建模，并将随机过程模型引入传递对准滤波器中进行补偿校正。仿真结果表明，该二阶随机过程模型能够很好地补偿机翼柔性变形对滤波器性能的影响，滤波器也可以对所使用的二阶模型进行很好的估计和跟踪，可以用来补偿机翼挠曲变形。另外通过对传统滤波器状态变量进行简化，所设计的“速度+姿态”滤波器计算量大大减少，且滤波精度并没有受到影响，更适用于工程实现。