基于飞行器三维组网测距信息的导航误差估计技术研究
张京娟,雷昊东,王学运,秦 峰
(1. 北京航空航天大学仪器科学与光电工程学院,北京 100191; 2. 北京航空航天大学合肥创新研究院,安徽 合肥 230012; 3. 上海机电工程研究所,上海 201109)
0 引 言
在现代社会中,卫星导航定位系统有着十分重要的地位,但是,由于战争环境复杂多变,平时可用于飞行器导航的全球卫星导航定位系统信号变得及其不稳定,容易遭到干扰或屏蔽[1]。相对而言,惯导系统具有不受外界干扰的优势,但其导航误差会随时间发散,长时间工作情况下导航定位精度不能得到保障。如何在无卫星导航定位系统情况下提高惯导系统的导航定位精度一直是研究的热点[2-4]。
在利用数据链提高组网飞行器的惯导系统导航定位精度方面[5-11],文献[5]研究了导航的协同定位技术,进行了在领弹指挥下的直线飞行仿真;文献[6]研究了利用数据链及最小二乘法提高两个无人机间的协同相对定位精度问题;文献[8]研究了以机载数据链和惯导系统为核心的二维平面机群组网协同定位技术,进行了二维平面内的仿真飞行实验;文献[9]研究了诱饵导弹通过伪距测量,利用卡尔曼滤波器得到自身的精确相对位置问题,诱饵导弹的定位需要领弹作为中心节点;文献[10]研究了通过迭代最小二乘法用估计值对量测方程模型误差进行补偿的方法,进行了30s仿真飞行,飞行器需做较大范围的相对机动;文献[11]提出了一种分层式协同导航系统方案,以僚机惯导输出误差作为状态量,利用相对导航与长/僚机惯导信息构造量进行测量,通过卡尔曼滤波估计出僚机的惯导误差。现有研究主要针对组网内部有中心节点的情况并且在二维平面内进行研究。本文针对无卫星导航定位系统情况,当组网内包含多个飞行器时,利用飞行器间测距信息进行三维组网的导航误差估计技术研究。系统无需中心节点,即使数据链失效使组网节点个数发生变化,系统依然能够正常工作,大幅提高其在实际应用中的可靠性。
1 基于测距三维组网导航的技术方案
1.1 基本原理
首先,通过数据链测量三维组网各飞行器之间的相对距离并互相通报各自的惯导位置信息和相互之间的测距信息;然后,利用相互测距值与计算距离(由惯导位置信息计算得到的飞行器间距离)之差作为量测量估计各节点的惯导位置误差,就可以达到类似于将“加权平均”思路应用于三维组网的效果。这就是基于飞行器三维组网测距信息的导航误差估计技术的基本原理。
为了进一步提高惯导系统的导航定位精度,可以在飞行器三维组网中设置一个具有高精度组合导航设备的校正站。该校正站可首先利用高精度组合导航系统确定精确的位置信息,然后将其与三维组网内部飞行器之间的测距值和其与组网内部飞行器之间的计算距离之差作为量测量,将该量测量作为基于飞行器三维组网测距信息的导航误差估计算法量测方程的一部分,对惯导系统的位置误差进行修正。这就是内部包含高精度组合导航校正站的基于飞行器三维组网测距信息的导航误差估计技术的基本原理。
基于飞行器三维组网测距信息的导航误差估计技术在卫星导航定位系统不可用时,在不改变单个飞行器的惯导系统的情况下,可实现提高导航定位精度的效果,而且能够同时提高多个飞行器的导航定位精度。
1.2 技术方案
基于飞行器三维组网测距信息的导航误差估计技术的实现要依托基于飞行器三维组网测距信息的导航误差估计系统,因此有必要研究系统的设计方案,分析所涉及的关键问题。
三维组网中的每个飞行器被称为一个节点,每个节点的组网导航系统都由一套数据链、一套惯导系统以及一套计算机组成。
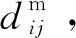
当组网中包含一个高精度组合导航校正站时,该校正站也配置有数据链设备,通过数据链设备完成其与组网飞行器之间的通信和测距。
1.3 导航效果评估指标
对于飞行器三维组网,要评估基于飞行器三维组网测距信息的导航误差估计技术的组网导航效果,有必要给出组网导航效果的评估指标和方法。
可以设定两个指标来评估飞行器三维组网导航效果:一个是三维组网导航后组网的导航定位精度r′(即修正后的组网导航定位精度,可以称之为“组网导航定位精度”);另一个是组网导航后组网导航定位精度的倍数Rimprove。
因此,三维组网导航定位精度r′可以表示为
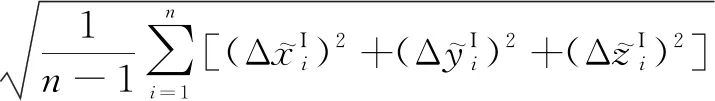
(1)

三维组网导航定位精度的倍数Rimprove可以表示为
(2)
式中,r是组网导航定位修正前的三维组网导航定位精度,可以表示为

(3)

2 导航误差估计算法


(4)
式中,Δij为测距值的误差,Δij~N(0,σr2),σr2为测距值方差。

(5)
(6)

(7)
因此,通过数据链得到的各飞行器间“测距距离”与通过惯导系统得到的各飞行器间“计算距离”之差作为三维组网导航的观测量,可以表示为
(8)

(9)
(10)
将式(8)写成矩阵形式,可表示为
L=HX+Δ
(11)

考虑量测值随机性质,可以得到三维组网导航系统的数学模型为
(12)


(13)
由于仅根据“测距距离”和“计算距离”之差还不足以确定组网在三维空间中的绝对位置,因此H不满秩。

(14)
式中:PX为根据各惯导系统精度水平确定的待估参数向量X的3n×3n维权阵,表达式为
(15)
GT是由HTPH的零特征值对应的特征向量组成的6×3n维矩阵,即GT同时满足
(16)
式中,rank (·) 为矩阵的行秩,针对不同的惯导系统需要设置不同的GT参数。
(17)


(18)

(19)


(20)

将式(5)代入式(20)并线性化,得

(21)

(22)

Lw=HwX+Δw
(23)

结合式(11)和式(23),可以得到含有高精度组合导航校正站的基于飞行器三维组网测距信息的导航误差估计技术的量测方程,为
(24)
令[L,Lw]T=L*,[H,Hw]T=H*,[Δ,Δw]T=Δ*,则式(24)可以写为
L*=H*X+Δ*
(25)

式(25)即为含有高精度组合导航校正站的飞行器三维组网导航系统的数学模型,下面对该数学模型进行求解。
式(25)的系数矩阵仍然不满足列满秩,所以还需要为方程增加新的求解条件。因此,含有高精度组合导航校正站的飞行器三维组网导航技术的解算模型为
(26)
式中:V*为Δ*的估计值;P*为量测矩阵L*的(n+p)×(n+p)维权阵;PX为根据各惯导系统精度水平确定的待估参数向量的3n×3n维权阵,如式(27)所示。
G*T是由H*TP*H*的零特征值对应的特征向量组成的矩阵,通过对G*T选取合适的典型值,进行解算,可得
(28)
3 仿真验证
3.1 组网由纯惯导设备飞行器组成
仿真条件1:飞行器三维组网节点数为4,分别编号为节点1~4;开始时刻,各飞行器在相邻节点间距离为60 km的相同高度正方形平面上分布,组网飞行器飞行高度为7 km,组网飞行器先北飞后东飞,航速为200 m/s,航向角ψ为 0°,飞行器数据链测距误差为20 m;节点1~4的惯导系统的陀螺随机常值漂移均为3 (°)/h,加计随机常值零偏为8×10-4g;开始时刻,节点1~4的惯导系统的定位误差为30 m。飞行器飞行轨迹如图1所示。

图1 飞行器飞行轨迹(仿真条件1)Fig.1 Aircraft flight trajectory (simulation condition 1)
仿真结果:当三维组网内有4个纯惯导设备飞行器时,飞行器飞行10 min后,修正前导航误差为13 796.82 m,修正后导航误差为5 881.69 m,修正后组网导航定位精度提高了1.345 7倍。修正前后导航位置误差变化曲线如图2所示。

图2修正前后导航位置误差(仿真条件1)Fig.2 Navigation position errors before and after correction (simulation condition 1)
3.2 组网内含一个高精度导航校正站
仿真条件2:三维组网中包含4个飞行器和1个高精度组合导航校正站(校正站水平方向距离正方形中心480 km,高度7 km,位于飞行器组网初始航向上),4个飞行器编号为节点1~4;其余条件同仿真条件1。飞行器飞行轨迹如图3所示。
仿真结果:当三维组网内为4个纯惯导设备飞行器与1个固定位置高精度组合导航校正站时,飞行器飞行10 min后,修正前误差为15 765.95 m,修正后误差为1 350.05 m,修正后导航定位精度提高了10.678 倍。飞行过程中修正前三维组网、纯惯导组网修正后及校正站修正后导航误差变化曲线如图4所示。

图3 飞行器飞行轨迹(仿真条件2)Fig.3 Aircraft flight trajectory (simulation condition 2)

图4 修正前后导航位置误差(仿真条件2)Fig.4 Navigation position errors before and after correction (simulation condition 2)
4 结束语
本文针对无卫星导航定位系统条件下惯导系统导航误差随时间发散问题,提出了一种利用测距信息的飞行器三维组网导航方法以提高惯导系统导航定位精度。该技术通过数据链得到飞行器间测距信息,再结合各节点的惯导信息估计各套惯导的位置误差,设计三维组网导航误差估计算法,并对算法进行了仿真验证,仿真结果表明:基于飞行器三维组网测距信息的导航误差估计技术能够对飞行器的惯导误差进行修正,有效减缓惯导位置误差发散的速度,从而提升了飞行器三维组网的导航定位精度。

