随机强伪压缩算子多步迭代序列的收敛性

聂 辉，张树义

（渤海大学 数理学院，辽宁 锦州121013）

1 引言和预备知识

随机不动点问题广泛应用于生物、物理和经济等领域.文献[1-8]对随机不动点理论进行了广泛研究，其中，文献[1-2]在可分的Hilbert空间中研究了随机算子方程解和随机算子不动点随机Mann迭代序列的收敛性，文献[3]在值域有界的一致光滑可分的Banach空间中研究了一类随机强伪压缩算子随机不动点的Ishikawa迭代序列的逼近问题.另外，文献[9-17]研究了包括广义Lipschitz算子在内的几类非线性算子不动点迭代的逼近问题，文献[18-24]研究了几类非线性映象不动点多步迭代算法的收敛性.受上述工作启发，本文用广义Lipschitz取代值域有界条件，在可分Banach空间中研究一类随机强伪压缩算子随机不动点的多步随机迭代序列的逼近问题，建立了随机强伪压缩算子随机不动点的多步随机迭代序列的强收敛性定理.由于值域有界一定是广义Lipschitz的，而反之未必成立[13]，因此本文推广和改进了相关文献中的结果.

假设（Ω，∑）为一可测空间，∑是Ω的σ-代数.E为一致光滑的可分Banach空间，E*为E的对偶空间，C为E的非空闭凸子集，正规对偶映象J：E→2E*为

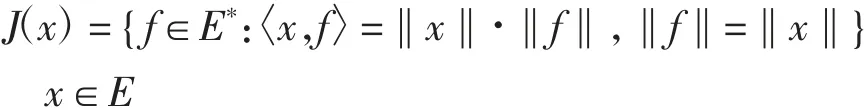
定义1[3]（1）称函数f：Ω→C为可测的，如果对任意Borel子集B，有f-1（B∩C）∈∑.

（2）称T：Ω×C→C为随机算子，如果对任一x∈C，T（·，x）：Ω→C是可测的.

（3）称可测函数f：Ω→C为随机算子T：Ω×C→C的随机不动点，如果对任意ω∈Ω，有T（ω，fω）=f（ω）.

（4）称随机算子T：Ω×C→C为连续的，如果对任意给定的ω∈Ω，T（ω，·）：C→C是连续的.

引理1[8]设E为可分的距离空间，Y为距离空间.T：Ω×E→Y在ω∈Ω是可测的，并且在x∈E是连续的.如果g：Ω→E是可测函数，则f（·，g（·））：Ω→Y是可测的.

定义2设Ti（i=1，2，…，s）：Ω×C→C为s个连续的随机算子，x0：Ω→C是任意给定的可测函数，定义序列{xn（ω）}为

称序列{xn（ω）}为随机多步迭代序列，其中[0，1]，i=1，2，…，s-1.

在定义2中取s=2，对每一ω∈Ω，令T1（ω，·）=T2（ω，·）=T（ω，·），便得到文献[10]中的随机Ishikawa迭代序列

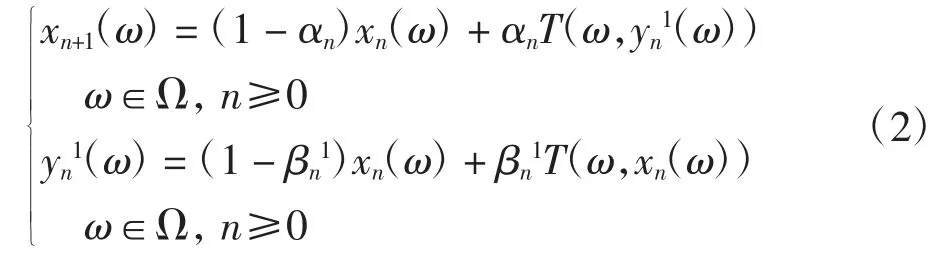
注1Ti（i=1，2，…，s）：Ω×C→C是连续的随机算子，C是E的非空闭凸子集，x0：Ω→C是可测函数.由引理1易知{xn}和{yni}（i=1，2，…，s-1）是Ω到C的可测函数.

定义3[3]（1）称随机算子T：Ω×C→C为强伪压缩的，如果存在函数k：Ω→（0，1），对任意x、y∈C，存在j（x-y）∈J（x-y），使得对每一ω∈Ω，有

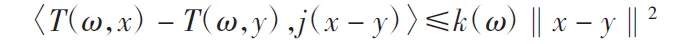
（2）称随机算子T：Ω×C→C为强增生的，如果存在函数h：Ω→（0，1），对任意x、y∈C，存在j（x-y）∈J（x-y），使得对每一ω∈Ω，有

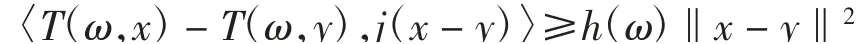
注2T：Ω×C→C是具有函数k：Ω→（0，1）的强伪压缩算子，当且仅当I-T是具有函数h：Ω→（0，1）的强增生算子，其中h（ω）=1-k（ω）.

下面将广义Lipschitz算子扩展到随机算子的情形.

定义4称随机算子T：Ω×C→C为广 义Lipschitz的，如果存在常数L≥1，使得对任意x、y∈C，对每一ω∈Ω，有

注3文献[13]指出：值域有界的随机算子一定是广义Lipschitz的，而反之未必成立.

引理2[9]设E为实Banach空间.

（1）如果T：E→E是连续的强伪压缩算子，则T有唯一不动点.

（2）如果T：E→E是连续的强增生算子，则对f∈E，方程Tx=f有唯一解.

引理3[3]设E为实Banach空间，J是正规对偶映射，则对任意x、y∈E，有

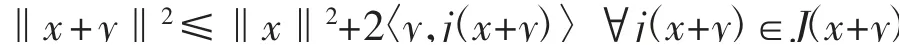
引理4[10]设{an}和{bn}为2个非负实数列，满足an+1≤（1-tn）an+bn，n≥n0，其中n0是非负整数，tn∈则有

2 主要结果

定理1设E为实一致光滑可分的Banach空间，C是E的非空闭凸子集，Ti（i=1，2，…，s）：Ω×C→C是具有函数k：Ω→（0，1）的s个连续广义Lipschitz随机强伪压缩算子，Ti（ω，·）的不动点集记为F（Ti（ω，·）），是由式（1）定义的多步随机迭代序列满足条件则序列{xn}强收敛到Ti的随机公共不动点.

证明因为Ti（i=1，2，…，s）：Ω×C→C是具有函数k（ω）：Ω→（0，1）的连续随机强伪压缩算子，任意给定ω∈Ω，Ti（ω，·）：C→C是具有k（ω）∈（0，1）的强伪压缩算子，由引理2知Ti（ω，·）：C→C有唯一不动点，即存在唯一的xi*（ω）∈C，使得xi*（ω）=Ti（ω，xi*（ω））.又因此，对任意给定的ω∈Ω，存在唯一的由式（1），对每一ω∈Ω，有

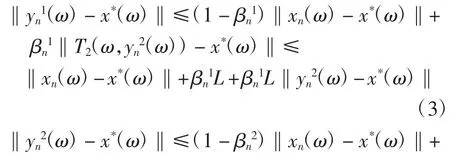
将式（4）代入式（3）可得

由式（1）连续做s-2步迭代，有

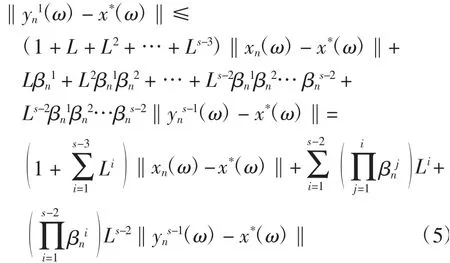
又由式（1）有

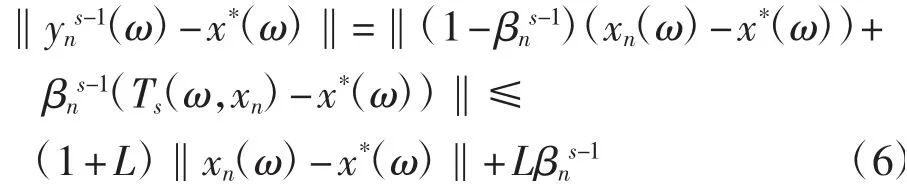
将式（6）代入式（5），可得对每一ω∈Ω，有

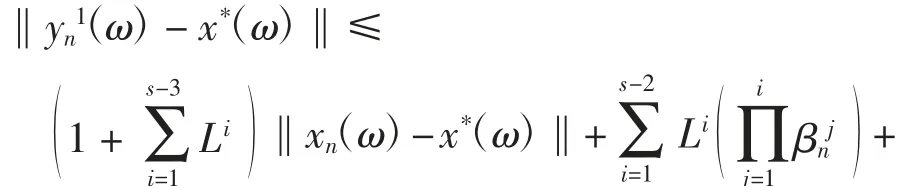
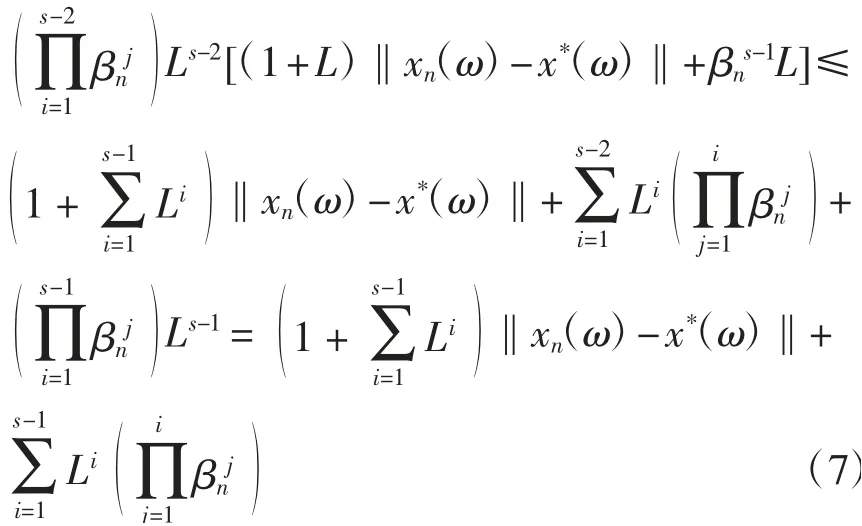
类似式（7）的证明过程可得

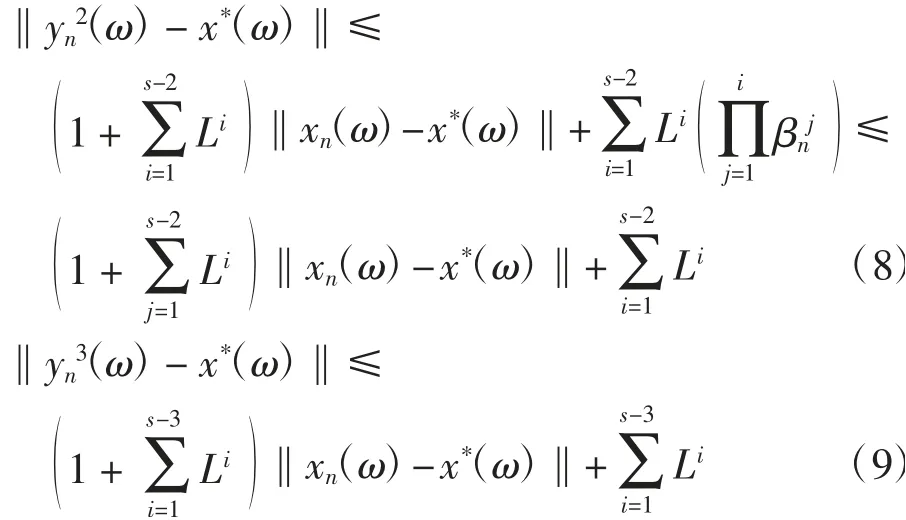
因为Ti：Ω×C→C是广义Lipschitz的，故存在常数L≥1，使得对任意x、y∈C及每一ω∈Ω，结合式（7）有

由式（1）和引理3，对每一ω∈Ω，有

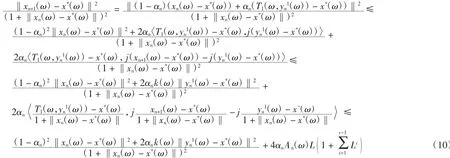
其中

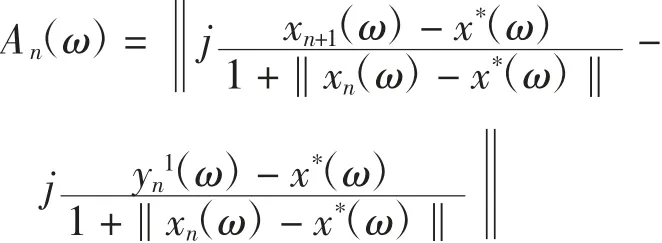
下证An（ω）→0（n→+∞）.由式（1）和式（8），对每一ω∈Ω，有

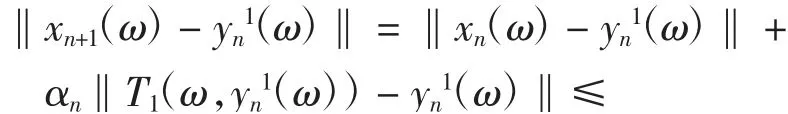
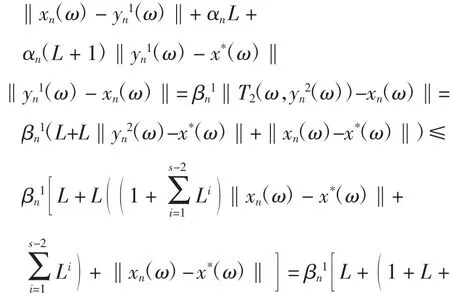
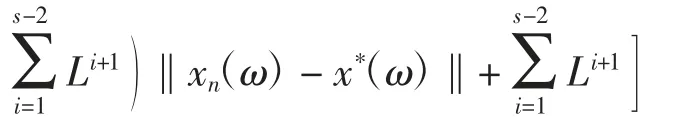
于是对每一ω∈Ω，有

因为E是一致光滑的Banach空间，故正规对偶映象J在E的任何有界子集上一致连续，于是由J的一致连续性可知：对每一ω∈Ω，有An（ω）→0（n→+∞）.

由式（1）和引理3以及式（8），对每一ω∈Ω，有

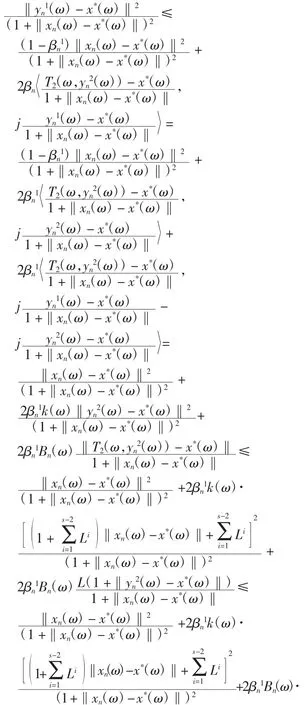
其中

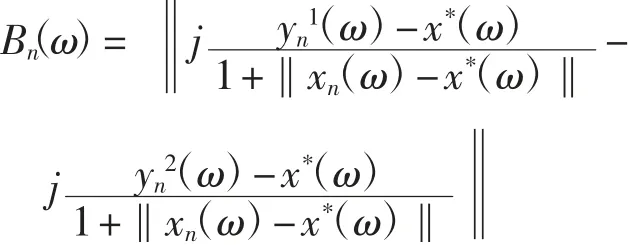
下证Bn（ω）→0（n→+∞）.由式（1），对每一ω∈Ω，有

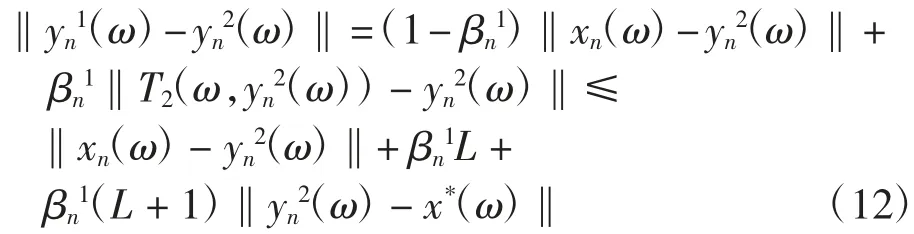
由式（1）和式（8），对每一ω∈Ω，有

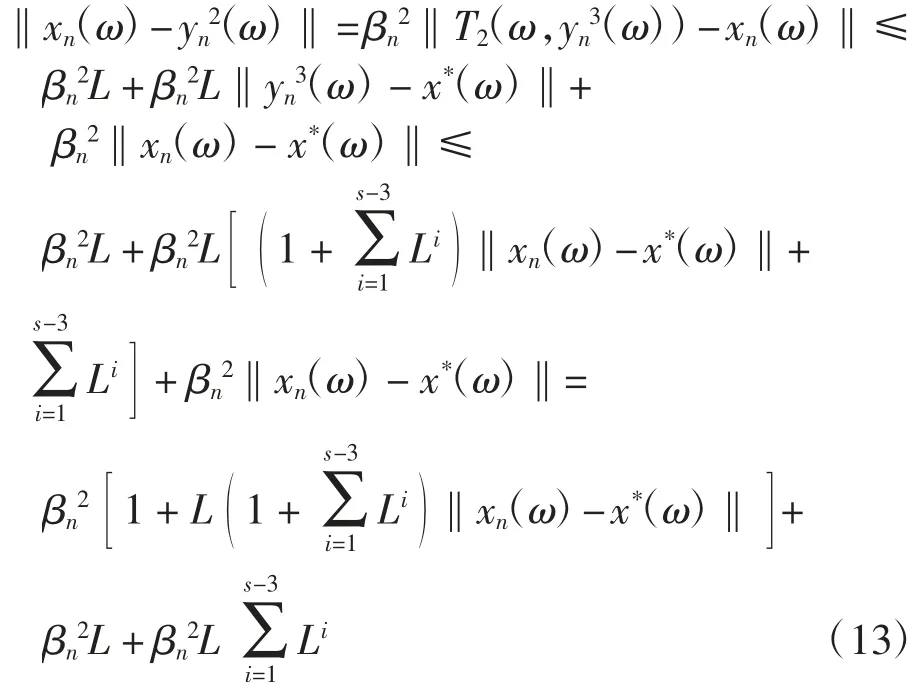
将式（8）和式（13）代入式（12），有

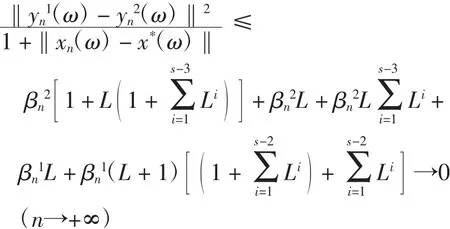
由J的一致连续性知Bn（ω）→0（n→+∞）.

将式（11）代入式（10），对每一ω∈Ω，有

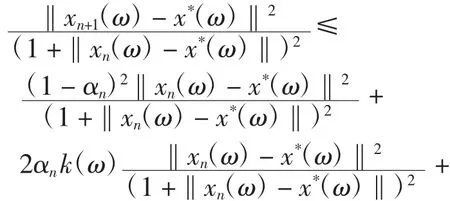
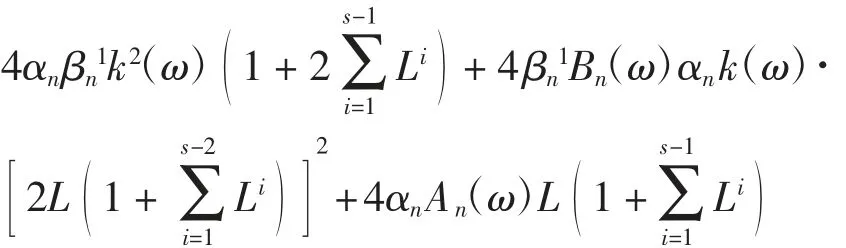
据此可得

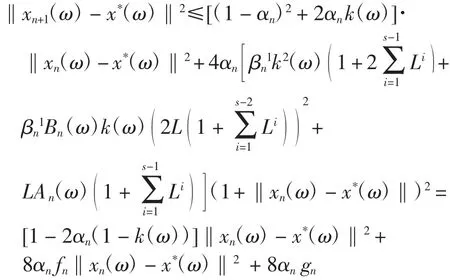
其中

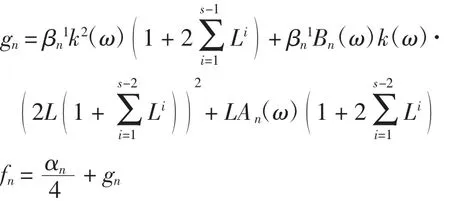
因为αn→0，gn→0（n→+∞），因此fn→0（n→+∞），于是存在正整数n0，对n>n0，有从而对任意n>n0，对每一ω∈Ω，有

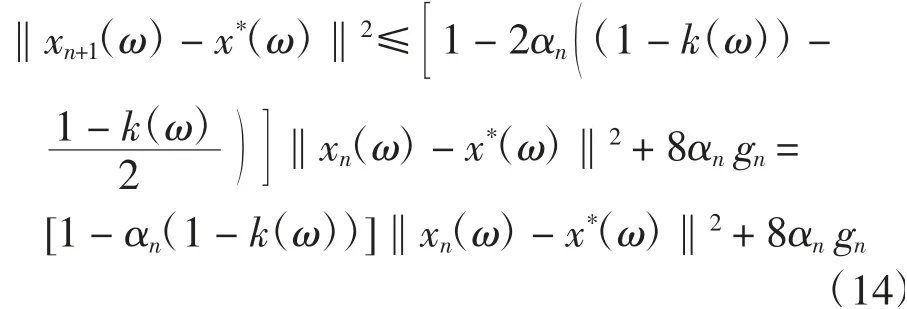
推论设E为实一致光滑可分的Banach空间，C是E的非空闭凸子集，T：Ω×C→C是具有函数k：Ω→（0，1）的连续广义Lipschitz的随机强伪压缩算子.{xn（ω）}是由式（2）定义的随机Ishikawa迭代序列.{αn}、{βn1}⊂[0，1]满足条件则序列{xn}强收敛到T的随机不动点.

作为上述结果的应用，下面讨论强增生随机算子方程随机解的迭代收敛性.

定理2设H为可分的Hilbert空间，T：Ω×H→H是具有函数h：Ω→（0，1）的连续随机强增生算子.设f：Ω→H为一可测函数，令S：Ω×H→H为S=IT+f.x0：Ω→C为任意给定的可测函数，{xn（ω）}是由下式定义的随机Ishikawa迭代序列，

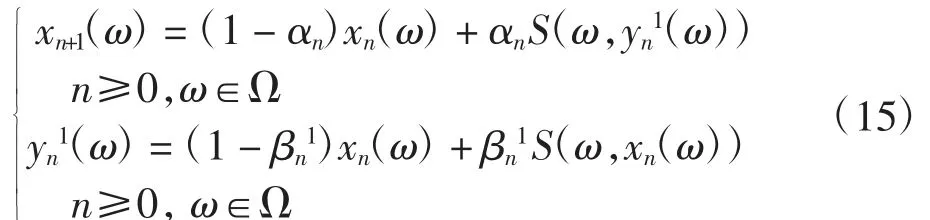
{αn}、{βn1}⊂[0，1]满足条件（1）αn→0，βn1→0（n→+∞）；如果S是广义Lipschitz的，则对任意给定的可测函数f：Ω→H，随机算子方程

有唯一随机解x*：Ω→H，且对每一ω∈Ω，随机迭代序列{xn（ω）}强收敛到x*（ω）.

证明由条件可知S：Ω×H→H是具有函数k：Ω→H，k（ω）=1-h（ω）的连续广义Lipschitz随机强伪压缩算子.由推论，对每一ω∈Ω，由式（15）定义的序列{xn（ω）}强收敛到S的随机不动点x*：Ω→H，因此S（ω，x*（ω））=x*（ω），即T（ω，x*（ω））=f（ω），ω∈Ω，这蕴含x*（ω）是随机方程（16）的随机解.证毕.

注4本文从两方面推广和改进了文献[3]中的结果：（1）将随机Ishikawa迭代序列推广到多步随机迭代序列；（2）用广义Lipschitz算子取代值域有界条件.

例设Ω=[0，1]，取C=（-∞，+∞）具有通常意义的范数.∑是Ω的σ-代数在[0，1]上的Lebesgue可测子集，定义随机算子T：Ω×C→C为T（ω，x）=2ω-x，则对每一ω∈Ω，可测映象x*：Ω→C，x*（ω）=ω是T的唯一随机不动点.对任意x、y∈C，存在j（x-y）∈J（x-y），使得对每一ω∈Ω，取有

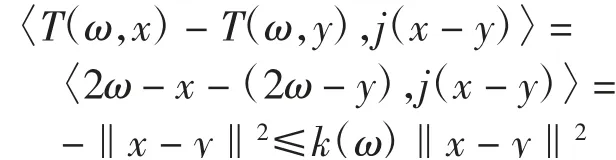
由此T：Ω×C→C是一个具有的强伪压缩算子，且是具有L=1的广义Lipschitz算子.取则推论中的所有条件均满足.因此由式（2）定义的序列{xn}强收敛到T的随机不动点x*（ω）=ω.事实上

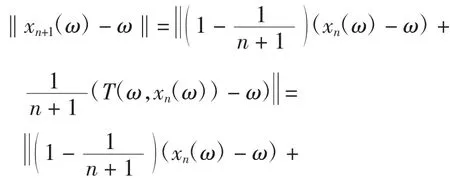
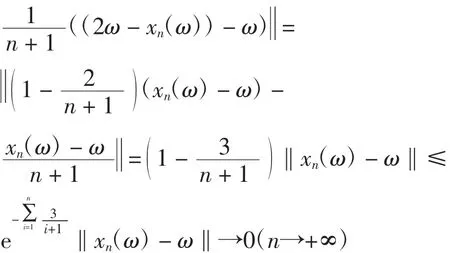
但因为T的值域无界，因此文献[3]中的定理2.1不能用于此算例.