高速工况下间接式胎压监测的影响因素研究与优化＊

彭加耕 王宇岱 韩宗奇 王振

（1.燕山大学，秦皇岛 066004；2.苏州绿安汽车科技有限公司，苏州 215200）

1 前言

轮胎是车辆唯一与路面接触的部分，胎压监测已成为汽车安全领域的一项重要功能[1]。间接式胎压监测系统（Tire Pressure Monitoring System，TPMS）采用的主要方法有轮速比较法[2]、轮胎扭转刚度法[3]、轮胎纵向刚度法[4]、频谱法[5]等。韩宗奇、王立强教授等基于轮胎的滚动半径对间接式TPMS 开展了研究[2]，对轮速传感器脉冲信号进行采样处理，即采用脉冲比较法，并在实车道路试验中取得了良好效果。

在间接式TPMS研发过程中，通过分析大量道路试验[6]数据发现，存在参数值随速度变化趋势分离的现象，即高速工况下前轮倾向于缺气误报，后轮侧向于缺气漏报，这也使间接式TPMS在高速行驶时无法有效监测轮胎气压。本文在脉冲比较法的基础上，借鉴轮胎纵向刚度法，基于CarSim 整车模型选用适合的轮胎模型对车辆行驶过程进行动力学分析，分析车辆高速行驶对间接式TPMS 参数的影响，并提出车速补偿方法，对间接式TPMS在高速行驶中的应用进行优化。

2 间接式TPMS监测原理

轮胎气压变化直接影响车轮的滚动半径，滚动半径的变化直接影响轮速的测量，可通过分析轮速信号反映车轮滚动半径的变化，进而完成对轮胎气压的监测[3]。脉冲比较法的理论基础为三均值比较法，将1个采样周期中某车轮的标准脉冲数与其他3 个车轮标准脉冲数平均值进行比较[7]。除第i轮外的其他3 个轮胎的标准脉冲数平均值为：

式中，SNi为对应车轮的传感器脉冲数统计值。

每个车轮的三均值脉冲差为：

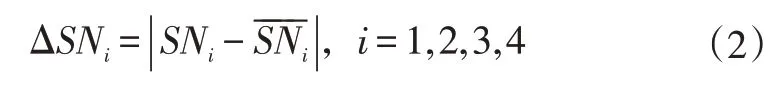
ΔSNi越大，该轮的气压异常程度越高，从而可实现轮胎气压异常的判断[8]。

在实际应用中，车辆高速行驶时，TPMS 监测结果波动较大，具体表现为：前轮轻度缺气易判定为气压不足，而后轮气压不足易判定为气压正常。对不同行驶速度下单轮缺气时4 个车轮的ΔSNi进行统计，结果如图1所示。

图1 不同车速下4个车轮单轮缺气的脉冲差

图1 中，ΔSN1～ΔSN4分别为对应缺气轮胎气压0.173 MPa，其他轮胎气压0.240 MPa时的统计值。可以看出，车速高于100 km/h 后，参数出现分离现象，这将影响TPMS 的正常监测功能。参数出现分离的直接原因是在高速工况下，驱动轮的转速大于从动轮转速且该趋势随车速的提高持续增大。在ABS 应用中也存在车轮的转速补偿问题[9]，但其主要应用于车辆制动过程。对于TPMS而言，在正常驱动过程中主要存在两方面因素，即轮胎滚动半径改变和车轮滑移率改变，后者可通过轮速信号直接反映出来。

3 车辆行驶动力学方程的建立

随着汽车技术的发展，汽车的行驶速度越来越快，空气动力对车辆行驶的影响也越来越重要。大量统计数据表明，当车速达到70 km/h左右时，汽车受到的空气阻力和滚动阻力几乎相等，当车速达到150 km/h 后，汽车所受的空气阻力是滚动阻力的2～3 倍[10]。在汽车高速行驶时，气动升力对汽车各性能的影响则更为明显。随着气动力的影响比重逐渐增大，车辆的纵向力与垂向力均受到明显影响，同时，车速的变化将影响轮胎的纵向力和垂向力分布。TPMS 通过对ABS 的轮速传感器信号脉冲数进行运算得到胎压间的相对关系，因此需要分析车辆在直线行驶过程中的纵向和垂向特性。

3.1 车辆纵向力学分析

汽车在实际行驶过程中受到的行驶阻力包括滚动阻力Ff、空气阻力Faero、爬坡阻力Fi和加速阻力Fj。由汽车驱动力平衡可得汽车所需驱动力F为：

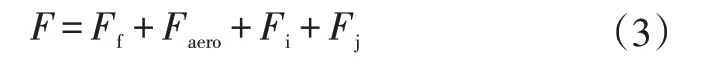
假定试验车辆在良好路面上正常行驶，前轮驱动，后轮自由滚动，对于轿车而言，车速不超过140 km/h 时滚动阻力Ff多在100 N以下[11]，可以忽略。

我国高速公路允许的最大纵向坡度在平原微丘地区为3%，山岭重丘地区为5%，本文重点研究车辆在高速工况下的参数分离现象，故爬坡阻力Fi在坡度较小且车辆自重较小时也可以忽略。根据实际车辆试验结果可知，爬坡阻力Fi在车辆低速行驶过程中会造成前、后轮脉冲数差异，但不会影响缺气判断，为提高胎压判断精度，可对低速阶段坡道工况进行修正。

根据实际车辆测试结果可知，起步加速和急减速工况对车轮脉冲数有较大影响，试验车辆为前驱车，具体表现为起步加速工况造成两前轮脉冲数增多，急减速工况两后轮脉冲数增多，且增多的脉冲数量与加、减速度存在线性关系，可引入加、减速参数对其进行修正。本文假设车辆在高速工况下不存在起步加速和急减速工况，故不考虑加速阻力的影响，则动力学方程可简化为：

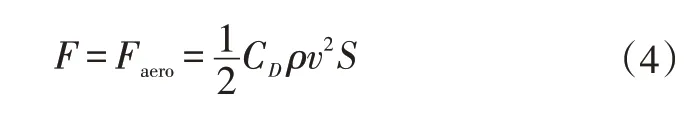
式中，CD为空气阻力系数；ρ为空气密度；v为车速；S为迎风面积。

3.2 车辆垂向力学分析

车辆在匀速行驶过程中，受到气动升力与空气阻力产生的俯仰力矩导致前、后轴载荷不同，进而导致轮胎的滚动半径发生变化。汽车垂向受力如图2所示。

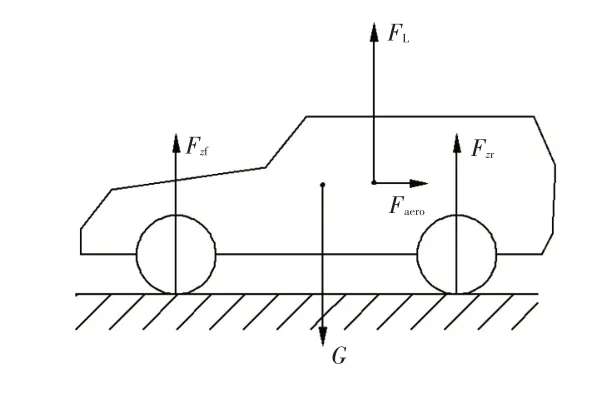
图2 汽车垂向受力示意

对作用于前轮接地中心的转矩进行分析可得：

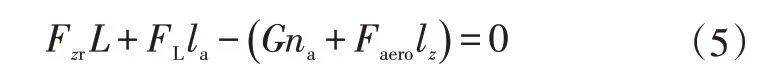
其中，后轴的垂向载荷Fzr为：

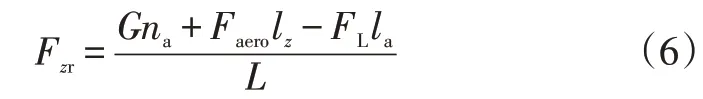
式中，G为车辆的重力；na为车辆重心至前轴的距离；L为轴距；la为风圧中心至前轴的距离；lz为风圧中心至地面的距离；为空气升力；GL为升力系数。

由车辆垂向力平衡可得到前轴的垂向载荷Fzf为：

高速工况下汽车受到的阻力加大，驱动轮需要更大的驱动力，导致其滑转率增大[12]，因此，在行驶距离相同时，驱动轮转过的圈数增加，导致滚动半径变小。

4 轮胎受力特性分析

制动过程的持续时间短暂，在TPMS监测过程中舍弃制动过程，仅对驱动工况进行研究。因此纵向力分析用于计算驱动轮、从动轮的滑转率，垂向力分析则用于观察轮胎滚动半径的真实变化情况。

4.1 轮胎模型的选择

在轮胎建模领域，研究者们进行了大量的探索，目前主要建立了经验模型和物理模型两大类模型[13]。Pacejka 等提出的魔术公式[14-15]、郭孔辉院士提出的幂指数统一模型[16]属于半经验公式，并广泛应用于轮胎仿真领域，且在纵向与侧向力联合工况下具有很好的效果[17]，但该类模型需要大量的试验数据，参数较多。对于TPMS，主要分析其驱动过程中的纵向运动受力，因此本文选用更加简化的刷子模型。

刷子模型作为一个简化物理模型，将轮胎看作由连接在刚性基座（轮缘）上的一系列可以产生伸缩变形的弹性刷毛组成，这些刷毛则承受垂向载荷以及轮胎受到的纵向力和侧向力。

轮胎接地区域长度为2a，当车轮滚动速度大于车轮平均移动速度时，刷毛接地端有“粘附于路面”的趋势，从而使刷毛单元产生形变，其两端产生速度差，如图3所示。假设车轮半径远大于接地区域长度，即r≫a，且刷毛单元足够小，以刷毛单元A-A′为例，相对于车轮中心，单元上端点A以速度ωr向后运动，下端点A′因地面附着作用以速度u运动，则刷毛单元沿x方向的纵向形变为ξ=(ωr-u)Δt。若以刷毛单元所处位置为自变量，则有：

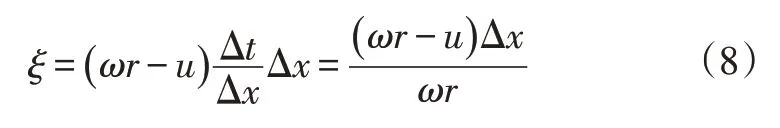
式中，Δx=a-x为带束层宽度；Δt为时间变化量；x为刷毛单元相对于带束层离开接地点的距离。

图3 刷子轮胎模型

在车辆驱动过程中，驱动轮的滑转率定义为：

假设产生的正比于刷毛单元纵向形变的单元弹性力Fex为：

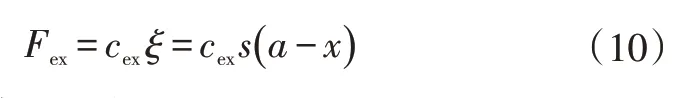
式中，cex为刷毛单元刚度。

因此，整个接触区域的轮胎纵向力Fx由积分得到：

当滑转率较小时，有ωr≈u，因而，轮胎纵向力Fx近似为：

式中，cs=2cexa2为轮胎纵向滑转刚度。

其中，轮胎气压的降低导致接地区域的扩大，即a增大，使得轮胎纵向刚度增大[18]，虽然垂向载荷的变化也导致a的改变，但对轮胎纵向刚度并无明显影响。

当达到或超过地面附着极限时，已不能用线性模型简单地进行纵向力估计。考察轮胎接地印迹内垂向载荷分布情况可知，接地印迹中心的轮胎垂向载荷Fz最大，中心前、后逐渐减小至零，因而可近似认为接地印迹内的垂向应力呈二次函数分布：

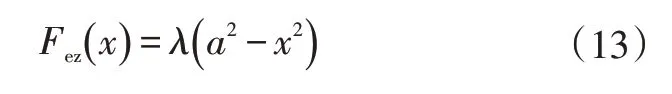
式中，λ为待定系数。

已知轮胎垂向载荷Fz，λ可由式（14）求解：

设地面附着系数为μ，每一单元的最大纵向力Fex≤μFez，结合式（11），可将接地区域分为两部分，前部为附着区，后部为滑转区，长度为d=|a|-|xA|=cex/(μλ)，其中xA=cex/(μλ)-a为临界点坐标。

因此可得到整个接地印迹的纵向力为：

得到滑转率曲线和纵向力曲线如图4所示。

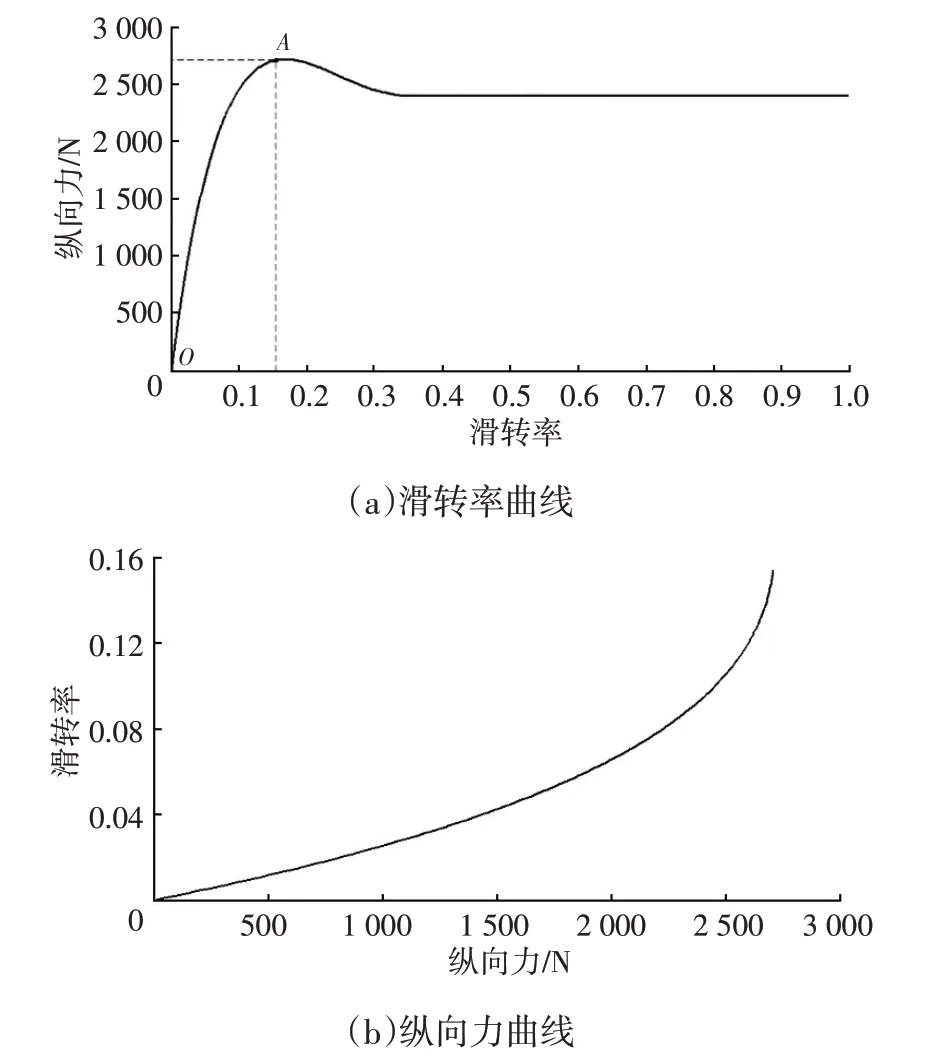
图4 滑转率与纵向力曲线

由于车辆正常驾驶中驱动轮不会产生剧烈滑转，其滑转率将维持在图4a 中的OA段内，即Fx同滑转率s保持单调关系，故可由纵向力Fx估计车辆当前的滑转率，即s=f-1(Fx)，其图像见图4，采用多项式进行拟合：

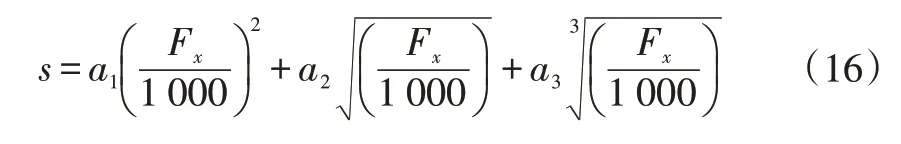
式中，a1、a2、a3为待定系数，通过插值拟合得到。

图5 模型结果与拟合结果对比

4.2 轮胎模型动态参数求解

试验车辆行驶过程中，仅前轮产生驱动力矩，后轮视为自由滚动，仅对前轮轮胎刷子模型待定参数进行求解，其中待定系数λ可联立式（7）和式（14）获得：

随后求出d，并代入式（15）即可求解Fx。

为检验刷子模型在TPMS上的简洁性和有效性，采用CarSim整车模型，接入Simulink搭建的刷子模型进行联合仿真，同时CarSim 接入自身使用的魔术公式进行轮胎力分析，其仿真模型结构如图6所示，Fx1～Fx4分别为左前、右前、左后、右后轮纵向力。

仿真车辆在平直公路上从静止起步匀加速驾驶，加速度为1 m/s2，仿真结果对比分析如图7所示。

图6 仿真模型结构

图7 仿真输出结果

由图7 可知，除换挡时刻，整个过程驱动轮所受纵向力基本一致，说明在正常直行工况下，参数更为简单的刷子模型在不考虑纵、侧向联合工况的情况下，用于纵向力分析效果较为理想。

5 胎压监测系统参数的估计

5.1 所需工况的限定条件

车辆的实际行驶状态由驾驶员和道路条件决定，具有一定的随机性，因此要对实际的轮速传感器信号进行重构，使其稳定且便于TPMS使用。CAN信号筛选过程如图8所示。基于车辆CAN总线的报文发送周期T，对每一发送周期内的报文进行筛选。

图8 CAN信号筛选示意

5.1.1 轮速信号的分离

通过车辆加速度ac和车速对信号Vi进行约束，依据不同的条件分离轮速信号：

式中，as为车辆实际行驶中可视为匀速运动的加速度允许波动值；Vs、Vf分别为允许录入的最小和最大车速。

对CAN 发送周期内的数据先利用式（18）进行判断，提取符合条件的数据，过滤不符合条件的数据。以一段实际驾驶数据为例，分离结果如图9 所示，其中as=0.2 m/s2。

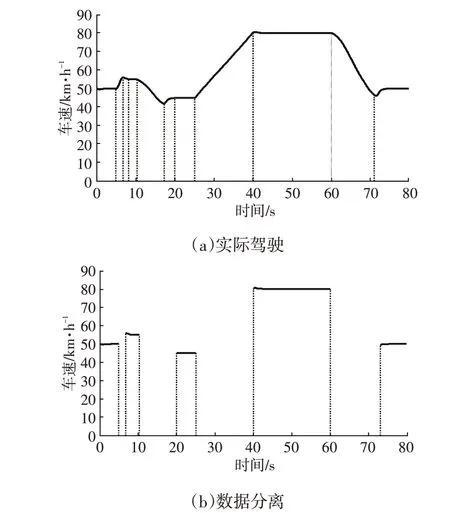
图9 数据分离示意

5.1.2 轮速信号的重构

车辆CAN 总线上的轮速信号结构为每个周期T内各车轮轮速传感器检测到的脉冲数变化量，可记为n=[n1n2n3n4]；在每一个CAN 发送周期内，满足式（18）的数据依据车速依次进行分类统计，分离后信号再处理结果如图10 所示。

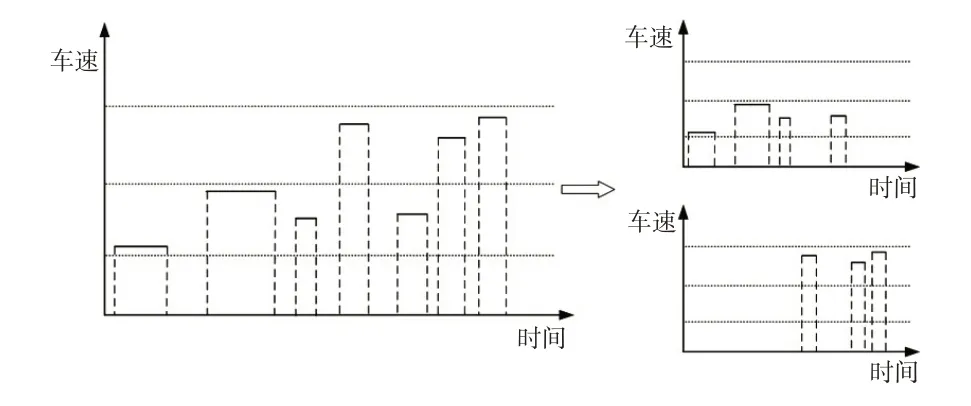
图10 分离后信号再处理

对同一种车速范围内的信号进行信息重构，其操作为：

式中，Ni为满足式（18）的Vi的4个车轮脉冲累计和。

5.2 参数预估

5.2.1 轮速信号截止条件

设N=[N1N2N3N4]T，轮速信号截止条件为N中的任一Ni满足：

式中，Nmax为常数，依据车辆结构决定[17]，根据经验，常设置为车辆行驶200 m中轮速传感器所采集到的脉冲数。

5.2.2 基于车速求解驱动轮滑转率

对于达到截止条件的Ni，其对应的车速为Vi，联立式（4）、式（16），可得：

5.2.3 基于滑转率求解TPMS参数

由式（9）的滑转率定义，在车辆实际行驶中，从动轮接近自由滚动，且间接式TPMS 求解的是相对关系，将其作为车速参考，滑转率公式变形为：

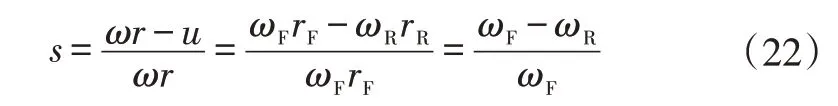
式中，ωF、ωR分别为驱动轮、从动轮角速度；rF、rR分别为驱动轮、从动轮半径。

其中，以左前轮为例，在实际应用中，车轮角速度为ω1=2πn1/n0T，其中n0为车轮旋转一周的脉冲数，T为轮速计数周期[19]，因此得到轮速传感器信号同滑转率的关系为：

式中，nF、nR分别为驱动轮、从动轮在1个CAN周期内传感器所测得的信号脉冲数。

即当车速稳定时，nF、nR基本维持不变，进一步得到：

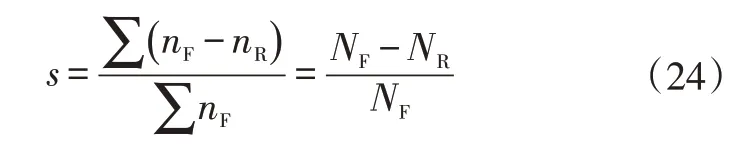
式中，NF、NR分别为到达轮速信号截止条件时，驱动轮、从动轮累计的脉冲数。

由此可得从动轮脉冲数的补偿量ΔNR为：

联立式（21）、式（25），最终得到：

在车辆行驶过程中，针对每一个监测周期内的车速，对从动轮进行轮速信号补偿，补偿后的轮速信号为：

补偿后的轮速信号数据用于TPMS，实现高速行驶过程中依据车速对采样轮速信号的动态补偿，弱化系统判断参数在高速行驶中的波动，提高TPMS在高速工况下的性能。

6 实车验证

试验车辆空气阻力系数CD=0.37，4个轮胎胎压为标准气压。在正常自由驾驶过程中，按照本文中轮速信号的分离与重构对轮速信号进行过滤，将筛选后的数据用于TPMS系统的运算。

试验中采集车辆几种匀速工况与驱动轮、从动轮间的轮速信号差异[20]，如表1所示，其截止条件为Nmax=5 000。

表1 试验车辆数据记录

仅将车速20～100 km/h 的数据用于式（26）中待定系数的求解，得到a1=0.493、a2=-42.58、a3=324.49。根据求解出的方程再对车速100 km/h以上进行预测，观察补偿方程能否能够达到良好的预测效果。补偿方程预测结果如图11所示。

图11 补偿方程预测结果

从图11中可以看到，实际的预测效果满足要求，但在低速段曲线不能完全符合实测数据，原因在于低速工况下，车辆行驶阻力中空气阻力并未占主要成分，仅根据车辆空气阻力方程无法有效计算车轮所受纵向力，故在TPMS实际应用中，在车辆达到一定车速前，不对车辆进行轮速信号补偿，就试验车辆而言，在车速达到90 km/h后开始进行轮速信号补偿。具体补偿方法为：

7 结束语

本文对车辆行驶过程进行了动力学分析，结果表明，TPMS 高速工况下性能降低的主要原因是随车速的增高，气动力开始对车辆受力产生明显影响，其中空气阻力直接导致驱动轮受力增大，造成驱动轮滑转率增大，系统参数开始出现分离。

结合实车测试结果，本文基于刷子模型，通过对轮胎纵向刚度、滑转率和驱动状态的分析建立了轮速信号补偿方程，并对提出的轮速信号补偿方法进行了验证，结果表明，该方法在高速工况下能够有效估计TPMS参数补偿量的变化。