车辆横向稳定性自适应预测控制＊

杨维妙 张建武 冯鹏鹏

（上海交通大学，上海 200240）

1 前言

车辆横向稳定性控制历来是研究人员关注的重点。传统的稳定性控制系统诸如防抱死制动系统（Antilock Brake System，ABS）、牵引力控制系统（Traction Control System，TCS）以及电子稳定性控制系统（Electronic Stability Program，ESP）等，都是基于车辆的机理模型进行设计的[1-3]。然而，由于车辆模型具有复杂性，这些系统在建模过程中会不可避免地进行简化，引起模型精度的降低，进而影响控制器的有效性。另一方面，在控制对象的建模中很难考虑轮胎力与车速等时变因素带来的影响，使得实际控制器对于非定常模型的适应性大幅降低。因此，如何设计一种考虑时变模型特性且精度较高的稳定性控制器成为车辆动力学领域中的研究难点。

相比于传统的车辆控制器设计方法，基于子空间模型辨识的控制器近些年来受到极大的关注[4-5]。该方法基于子空间理论，利用系统的输入、输出数据对系统模型进行辨识，结合线性二次高斯（Linear Quadratic Gaussian，LQG）准则[6]，可以实现一种基于数据驱动的无模型广义预测控制器。目前，该方法在车辆动力学领域应用的局限性在于：传统子空间辨识理论的适用对象为开环线性系统，对于“人-车-路”闭环的非线性系统，其辨识精度大幅降低[7]；在子空间预测控制器设计的经典子空间辨识方法中大量使用奇异值分解（Singular Value Decomposition，SVD）和RQ分解等数值计算工具，计算量巨大，不利于在线递推实现[8]。综合以上两点，本文基于子空间模型辨识理论，设计出一种适用于非线性闭环车辆动力学系统的自适应预测控制器，并结合7自由度整车动力学模型进行数值仿真验证。

2 整车动力学建模及验证

2.1 7自由度车辆动力学模型

整车动力学模型的目的是准确反映车辆的动力学特性，以便作为稳定性控制器的验证平台。针对车辆稳定性控制器研究，相对快速有效的数值建模方法，如Simulink 建模方法，目前在车辆动力学领域被广泛采用。考虑到建模复杂度，7自由度车辆动力学模型具有综合的性能优势，在考虑4 个车轮运动的同时，加入了车辆纵向、侧向以及横摆方向的运动，能够十分准确地反映车辆行驶过程中的横向动力学特性，该模型如图1所示。

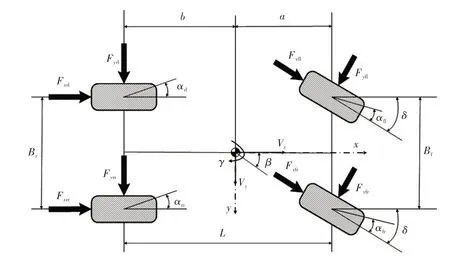
图1 整车动力学模型

基于汽车系统动力学相关知识，本文在MATLAB/Simulink环境中建立7自由度车辆模型：

式中，m为整车质量；Bf、Br分别为前、后轴的轮距；a、b分别为质心与前、后轴的距离；Iz为车辆的横摆转动惯量；J为车轮的转动惯量；Rd为轮胎滚动半径；δ为车辆前轮转角；Vx、Vy分别为车辆的纵向、侧向车速；γ为横摆角速度；ωij（i=f,r 分别代表前、后轴；j=l,r 分别代表左、右轮）为各车轮的转速；Tdfj为左、右前轮等效驱动力矩；Tbij为各车轮施加的制动力矩；Fxij、Fyij分别为各车轮上由PAC2002 轮胎模型计算得到的纵向力与侧向力。

2.2 道路试验

本文根据国际标准ISO 3888:1999 以及ISO/DIS 7401:2000，在襄樊汽车试验场利用某型前驱轿车分别进行了急剧双移线（Double Lane Change，DLC）和转向盘转角阶跃输入道路试验，试验及相关数据采集设备如图2所示。试验过程中分别采集了车辆的质心侧偏角、横摆角速度、转向盘输入转角、纵向车速、侧向车速以及侧向加速度等信息，采样周期为1 ms。

图2 整车道路试验及数据采集装置

2.3 车辆模型验证

以2.2 节中整车道路试验采集的转向盘转角和车速等数据作为模型的输入信息，选取车辆稳定性研究中常用的横摆角速度和车辆质心侧偏角作为输出信息，基于7 自由度Simulink 模型进行了数值仿真，并结合道路试验数据进行对比，结果如图3 所示。根据仿真结果可知，所建立的车辆动力学模型基本能够对行驶过程中的车辆动力学特性进行较为准确地描述。因此，可以作为后续稳定性控制器设计时的验证平台。

图3 2种工况下的仿真与试验结果对比

3 自适应预测控制器设计

3.1 子空间马尔可夫参数估计

设车辆控制对象的状态空间模型为：

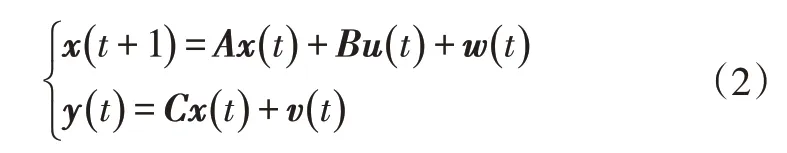
式中，xT(t)∈Rn、yT(t)∈Rl、uT(t)∈Rm分别为系统的状态、输出和输入向量；A∈Rn×n、B∈Rn×m、C∈Rl×n为系统模型矩阵；wT(t)∈Rn、vT(t)∈Rl为过程噪声与测量噪声。

基于卡尔曼滤波过程可将式（2）改为新息形式：

根据基于预测器的子空间辨识（Predictor Based Subspace Identification，PBSID）理论[9]，可将式（3）转化为预测器形式，即

利用参考时刻k，将系统的数据分成“过去”和“将来”2 个数据集：和，将上式中的状态方程不断迭代，可得：

式中，p为过去数据集的长度。

当p足够大时，若的特征值位于单位圆内（此条件为子空间辨识的后验条件，在辨识过程中通过计算系统矩阵的特征值对其进行验证），则，故：

式中，Γ∈Rlf×n为广义能观矩阵；H为托普利兹（Toeplitz）矩阵；Y、X、Zf、E为相应的系统向量构成的数据矩阵。

结合式（6），式（9）可转化为：

式中，M为马尔可夫（Markov）矩阵。

M的表达式为：

式中，mi为M的参数。

根据式（11），将式（9）左边的y(t)展开，即可得：

通过式（12）即可利用最小二乘法，结合系统的输入、输出数据y(t)、u(t)对mi进行估计，进而构造出M。

3.2 托普利兹矩阵H更新

对于能观与能控性系统，Γ∈Rlf×n至少包含n个互不相关的行向量，根据辨识车辆模型结构，可构造出置换矩阵S∈Rlf×lf，实现如下分解：

式中，P为传播因子矩阵[10]。

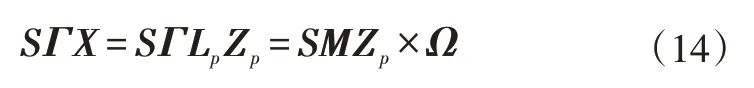
将式（13）带入到式（14）中，则：

因此，有Ω2=PΩ1。由于向量Ω可利用系统数据以及马尔可夫矩阵M计算求得，故可设计出一个二次准则方程，对P进行求解：

同样，利用最小二乘法即可求得式（16）中的传播因子矩阵P，最终获得广义能观矩阵Γ的递推更新值。系统矩阵C可直接根据Γ的结构求解计算：

同理，通过分析M的矩阵结构，可以获得系统矩阵A和B。进而根据式（11）构造出托普利兹矩阵H。

3.3 自适应预测控制器设计

根据上述递推计算求得的M和H，并结合式（6）将式（8）的第1列展开，并忽略误差项E，有：

式（18）即为基于子空间辨识的预测器形式。由预测器的结构形式可知，在求得其系统参数矩阵并已知系统未来输出的情况下，将递推的子空间预测过程转化为预测控制过程，即可设计出预测控制器，其逻辑关系如图4所示。

图4 子空间预测器与预测控制器

由于zT(t)=[uT(t)yT(t)]，因此式（18）中，

式中，†为Penrose-Moore逆。

若已知系统的未来参考输出r以及过去的输入、输出数据ϕ，则可利用LQG 准则计算系统的预测控制率uf：

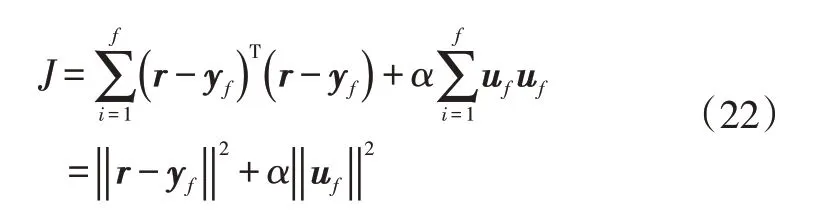
式中，α为遗忘因子。

最小化上述方程，则可求得车辆自适应预测控制律：

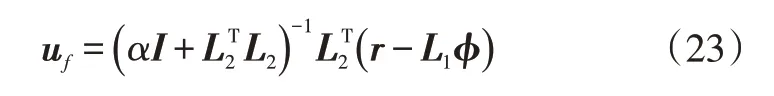
至此，即可利用递推子空间模型辨识算法，针对车辆的横向稳定性，提出具有模型自适应特性的预测控制器，其算法流程如图5所示。

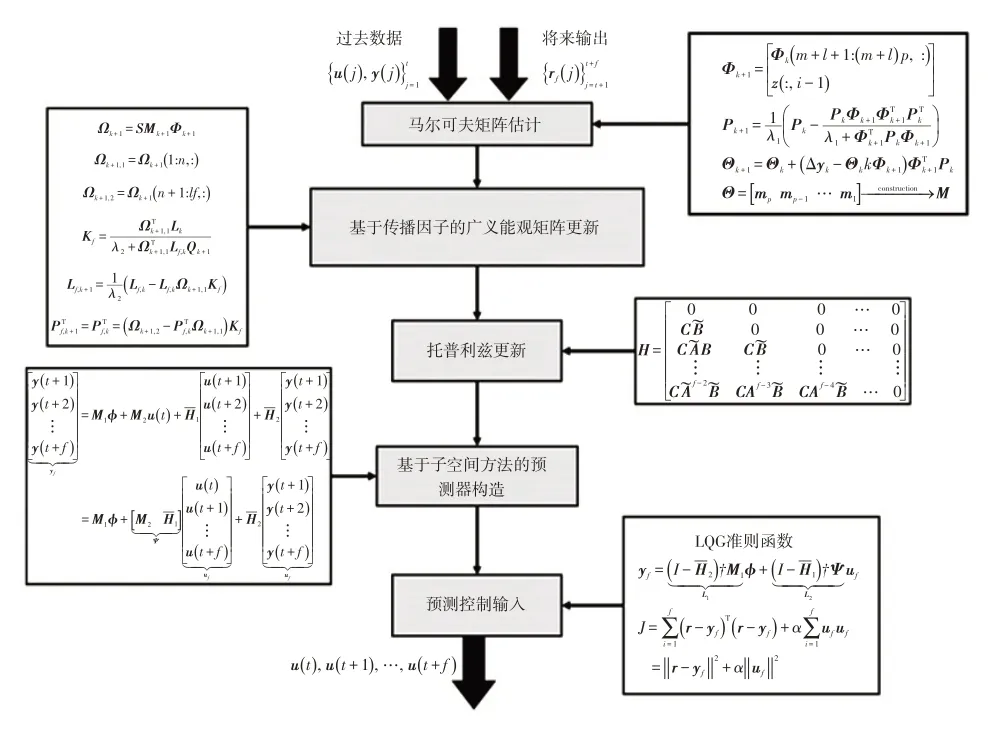
图5 基于子空间辨识的自适应预测控制器算法流程

4 数值仿真验证

根据前文推导出的自适应预测控制算法，针对车辆的横向稳定性，可建立如图6 所示的控制器架构，其中系统输出量为横摆角速度与质心侧偏角，控制量为车辆的前轮转角。其控制原理为：根据车辆的参考输入以及系统当前时刻和“过去”p段时间窗的输入、输出数据，利用递推子空间辨识算法对预测控制器的模型矩阵进行实时辨识与构造，利用辨识出的控制器模型计算出最优的前轮转角输入，从而对车辆的横向稳定性进行控制。其中，参考横摆角速度通过经典的2自由度线性车辆模型计算获得。文献[11]指出，应当在行驶过程中使质心侧偏角尽量保持较小的值，进而保证车辆的安全性。因此，参考质心侧偏角在数值仿真过程中取值为0。

根据上述控制架构，基于7自由度整车模型，利用道路试验数据分别进行了双移线和转向盘转角阶跃输入工况的数值仿真验证。仿真过程中的车速为100 km/h，路面附着系数为0.8，均与道路试验保持一致。图7 给出了两种工况下子空间算法辨识出的系统矩阵特征值。从仿真结果可以看出，在辨识过程中，系统矩阵的特征值始终位于单位圆内，对子空间算法的充分条件进行了后验，保证了辨识过程的可行性。

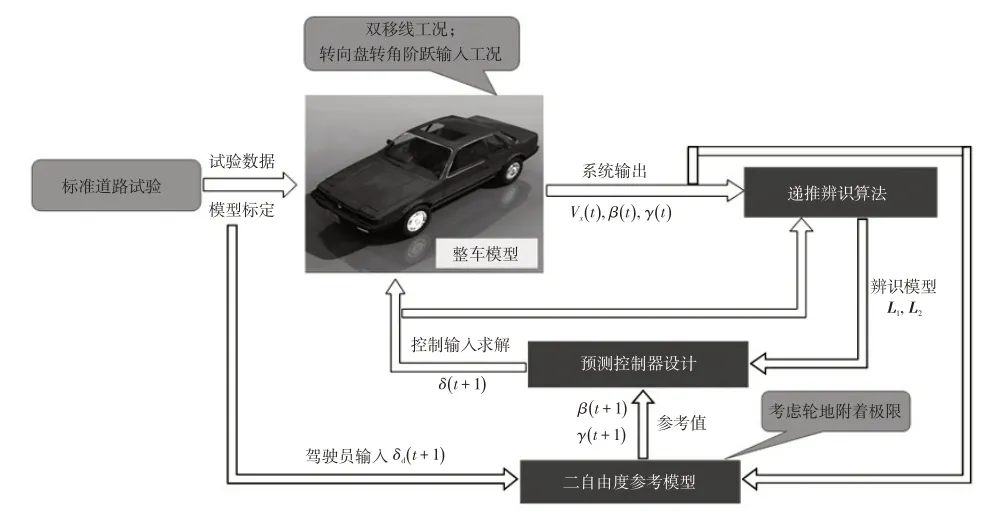
图6 车辆横向稳定性控制架构

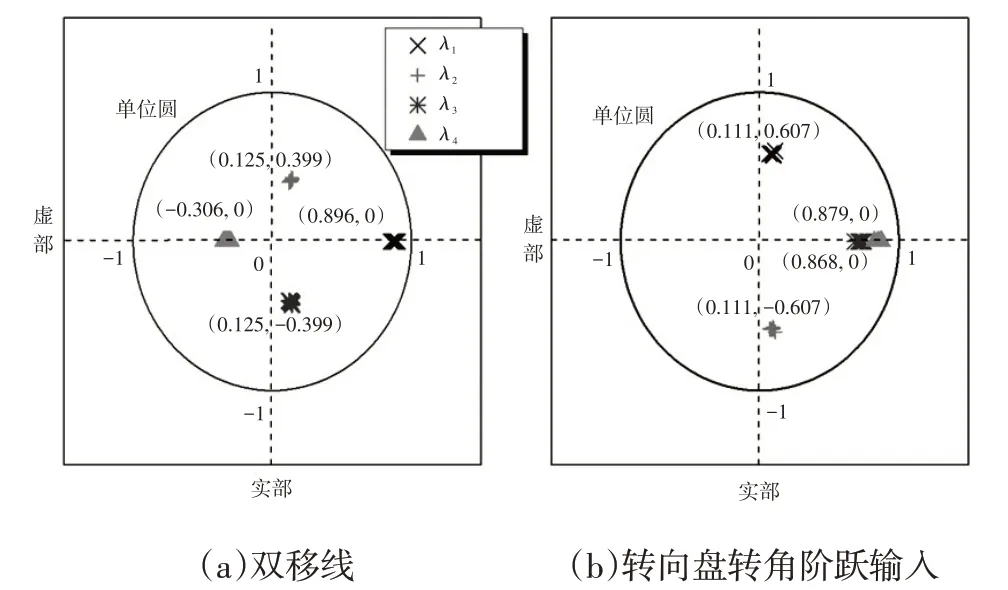
图7 2种工况下仿真过程中的辨识系统矩阵的特征值

根据仿真结果，利用β-γ相平面法[12]对车辆动力学仿真过程中的稳定性进行了分析，结果如图8 所示，其中阴影部分为由文献[12]方法确定的稳定性区域。显然，当车辆处于开环无控制状态时，车辆的横向动力学特性处于非稳定性区域，而本文设计的自适应预测控制则可以使车辆始终保持在稳定区域。

图9a、图9b、图10a和图10b分别给出了2种工况下车辆自适应预测控制器的控制效果。车辆在高速行驶过程中，若仅依靠驾驶员控制转向盘（即处于开环无控制状态），横摆角速度会出现很大的超调量，同时，质心侧偏角的幅值也相对较大，不利于车辆的稳定性和安全性。相比于开环过程，本文提出的自适应预测控制器能够保证横摆角速度准确地跟踪参考模型，同时减小质心侧偏角的幅值，大幅提高了车辆的横向稳定性。

此外，图9c、图9d、图10c 以及图10d 分别给出了2种工况下的车辆前轮转角与轮胎侧偏角。由仿真结果可以看出，相比于无控制过程，预测控制器能够降低车辆稳定所需的转向盘转角，并能减小前轮的侧偏角，保证了车辆稳定性的同时能够减小轮胎对于侧向力的利用率，根据轮胎的“摩擦圆”特性可知，此举能够降低主动转向过程对于制动力的影响，保证车辆行驶过程中具有足够的制动性能。

图8 2种仿真工况下的车辆稳定性相平面

图9 双移线工况仿真结果

图10 转向盘转角阶跃输入工况仿真结果

5 结束语

本文基于子空间理论和传播因子方法，提出了一种基于递推子空间模型辨识的自适应预测控制算法，并对算法的实现过程进行了详细推导。根据算法特征可知，基于子空间的自适应预测控制器具有纯数据驱动、无需模型的先验知识等性能优势，并且具有一定的模型自适应特性。

针对车辆的横向稳定性，本文设计了基于自适应预测控制器的架构，并进行了整车动力学数值仿真。利用仿真过程中辨识模型的系统特征值，对子空间算法的可行性进行了后验。根据双移线工况和转向盘转角阶跃输入工况下的仿真结果可知，结合前轮主动转向的自适应预测控制器能够有效保证车辆行驶的稳定性，并降低对于车辆前轮制动性能的影响。