基于硬件在环与远程参数控制技术的半主动悬架车辆道路模拟试验

孙野 于长清 巫洋

（1.中国第一汽车股份有限公司研发总院，长春 130013；2.汽车振动噪声与安全控制综合技术国家重点实验室，长春 130013）

1 前言

车辆耐久性能是决定整车质量的重要一环，整车道路模拟试验在车辆耐久性考核中起着重要作用，可以在室内实现车辆在试验场典型工况下行驶时的振动状态，并能快速有效地对车身系统、悬架系统及主要零部件进行耐久性评价，在整车设计开发过程中及早暴露车辆设计缺陷及结构缺陷，为车辆结构设计优化提供改进依据[1-5]。

目前，道路模拟试验主要针对传统螺旋弹簧减振器车辆进行[6-9]。随着技术的进步，很多高端车辆配备半主动悬架，其通过悬架电子控制单元（Electronic Control Unit，ECU）对车辆行驶过程中的CAN 报文进行分析计算[10-11]，根据不同行驶工况控制悬架的特性状态。半主动悬架的减振器阻尼特性介于硬阻尼特性曲线和软阻尼特性曲线之间，且在车辆行驶过程中实时变化，因此，对半主动悬架车辆进行道路模拟试验时需要实时控制减振器阻尼特性。

据了解，国内尚没有针对半主动悬架车辆进行道路模拟试验的研究，部分研究人员采用将主动减振器变阻尼特性更改为固定阻尼特性的方法进行试验，但车辆行驶状态与实际不一致，导致试验结果失真，国外仅有少数车企曾进行过相关试验方法的开发。

本文基于半主动悬架车辆的悬架控制策略，提出通过硬件在环（Hardware-In-the-Loop，HIL）与远程参数控制（Remote Parameter Control，RPC）技术联合仿真的方法进行道路模拟试验，可在试验过程中实时同步控制半主动悬架状态，复现车辆在典型工况下行驶时的运动姿态，实现半主动悬架车辆的道路模拟耐久性考核。

2 联合仿真原理

本文搭建的联合仿真系统原理如图1所示。其中，为保证悬架运动状态与载荷谱信号实时同步，将CAN报文信号分为CAN 报文动态信号和CAN 报文静态信号，HIL仿真系统将RPC系统发送的CAN报文动态信号与仿真的CAN报文静态信号实时整合后发送给电控悬架ECU，电控悬架ECU控制车辆悬架特性，使整车振动状态与车辆在试验场行驶时的振动状态一致，实现对半主动悬架车辆的道路模拟试验。

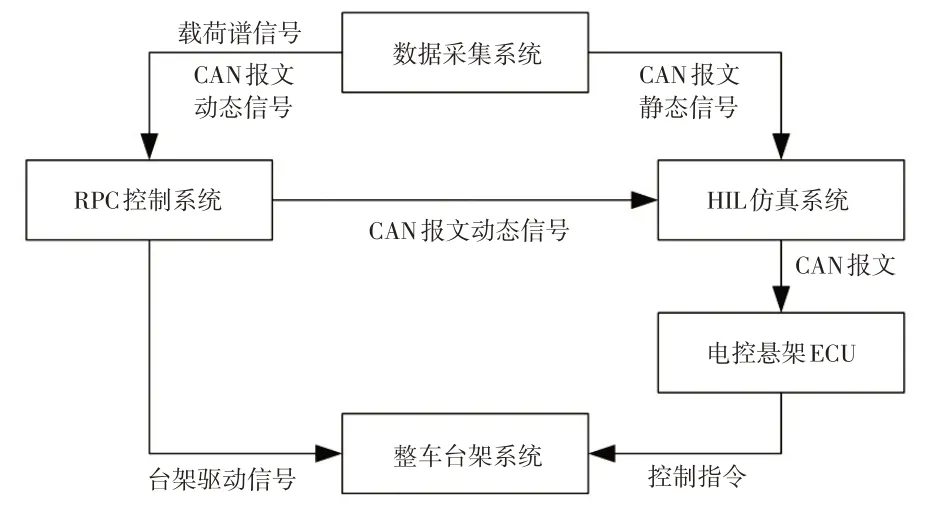
图1 HIL与RPC联合仿真原理

将整车台架系统假定为线性时不变系统[12-13]，通过RPC系统生成的粉红噪声驱动信号驱动系统运行，由输入信号与输出信号的关系可求出频响函数矩阵，通过已知的期望响应信号即可反求出所需要的驱动信号。由于实际整车台架试验中存在很多非线性因素，导致使用线性系统假定求得的驱动信号驱动系统运行时，所得响应信号与期望响应信号存在误差，需通过迭代修正驱动信号，消除系统非线性的影响，最终求出满足试验要求的驱动信号。

3 数据采集

3.1 载荷谱数据采集

为快速有效地模拟车辆在典型工况下的振动状态，以及迭代后对迭代效果进行数据分析，采集的载荷谱信号一般包括迭代控制信号和监测信号。

控制信号作为道路模拟试验中的迭代目标信号，信号测点的选取直接影响迭代效果，其选取原则为：测点信号响应需尽可能与某一驱动通道相关性高，而与其他驱动通道相关性低，从而便于迭代快速收敛。本文选取的控制信号包括轮心六分力信号、轮心加速度信号、减振器位移信号，以及相关悬架零部件应变信号。

监测信号用于对车辆相关监测点迭代效果进行分析，测点主要选取试验车辆危险点、运动姿态关注点等。为保证模拟的半主动悬架车辆振动状态与典型工况下行驶时振动状态一致，本文选取减振器上支座位置加速度作为监测信号，用于监测和分析车身运动姿态。

具体载荷谱数据采集信号及传感器情况如表1所示。

表1 采集信号及传感器

3.2 CAN报文信号采集

采集车辆CAN 总线报文信号，用于在道路模拟试验中发送给悬架ECU，控制减振器阻尼状态。采集的信号需保证与载荷谱信号时间同步，本文试验采集的CAN报文信号包括驾驶模式系统（Driving Mode System，DMS）、电动助力转向系统（Electric Power Steering，EPS）、车身电子稳定系统（Electronic Stability Program，ESP）和网关（Gateway）等网络节点信息。

3.3 采样频率

车辆在典型工况下行驶时，造成损伤的主要是50 Hz及以下频率成分，故道路模拟耐久试验中模拟的最高频率为50 Hz。依据奈奎斯特采样定理[13]，为保证数据准确性，以及不出现信号混叠，实际数据采样频率fs需满足：

式中，fN为采集信号的最高频率。

为尽可能多地保留道路载荷谱成分，本文选定采样频率为512 Hz，该频率亦能够满足CAN 报文信号采集要求。

4 频响函数求解

4.1 系统模型

道路模拟试验台架与车辆组成的系统可简化为多输入、多输出系统，如图2 所示，其中，X(ω)、Y(ω)分别为系统输入、输出信号矩阵，Γ(ω)、Ψ(ω)分别为输入端、输出端噪声干扰信号，噪声干扰信号与输入、输出信号不相干，H(ω)为系统频响函数矩阵。

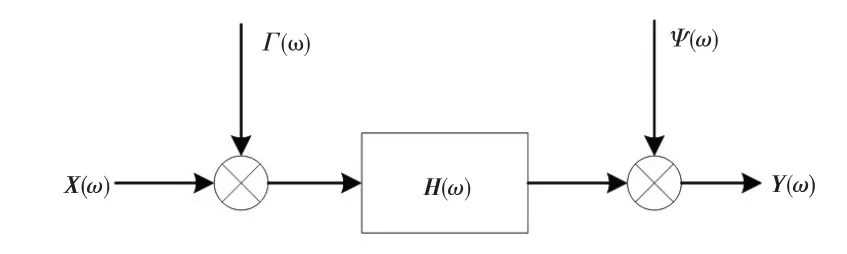
图2 输入、输出系统模型

4.2 频响函数估计方法

使用粉红随机噪声驱动信号驱动整车台架系统运行，输出系统响应信号，通过频响函数估计可求得系统频响函数。

常用频响函数估计方法为H1估计法和H2估计法[14]。H1估计法假设只存在输出端噪声干扰信号，且与输入、输出信号不相干，未考虑输入端噪声干扰信号的影响，得到的频响函数估计值比真实值小，为欠估计状态；H2估计法假设只存在输入端噪声干扰信号，且与输入、输出信号不相干，未考虑输出端噪声干扰信号的影响，得到的频响函数估计值比真实值大，为过估计状态。H1估计法和H2估计法的估计值都是有偏的，而在道路模拟试验中，相比输入端，输出端会混杂更多的噪声干扰信号，H1的估计值更接近真实的H(ω)，故本文选取H1估计法计算频响函数。

H1估计法频响函数估计结果为：

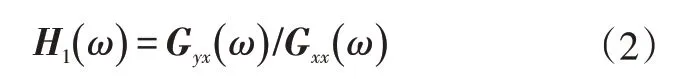
式中，Gyx(ω)为输出与输入信号互功率谱密度；Gxx(ω)为输入信号自功率谱密度。

H1(ω)与实际系统频响函数H(ω)的关系为：

式中，Gγγ(ω)为输入端噪声干扰信号自功率谱密度；Guu(ω)为实际输入信号自功率谱密度。

4.3 频响函数

本文通过频带宽度为0.1～50 Hz的粉红随机噪声信号驱动系统运行，应用H1估计法计算得到半主动悬架车辆与台架系统频响函数，左前轮纵向、侧向、垂向驱动通道与前轮轮心纵向、侧向、垂向载荷Fx、Fy、Fz响应通道频响函数矩阵图如图3所示。

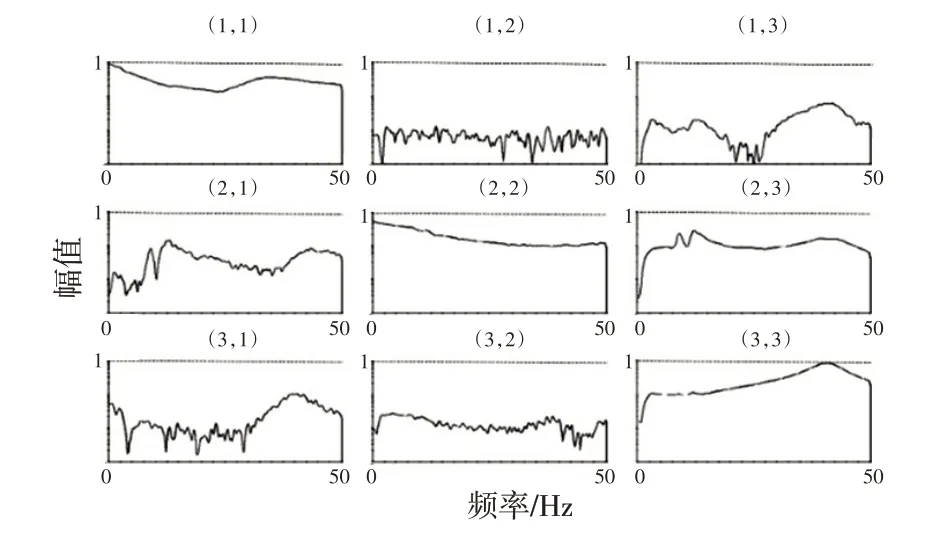
图3 频响函数矩阵

频响函数反映了系统的信号传递特性，各测点响应耦合了来自所有驱动通道激励的叠加。其中，传感器受所在位置对应驱动通道的影响更大，在频响函数矩阵图中应主要关注响应通道与其对应的驱动通道的相关性。由图3 可知，主对角线频响函数在50 Hz 范围内波动小，相关性较好，其他频响函数波动较大，原因是其测点对该驱动的响应较弱，响应与驱动相关性差。(1,1)、(2,2)频响函数随着频率增加有所下降，原因是随着频率增加，信噪比减小，频响函数受噪声干扰增大；(3,3)频响函数随着频率增加有所升高，在42 Hz 左右出现峰值，原因是该响应通道谐振频率附近的激励使系统产生共振。相关通道对驱动的响应越强，不相关通道对驱动的响应越弱，则越有利于系统控制。还可通过增加粉红随机噪声激励时间提高频响函数辨识精度。

5 迭代

相比传统车辆，半主动悬架车辆系统特性不确定，迭代更加难以收敛，本文采用非方阵迭代方法，增加响应控制通道，使更多响应通道参与迭代，以便更好地控制车辆的运动状态。但响应通道越多，通道之间会产生更多干扰，就越不利于迭代收敛，这就需要依据经验和车辆受力情况选取合适的响应通道参与迭代，其中，减振器位移直接反映减振器运动特性，故该通道在半主动悬架车辆道路模拟试验中需参与迭代。

5.1 迭代算法

频响函数表征了试验系统的特性，其与输入信号和输出信号的关系式为：

通过傅里叶变换计算频域期望响应Yd(ω)为：

式中，Yd(t)为时域期望响应信号。

计算频域初始驱动信号X0(ω)为：

式中，α为衰减系数。

通过傅里叶逆变换计算初始驱动信号X0(t)为：

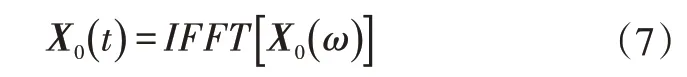
用初始驱动信号X0(t)驱动试验系统运行，得到第1 次响应信号Y1(t)，依次进行迭代，第i次响应信号为Yi(t)，则响应信号与期望响应信号的时域误差ΔYi(t)为：

频域响应误差ΔYi(ω)为：

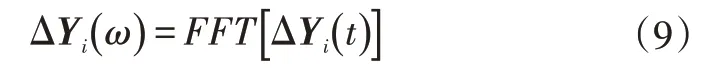
第i次频域驱动信号修正ΔXi(ω)为：

计算驱动修正信号ΔXi(t)为：

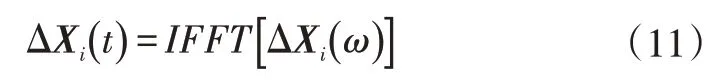
修正后的驱动信号Xi(t)为：

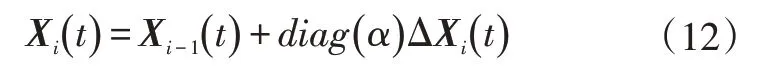
依次进行迭代，当响应信号误差满足试验要求时，迭代结束，得到的驱动信号作为试验的最终驱动信号。

5.2 迭代误差

迭代过程中，收敛情况应用台架响应信号相对期望响应信号的均方根误差进行评价，分析响应信号的迭代偏差，均方根误差Err计算方法为：

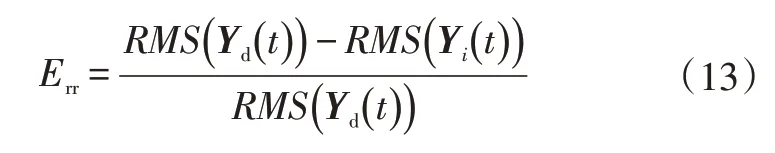
在半主动悬架整车道路模拟试验中，一般要求六分力通道均方根误差小于20%，其他参与迭代的控制通道，如加速度、位移、应变等，均方根误差小于30%。误差越小说明迭代效果越好，道路模拟试验越准确。

本文以重庆某汽车试验场路障路为例，前轮轮心载荷Fx、Fy和Fz迭代均方根误差如图4所示。由图4可知，经过24次迭代，轮心载荷均方根误差可达到10%左右，试验误差较小，轮心受力与道路试验基本一致。

图4 轮心载荷均方根误差

减振器位移迭代误差在试验中能够直接反映出台架试验与实际路试中减振器特性状态是否一致，所以，在半主动悬架车辆道路模拟试验中，由减振器位移信号收敛情况可知减振器是否处于正确的特性状态，本文选取的部分典型工况减振器位移迭代误差如表2所示。

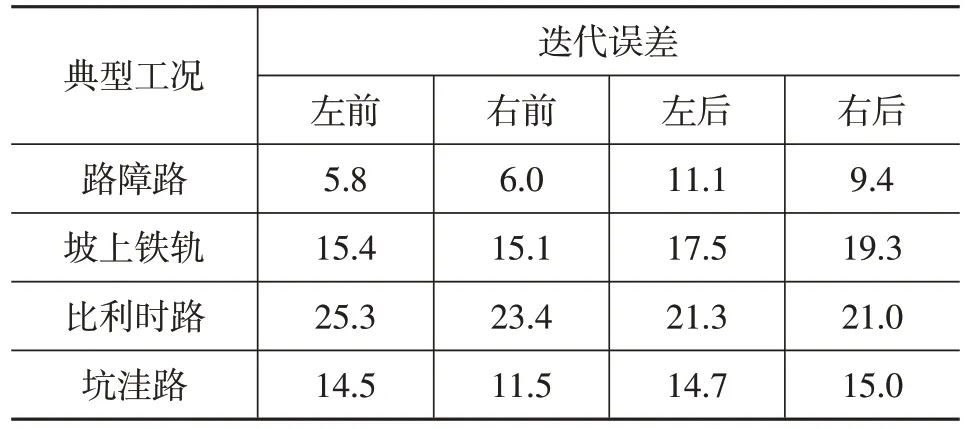
表2 减振器位移迭代误差 %

由表2可知，各典型工况中减振器位移迭代误差均位于30%以下，符合迭代误差要求，说明减振器处于正确特性状态。若减振器处于非正确特性状态，则减振器位移不收敛，误差较大，时域上表现为幅值偏大或偏小、相位存在偏差等情况。

5.3 伪损伤分析

道路模拟试验是对车辆耐久性的考核，将车辆在道路模拟试验中受到的损伤与车辆在实际试验场中受到的损伤进行对比，分析车辆各控制通道与监测通道的损伤误差，若对比结果满足误差范围要求，则认为道路模拟试验与实际试验场试验等效。

根据S-N曲线定义，在恒定应力σ作用下，当载荷循环次数达到N时，零件完全损伤或失效[15]。依据帕姆格伦-迈因纳（Palmgren-Miner）线性疲劳损伤累计理论，每一个载荷循环都会为零件的损伤作出“贡献”，当零件在恒定应力σ作用下的载荷循环次数n小于失效循环次数N时，产生的损伤d为：

在不同应力水平σi作用下的总损伤D为：

式中，ni、Ni分别为应力载荷σi作用下的循环数和失效循环数；j为零件所受应力等级的数量。

由于很难获取车辆各零部件真实材料的S-N曲线，无法得知真实损伤数值，所以只能通过伪损伤对各测点进行比较，本文取反斜率为5 的材料S-N曲线进行计算，通过雨流计数法求得各应力载荷σi下的循环数ni，计算各测试通道的伪损伤，对计算结果进行评价，台架响应信号与期望响应信号伪损伤比值要求为：控制通道伪损伤比值在[0.5,2]范围内；监测通道伪损伤比值在[0.25,4]范围内。

本文按照试验场规范要求的典型工况循环数进行配比，计算得到各测点在道路模拟试验中和实际试验场中的伪损伤及伪损伤比值，选取部分通道对伪损伤比值进行说明，取右前轮轮心Fx、Fy、Fz，轮心X向加速度ax、Z向加速度az、减振器位移Dd等控制通道，和监测通道右前减振器上支座Z向加速度abz，所取测试通道伪损伤及伪损伤比值如表3所示。

表3 伪损伤及伪损伤比值

由表3可知，以上各测试通道伪损伤比值均在[0.5,2]区间内。轮心各通道、减振器位移通道、减振器上支座加速度通道损伤比值满足要求，说明车轮在台架激励时受力与路试受力损伤相近，主动减振器特性在台架试验中的状态与路试时基本一致，车身姿态控制较好，且减振器在车辆系统中对激励信号的传递与路试时一致。从各通道伪损伤比较可以看出，半主动悬架车辆道路模拟试验成功地对主动减振器进行了有效控制，半主动悬架处于正确运动特性状态，激励信号满足耐久性试验要求。

6 耐久性试验

依据试验场耐久性试验行驶规范，编制半主动悬架车辆道路模拟试验各工况驱动信号循环数及循环顺序，耐久试验中，半主动悬架减振器状态控制方式与迭代过程一致，同时，RPC 控制系统控制道路模拟试验台架运行，驱动半主动悬架车辆进行耐久试验，实现了对整车的耐久性考核。

7 结束语

本文针对半主动悬架车辆难以进行道路模拟试验的问题，提出了基于HIL仿真与RPC技术的道路模拟试验方法，实现了对半主动悬架车辆的迭代。结果表明，迭代响应信号伪损伤误差在合理范围内，在室内道路模拟试验台架上准确地复现了半主动悬架车辆在试验场典型工况的振动状态，并成功进行耐久试验。