基于自抗扰的永磁同步电机谐波抑制策略＊

王淑旺 夏麒翔

（合肥工业大学，合肥 230009）

1 前言

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）在新能源汽车领域被广泛使用，具有效率高、转矩密度大、调速范围宽等优势[1]。PMSM在工作过程中受死区效应、电气元件误差及导通压降、电机结构不对称等因素影响，会产生高次谐波，使三相电流发生畸变[2]，进而影响输出扭矩的稳定性和准确性[3]。针对这类问题，国内外学者展开了大量研究。文献[4]基于Maxwell 和Simplorer 软件建立联合仿真模型，用数值分析方法计算出3次谐波并注入电机控制环，成功减少了3、5、11、19次谐波分量，但会增加其他高次谐波。文献[5]提出了一种并联前馈用以补偿逆变器死区效应带来的5、7次谐波的方法，但对于其他原因形成的高次谐波没有作用。文献[6]、文献[7]基于PMSM矢量控制系统搭建数学模型，引入谐波电流环。文献[8]、文献[9]基于PMSM 电压模型，在电流环上并联谐振控制器，减少了5、7 次谐波分量，但会使不同频率的谐波互相影响，加大其他高次谐波含量。文献[10]以测试信号与测试速度为依据设计谐波抑制算法，实现了最佳谐波电流设计。文献[11]应用遗传算法计算并优化谐波电流的相位角及幅值，以减小转矩脉动。

针对三相电流畸变所引起的转矩脉动问题，本文提出一种基于自抗扰控制器（Active Disturbance Rejec⁃tion Control，ADRC）的谐波抑制算法，取代传统比例积分环节（Proportional Integral，PI）在电机电流环中的作用，并针对5、7 次谐波建立合适的数学模型，将交变谐波转换为直流量注入电机控制系统，以期提高电驱系统的稳定性。

2 谐波抑制数学模型

2.1 旋转坐标系变换原理

永磁同步电机控制系统是一个复杂、耦合的系统，存在大量交变变量。工程试验发现，5次负向、7次正向谐波在电机电流中占有较大比例，影响车辆的稳定性与NVH性能。对于交变变量，控制器不易控制，故可以使用Park、Clark 变换转化为直流量。这种方法极大地简化了PMSM的数学模型。运用这种思想，也可以进一步提取出电机电流中的5次负向谐波和7次正向谐波。电机电流坐标系如图1所示。

图1 旋转坐标系及静态坐标系

根据图1，结合Park 变换思路，可以推导出在旋转坐标系下，不同阶次坐标系之间相互转换的坐标变换矩阵为：

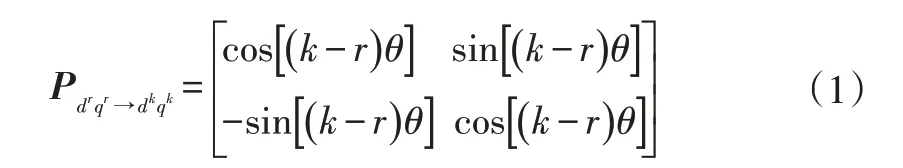
式中，r为原阶次；k为目标阶次；θ为转子位置。

2.2 补偿电压计算方法

式中，ud、uq分别为d、q轴电压；R1为定子电阻；id、iq分别为d、q轴电流；p 为微分算子；ω为电角速度；φd、φq分别为d、q轴磁链。

为了计算出5 次负向电流谐波，将r=-5、k=1 带入式（1），可得：

将式（3）两侧同时对时间t求导，且已知为常数，故可知其对时间求导结果为零，并再次将式（1）带入可得：

将式（4）带入式（2），进一步计算可得：

同理可得：

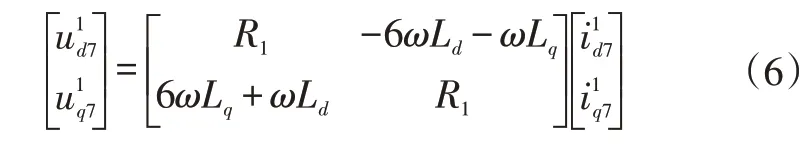
式中，Ld、Lq分别为d、q轴电感。

考虑到凸极永磁同步电机谐波之间的耦合性，将式（5）、式（6）相加，结合式（1）坐标变换矩阵进行计算，并提取出易于控制器控制的直流量，可得：

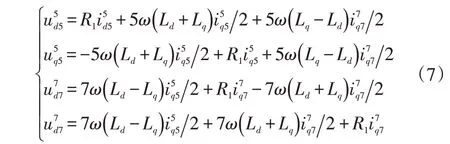
得到5、7次电压谐波后，转换到1次坐标系下，再相加即可得到应注入系统的总电压谐波。

3 自抗扰控制器模型

3.1 自抗扰控制器原理分析

传统PI 控制器最大的优势是简单且性能相对较好，其机理是基于误差进行反馈调节。本文所提出的谐波抑制算法本质上也是针对系统内、外扰动所造成的稳态误差进行补偿[12]。使用PI 控制器搭配谐波抑制算法时的不足主要有：系统无法对体现为非周期性的瞬时扰动作出及时且恰当的反应以消除其影响；被控量存在实际误差后再进行修正的方式必然存在时间上的滞后性。而自抗扰控制器可以从被控对象输出量中提取出扰动量，并在控制率中进行消除。排除电机内部扰动后，再对系统其他环节扰动所造成的高次电流谐波进行补偿，相较PI控制器性能更优。

自抗扰控制器包含跟踪微分器（Tracking Differenti⁃ator，TD）、非线性状态误差反馈控制率（Nonlinear States Error Feedback Control Laws，NLSEF）和扩张状态观测器（Expansion State Observer，ESO）[13]。其中，TD 可以跟踪输入信号及其微分信号减缓超调现象，ESO的作用是对被控对象的状态变量及其扰动信号进行观测，NLSEF对TD输出的控制信号及其微分与ESO观测到的系统输出进行处理与扰动补偿[14]。

3.2 自抗扰控制器设计

电机输出端的负载扭矩存在扰动，受控电机系统内部也存在着扰动，若电机电流环不能及时进行恰当处理，则系统容易出现偏差甚至失控，从而影响电机性能。

TD 相较于传统微分器有着跟踪速度更快、精度更高的优势，其微分信号与跟踪信号相对独立，使TD对于输入信号形式要求不高，有较大范围的通用性。TD 的阶跃响应为：

式中，x0为系统的输入；x1为输入跟踪值；x2为输入近似微分值；r为速度因子；h为滤波因子；f(x1-x0,x2,r,h)函数的具体表达式为：

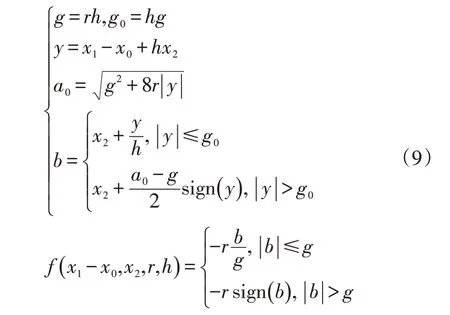
式中，g、g0、y、a0、b均为中间变量。

增大r会使TD的过渡时间减小，过渡时间过小时，TD 模块失去缓冲作用，过渡时间过大会影响系统响应速度，本文设r=30，h=0.001。

考虑到电流环状态表达式为一阶，故将TD 计算出的近似微分信号乘以步长，与跟踪输入信号相加作为输出，如图2 所示。TD 模块可以完成对输入信号的跟踪和滤波功能。

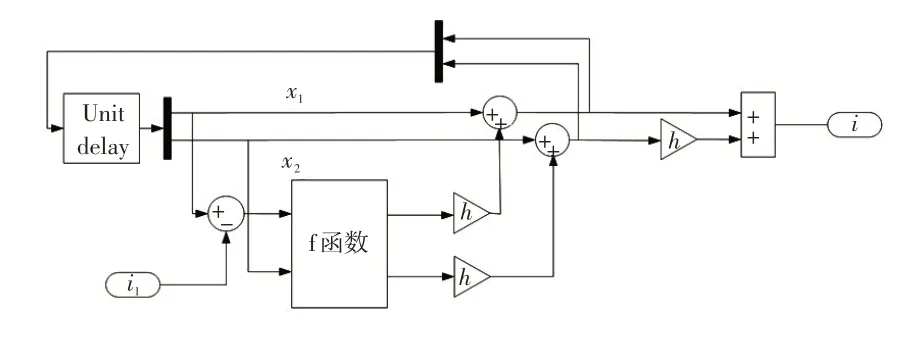
图2 跟踪微分器模型

由式（2）可得PMSM的状态方程为：

由式（10）可知，电角速度ω，以及d、q轴的电流、电压和电感波动均可视为系统的扰动来源。ESO 的原理是对受控系统的输入、输出量进行观测，这种方式决定了其并不依赖受控系统本身数学模型的特性。根据电流环状态方程，本文采取一阶ADRC 算法，电流环ESO计算公式为：

NLSEF 可以理解为优化后的PI 控制器，它采取非线性函数fal对系统误差进行处理，可以有效消除稳态误差及高频颤振。其计算公式为：

式中，if为电机测量电流；z1为电流观测值；为z1对时间的导数；z2为总扰动观测值；为z2对时间的导数；i为输入信号；e1、e2为状态变量误差；β1、β2、β3为增益参数，ESO特征多项式为(s2+β1s+β2)，习惯上将其设置为(s+c)2，本文取常数c=800，β3的取值参考PI取值方法；α1、α2、α3为非线性因子，一般在0～1 范围内取值，本文均取0.5；δ为滤波系数，本文取δ=0.001；b0为扰动增益系数，本文取b0=10；u0为NLSEF模块输出；u为电机系统输入。

fal(e,α,δ)具体表达式为：

式中，e为误差；α为非线性因子。

根据上述公式搭建仿真系统模型，ADRC 模型如图3所示，仿真系统模型如图4所示。

图3 ADRC仿真模型

3.3 自抗扰控制器稳定性证明概要

自抗扰控制器在工程实践中应用广泛，其理论稳定性证明有着重要意义和迫切需求。该证明方法已有学者进行研究，此处对证明思路总结概要，具体证明方法可参考文献[15]。

首先对ADRC 进行简化，令输入为0，则TD 模块输出为0，将NLSEF简化为线性误差反馈，公式为：

图4 基于自抗扰控制器的永磁同步电机谐波抑制算法仿真模型

令控制系统为线性定常系统，公式为：

式中，x为系统状态变量；x(n)为x的n阶导数；ai为增益系数。

将式（14）、式（15）带入式（11），经过数学推导及整理即可得出文献[15]给出的定理“一阶ADRC 关于绝对稳定零解的充分必要条件是一阶线性控制对象渐进稳定，且ADRC参数均大于零。”参考该定理可知本文所述ADRC是稳定且收敛的。

4 仿真及试验

4.1 仿真分析

根据搭建的基于自抗扰控制器的永磁同步电机谐波抑制算法仿真模型设置电机及逆变器模型参数如表1所示。电机转速为1 500 r/min，扭矩为100 N·m。

表1 永磁同步电机及逆变器参数

本文模型仿真试验主要针对该算法的抗扰性及谐波抑制的效果进行对比分析。在抗扰性对比试验中，将图4中的自抗扰控制器替换为PI 控制器作为参考对象1，再在参考对象1 的基础上安装传统非扩张状态观测器作为参考对象2。在3 组对象控制环节中分别注入-50 V 的反电动势模拟电机运行过程中机电部分可能出现的内、外扰动，结果如图5 所示。在控制环节的输入电流信号中注入1 组上限为30 A 的随机信号模拟电机控制器驱动部分可能出现的信号干扰，结果如图6所示。最后，对比PI控制器与ADRC搭配谐波抑制算法的电流波形，结果如图7所示。

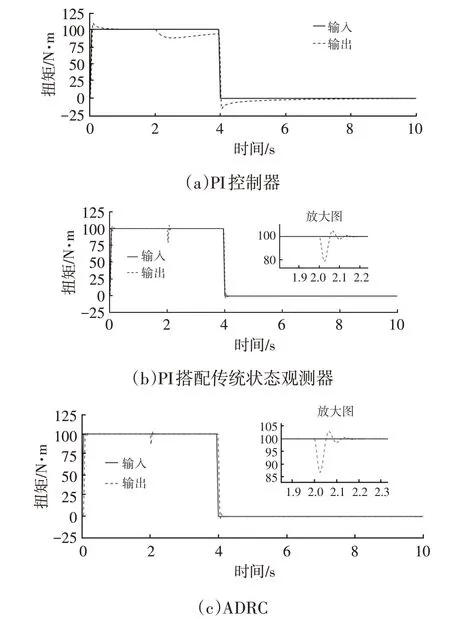
图5 注入反电动势时控制扭矩仿真结果

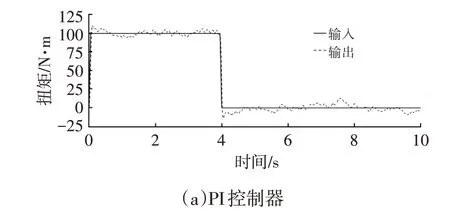
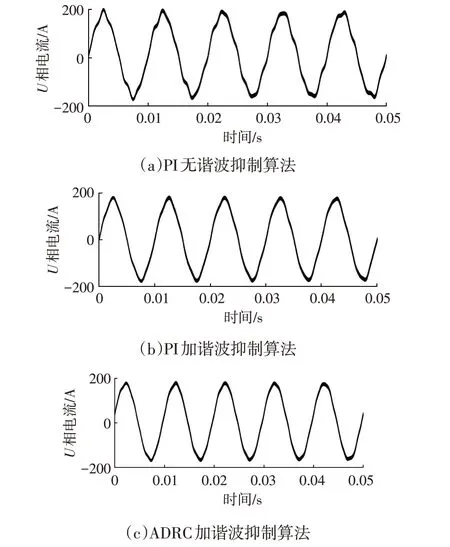
图7 谐波抑制效果U相电流仿真波形对比

由图5 可知，PI 控制器存在较长时间的稳态误差，而PI 配合非扩张状态观测器以及ADRC 都可以较快消除外部扰动，ADRC 抗干扰性更优。由图6 可知，参考对象1 和参考对象2 效果类似，波形相较ADRC 均不理想。对于谐波抑制算法，ADRC 和PI 控制器对高次谐波的抑制效果具体数据如表2 所示，ADRC 效果略优于PI。在实际调试过程中发现，PI 控制器的超调与速度存在矛盾，而谐波抑制的效果也与控制器参数强相关，在调节过程中往往顾此失彼，难以两全。反观ADRC，由于TD 模块可以对输入信号进行跟踪和滤波，起到缓冲作用，超调现象已然解决。而ESO 和NLSEF 的设计结构决定了其速度和抗扰性均优于PI的简单结构。在参数调试过程中，ADRC 基本无需考虑超调问题，对参数要求低，轻易即可使谐波抑制算法的效果优于PI 控制器。

4.2 试验验证

为进一步验证算法的可靠性，使用如图8 所示的AVL台架搭建平台进行试验。

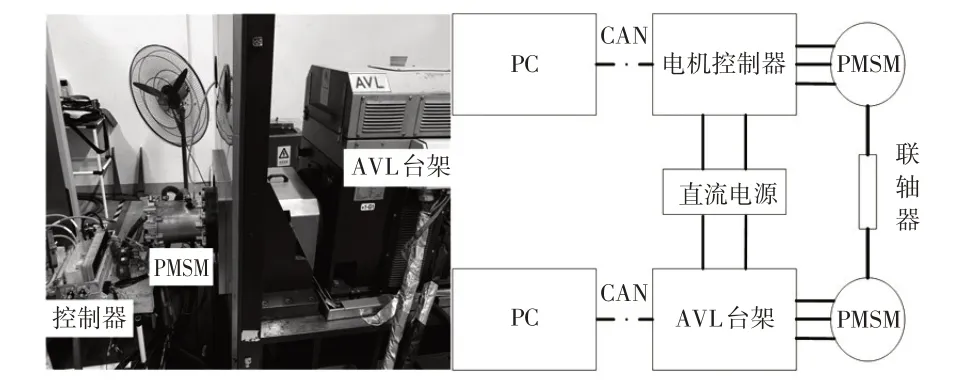
图8 试验平台及其硬件结构

考虑到台架安全性要求及受试验设备制约，无法外加反电动势模拟外部扰动，故只进行谐波抑制效果对比试验。电机控制器芯片型号为TMS570ls1115，功率开关器件绝缘栅双极型晶体管（Insulated Gate Bipolar Transistor，IGBT）型号为SKiM606GD066HD，直流电由AVL台架供应，电压330 V，其他参数与表1所列仿真参数相同。设置电机转速为1 500 r/min，扭矩为100 N·m，试验数据如表3所示，电机U相电流波形如图9所示。

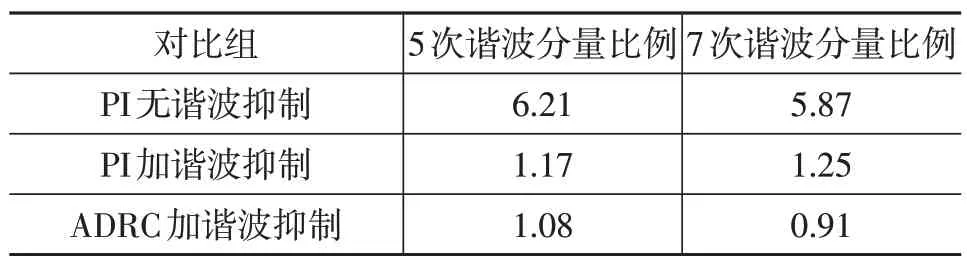
表3 U相电流谐波抑制试验效果对比 %

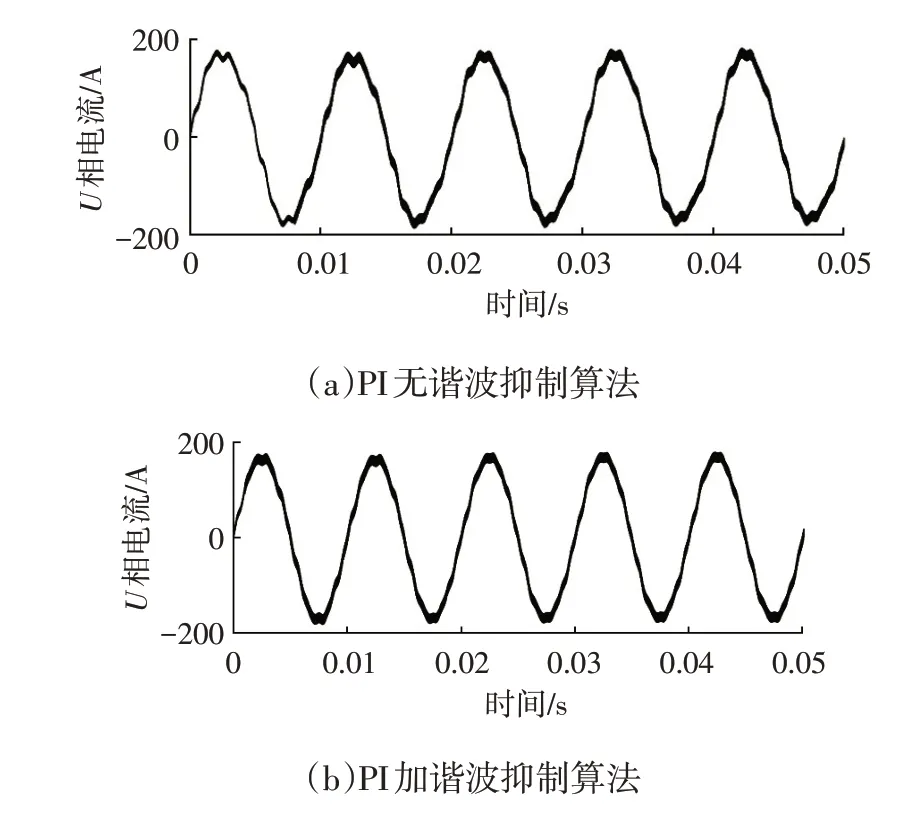
图9 谐波抑制效果U相电流试验波形对比

试验结果验证了基于自抗扰控制器谐波抑制算法策略的可行性及优越性，同时，ADRC 控制器因其抗扰能力强，对于高频次谐波也可起到一定的滤波效果。

5 结束语

本文用ADRC 控制器替代PI 控制器在永磁同步电机电流环中的作用，并结合谐波抑制算法对电机电流中的5、7 次谐波进行补偿修正，仿真和试验结果表明，ADRC控制器可以很好地实现传统PI控制器的功能，同时，ADRC 控制器使系统抗干扰能力更强，谐波抑制效果更优，参数调节更易。