基于预测滑转率的转矩分配策略研究＊

刘涵 李涛 聂彦鑫 谢宁

（中国汽车技术研究中心有限公司，天津 300300）

1 前言

轮毂电机驱动系统将中央驱动系统的传动装置集成在车轮上，省去了差速器、传动轴等传动部件，具有体积小、可控自由度较高、易于布置等优势，成为纯电动汽车驱动系统的发展方向[1-2]。

轮毂电机驱动的电动汽车取消了传统机械差速器，故需对左、右驱动轮的转矩进行协调控制，以维持转向和驱动过程中车辆的稳定性。目前，国内外在该领域的研究主要分为2类：一是基于滑转率反馈自适应系统进行电子差速控制，如文献[3]～文献[7]等对驱动轮反馈的纵向滑转率进行分析，采用模糊PID 控制、神经网络控制、滑模变结构控制等自适应控制对驱动轮的输出转矩进行自适应调整，但由于行驶路面复杂多变，输出的转矩往往根据当前的滑转率对上一时刻输出转矩进行调整，这种控制方法存在部分控制滞后的问题；二是基于路面识别设计的差速系统，如文献[8]～文献[10]等通过线性最小二乘法或者逻辑门限的方法对路面特征值进行识别，然后根据最优滑转率对转矩进行调整，这种方法能够根据路面情况得到最优输出转矩，在控制过程中有较强的主动性。本文综合上述研究方案的特点，提出一种基于预测算法对转矩进行自适应分配的方法，并通过仿真及硬件在环（Hardware-In-the-Loop，HIL）测试对动态转矩分配系统进行验证。

2 车辆模型

本文以某小型纯电动SUV 样车为研究基础，其驱动系统构型如图1所示。整车由集成在后轮上的2个轮毂电机输出扭矩驱动，整车参数如表1所示。

图1 驱动系统构型

表1 整车参数

控制系统构型如图2所示，整车控制器（Vehicle Con⁃trol Unit，VCU）计算电机转矩输出值，并通过动力CAN（Powertrain CAN，P-CAN）将需要输出的信号传输至2个驱动电机控制器（Motor Controller Unit，MCU），四轮安装的转速传感器将转速信号通过CAN总线传输至VCU。

图2 控制系统构型

在车辆转向过程中，左、右驱动轮产生载荷差，外侧车轮载荷增加，内侧车轮载荷减小，且转向角越大、车速越快时，这种现象越明显[11]。而当路面情况相同时，载荷越大，可以分配的驱动转矩越多。因此，本文根据驱动轮载荷的不同进行第一次转矩计算。

考虑到非簧载质量和路面坡度角的影响，对左、右驱动轮的载荷进行多自由度车辆动力学分析：

式中，FZL2、FZR2分别为左、右后轮的载荷；FZR为车辆在纵向坡度角为ΦR、横向坡度角为0的路面上行驶时后轴的负载；Fms为后轴簧载质量在转向过程中引起的载荷偏移；FTR为转向过程中悬架产生恢复力矩造成的载荷偏移；Fmus为非簧载质量在转向过程中产生的载荷偏移。

因为使用轮毂电机代替中央驱动电机后，非簧载质量增加较多，故该部分载荷偏移量必须予以考虑[12]，则驱动轮载荷主要分为FZR、Fms、FTR、Fmus4个部分：

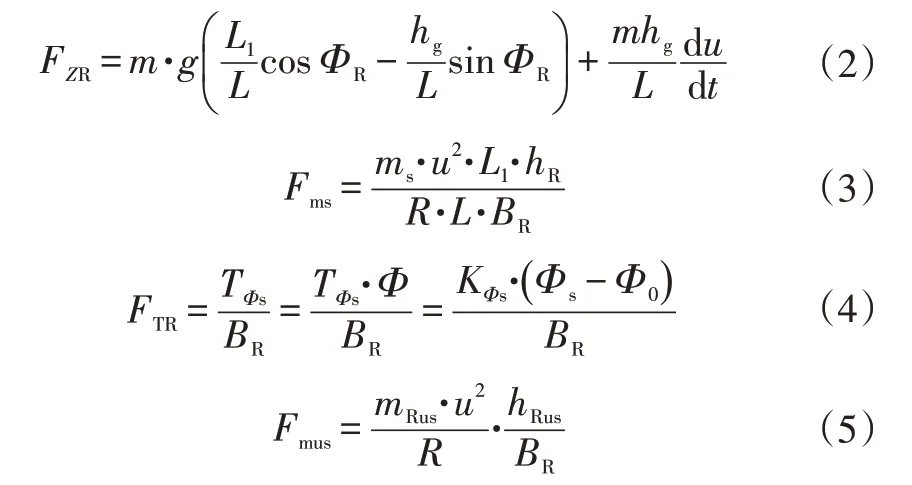
式中，g为重力加速度；u为车辆沿前进方向的行驶速度；hR为后轴承载悬挂质量的质心高度；BR为后轮距；R为当前车辆状态下的转向半径，可由阿克曼转向模型及转向盘转角计算得出；TΦs为侧倾力矩；Φ为车辆与水平面之间的侧倾夹角；Φs为行驶过程中车身的侧倾角；Φ0为路面横向与水平面之间的夹角；KΦs为车身后悬架的侧倾刚度；mRus为后轴非悬挂质量；hRus为后轴非悬挂质量的质心高度，为方便计算，取为后轴驱动轮滚动半径r。

车辆动力学模型如图3 所示，其中，MR为质心到地面的垂直距离。

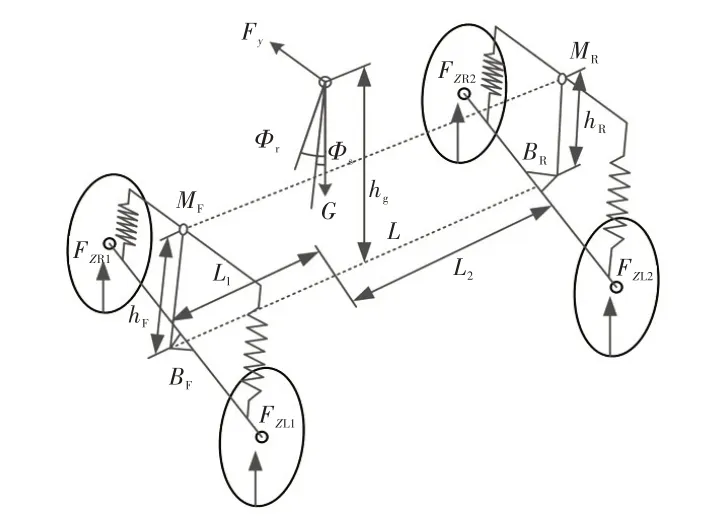
图3 车辆动力学模型

3 后轮驱动转矩分配

本文设计的转矩分配策略如图4所示，首先根据驱动轮载荷初步分配转矩，预测的滑转率经粒子群优化（Particle Swarm Optimization，PSO）算法寻优计算得出左、右后轮输出转矩修正参数αL2、αR2，并将其与初步分配的转矩相结合，得出驱动电机应输出的最终转矩，该转矩信号经P-CAN 输出至MCU，MCU控制驱动电机进行使能，至此完成整个系统的优化输出。

3.1 按载荷分配驱动轮转矩

纯电动汽车多采用踏板模拟器代替传统燃油车的机械式油门踏板。电子油门踏板输出的电压为0～5 V[13]，只需将该电压信号KT通过AD 采样转换便能计算得出当前油门踏板的开度，利用输出扭矩拟合曲线可以计算得出驾驶员对动力系统需求的总转矩TE。

图4 整车驱动控制示意

车辆转向时左后轮与右后轮的垂直载荷之比C为：

按驱动轮载荷分配扭矩的结果为：

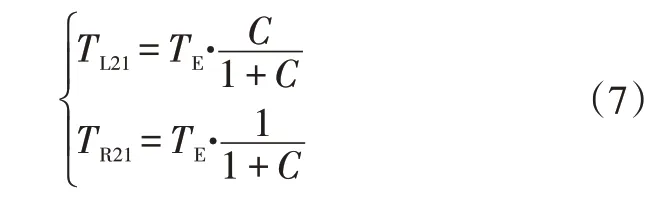
式中，TL21、TR21分别为第一次分配得到的左、右后轮输出转矩。

3.2 驱动转矩修正

后轮驱动转矩的第一次分配只是根据驱动轮负载按比例分配，以避免负载轻的驱动轮输出转矩过大造成车轮滑移率过大。但实际行驶工况下路面情况复杂多变，为充分利用地面附着力，需要确定路面特性修正转矩的输出，使车轮运行在最优滑转率附近，以充分利用地面附着力，提高车辆的经济性和稳定性[14]。

Burckhardt等提出的μ-S曲线可准确描述不同路面下车轮滑转率S与路面附着系数μ的函数关系[15]：

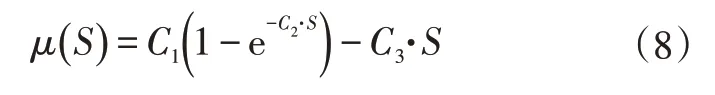
式中，C1、C2、C3为拟合曲线特征值。

特征路面上的最优滑转率Sp及最大路面利用附着系数μ(Sp)分别为：

7种常见特征路面的特征值如表2所示[15]。

通过识别驱动轮所接触路面的附着系数及滑转率，并根据表2中的Sp及μ(Sp)使用T-S模糊算法识别出当前路面的类型，最后给出最优滑转率及最大路面利用附着系数。路面观测系统[8]输出驱动轮所处路面的最优滑转率分别为SL2、SR2。

在以往该领域的研究中，多数基于当前滑转率反馈修正的方法进行控制。因此，本文提出预测滑转率的方式对转矩进行修正，以提高该系统的实时性。

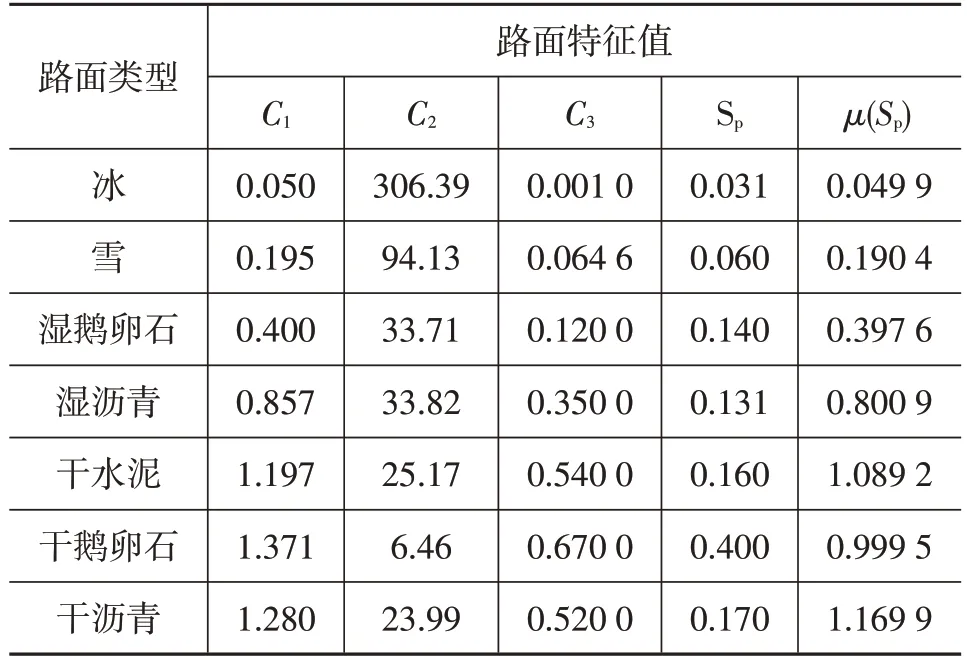
表2 7种路面的拟合曲线特征值

本文根据1/4 车辆动力学模型[16]预测驱动轮滑转率。以左后驱动轮为例，在左前轮和左后轮处安装霍尔转速传感器，测量左前、左后轮的实时转速ωL1、ωL2。在驱动行驶过程中，有：

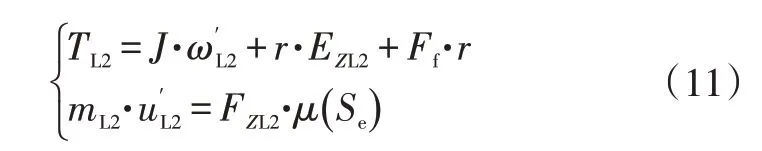
式中，J为驱动车轮总成的转动惯量；Ff为轮胎的滚动阻力，可通过台架测试得出；为1/4车辆模型中负载的悬挂质量。

在传感器采样周期内输出转矩不变的情况下，预测下个采样点驱动轮的转速及行驶线速度：

式中，ueL2、ωeL2分别为采集计算的实时速度和转速。

在采集左后驱动轮行驶线速度时，由于后驱动轮会出现滑转现象，直接测量计算存在较大误差，因此，在左前轮安装转速传感器，由实时采集的左前轮转速ωeL1利用阿克曼转向模型[17]（见图5）计算得到左后轮在行驶过程中的线速度ueL2：

而左后驱动轮的转速可以通过安装在车轮制动盘附近的霍尔转速传感器直接测量得出。

在积分计算完成后，根据式（13）中的转速及行驶速度计算预测下一采样点的驱动轮滑转率：

同理可得到右侧驱动轮的预测滑转率SR2F。

图5 阿克曼转向模型

从上述滑转率的预测过程中可以看出，随着路面条件的变化，最优输出转矩是非线性随机的优化目标，使用常规固定参数控制器控制时，系统的鲁棒性过低。粒子群优化算法凭借其易实现、参数较少、无需解码编码等优点，被许多领域的专家学者广泛采用[18-19]，因此，本文选取粒子群优化算法进行自适应寻优计算。

本文采用粒子群优化算法的目标为优化输出的最优转矩与下一报文周期输出的扭矩的比值，即αL2、αR2。为加快搜索速度，并且考虑到驱动防滑控制系统与驾驶员对转矩需求的主导关系，将粒子群搜索的范围设置为(0.2≤αL2＜1]∪(0.2≤αR2＜1]。

粒子群优化算法在寻优起始阶段，将粒子随机分布在整个搜索区间内，每次迭代后，更新每个粒子的搜索方向以及局部、全局搜索到的最优值：

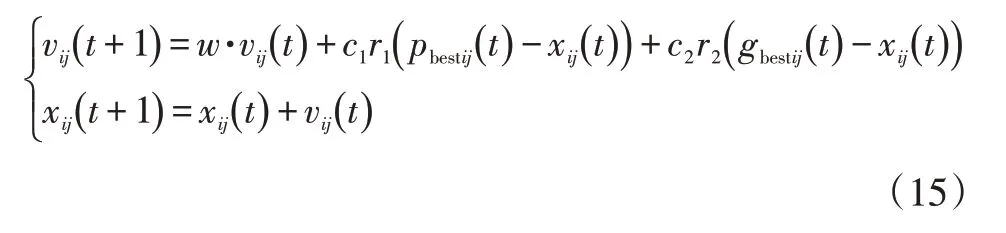
式中，w、c1、c2为固定的权重因子，本文分别设置为0.8、2、2；vij为单个粒子在搜索空间中的速度；pbestij为单体粒子寻优历史中搜索到的个体最优解；gbestij为全部种群中搜索到的全局最优解；r1、r2为(0,1)范围内的随机数。

粒子所在位置的优劣根据适应度函数进行判断。为了同时优化2个驱动轮的滑转率，适应度函数选取为2个预测滑转率与最优滑转率差值的均方根值：

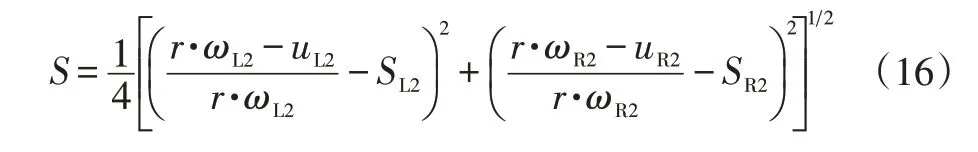
粒子群优化算法需要计算出满足最小适应度函数的目标值，并输出最优的粒子坐标。

经过粒子群优化算法寻优计算，得出2个转矩调整系数，并计算得出最优输出转矩：

考虑到汽车运行的复杂工况，计算得出的驱动电机转矩可能超过轮毂电机输出转矩的上限，因此增加计算扭矩的限制模块，即计算得出的扭矩超过轮毂电机的最大转矩时，设置优化系统的最终输出值为轮毂电机的最大扭矩，程序框图如图6 所示。图中TL2L、TR2L为经过判定之后由总线输出到MCU的扭矩值。

图6 扭矩限制监测模块

4 转矩分配策略仿真测试

首先在多变附着条件的路面上对本文设计的转矩分配算法进行仿真。在260 m的水平道路上，设置最优滑转率分别为0.17、0.13、0.17，对应长度分别为80 m、80 m、100 m的3段测试路面。优化前、后的滑转率曲线如图7所示，车辆直线行驶速度如图8所示，直线行驶过程中驱动轮输出的转矩曲线如图9所示。

图7 优化前、后驱动轮滑转率

图8 优化前、后行驶速度

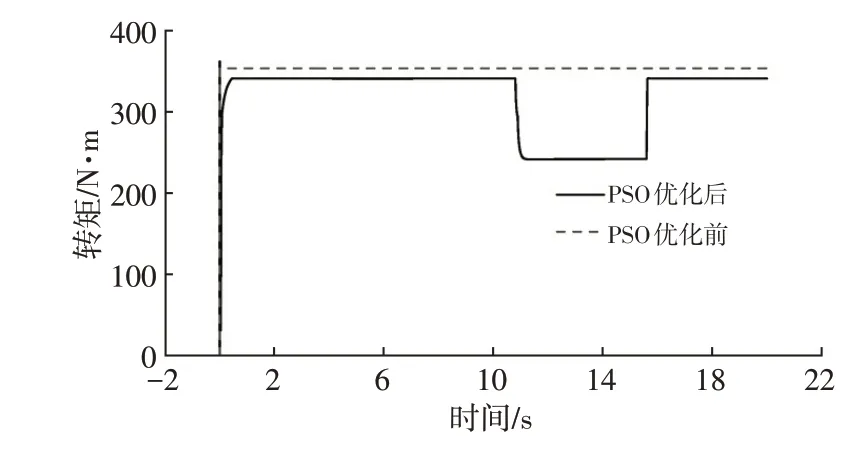
图9 优化前、后驱动轮驱动转矩

从仿真测试结果可得：本文提出的转矩优化分配算法可以在附着条件多变的路面上减小驱动轮的滑转率，提高行驶安全性；优化分配后的滑转率基本保持在最优滑转率附近，有更高的路面利用附着系数，可以提升整车的动力性。

多变附着条件路面仿真后，设计固定附着条件路面上双移线工况仿真，将路面最优滑转率设置为0.13。为突出转矩分配及优化性能，设置车辆从静止开始起步，油门踏板开度为0.7，沿标准双移线路径行驶。仿真结果如图10～图12所示。

图10 优化前、后驱动轮滑转率

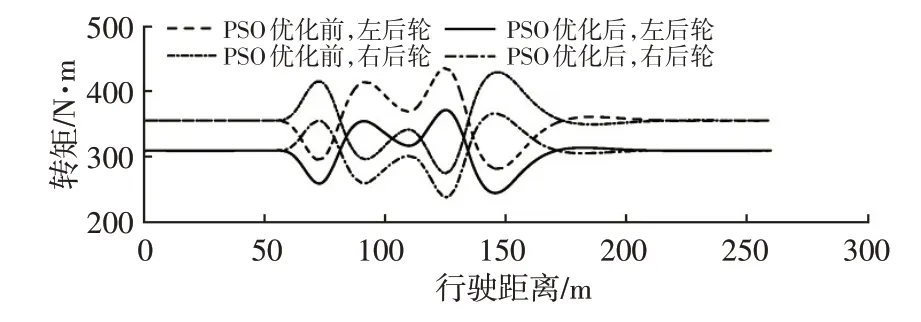
图11 优化前、后驱动轮输出转矩

图12 优化前、后行驶速度

分析双移线工况仿真测试结果可知：本文设计的转矩优化分配算法在转向过程中同样可以有效控制左、右驱动轮的输出转矩，并将驱动轮的最大滑转率由0.175 降至0.140 附近，贴近该路面上最优滑转率，获得了最大的路面利用附着系数；降低驱动轮滑转率可以提升整车的驾驶稳定性，提高路面利用附着系数可以提高动力性。

5 HIL验证分析

在目标样车的网络架构中，转矩输出功能设置在VCU 中。本文设计的优化分配算法计算量较大，故使用Infineon TC 265D 处理器搭建VCU 硬件，该控制器为32 bit双核处理器，可满足处理器计算能力的需求，如图13所示。

在整车行驶过程中，转矩优化分配计算所需要的转速信号经过P-CAN传输至VCU，优化计算完成后，VCU将转矩信号经P-CAN 传输至MCU，达到调整驱动电机输出转矩的目的。

图13 调试中的VCU

HIL 测试 时，选用dSPACE 的ASM Vehicle Dynamics Model 车辆动态模型搭建测试场景模型，进行HIL仿真测试，如图14所示。

图14 VCU硬件在环测试系统

本文利用HIL测试进行了双移线工况测试，测试场景同仿真测试中双移线测试场景。同时，作为对比，选择将PSO优化转矩输出部分代码直接删除，将基于车辆动力学计算的转矩直接输出给HIL 测试设备作为转矩优化前的对比数据。HIL测试结果如图15～图17所示。

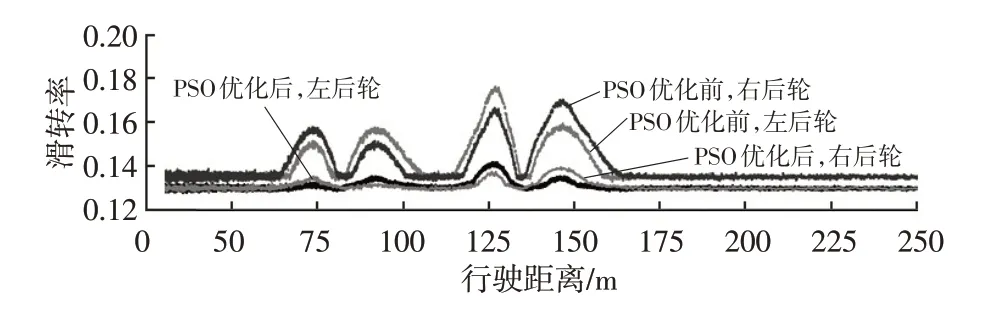
图15 优化前、后驱动轮滑转率

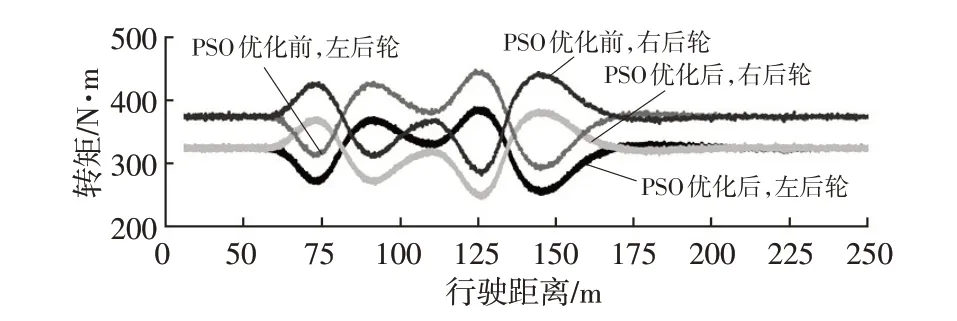
图16 优化前、后驱动轮输出转矩

图17 优化前、后驱动轮输出转矩

由HIL测试结果可知，虽然HIL测试结果与仿真测试结果的驱动轮输出转矩有所偏差，但是在忽略硬件信号传输及采集噪声误差的情况下，PSO 在硬件平台上同样可以实现优化转矩分配的功能，在相同的测试条件下，能够比仅依靠车辆动力学计算得出的转矩更贴近行驶路面的最优滑转率，并在减少转矩输出的同时获得更大的路面附着系数，较好地实现电子差速及优化转矩输出的功能，提高车辆运行过程中的经济性和驾驶稳定性。

6 结束语

本文在分析整车力学模型的基础上，进行了驱动轮转矩的分配。在初步分配后，预测计算下一报文周期的驱动轮滑转率，并使用粒子群优化算法对该非线性优化目标进行寻优计算，计算得出下一报文周期最优的输出转矩。多变附着条件路面及固定附着条件路面双移线工况仿真结果表明，本文设计的算法可以很好地控制转矩输出，并将滑转率控制在最优滑转率附近，以获得最大的路面附着系数。在此基础上使用Infineon TC265D搭建整车控制器，并进行了HIL测试，结果显示，本文设计的算法在硬件平台上同样能实现设计的优化功能，增强车辆的驾驶操控稳定性和行驶安全性。