某重型卡车后挡泥板支架断裂分析及优化

黄 玮，陈淑平

某重型卡车后挡泥板支架断裂分析及优化

*黄 玮1,2，陈淑平1,2

（1.江铃汽车股份有限公司产品开发技术中心；2.南昌市工业技术研究院，江西，南昌 330052）

在进行 45 000 km 耐久试验过程中，某重型卡车样车后轮后挡泥板右侧断裂。基于 Nastran 的频率响应分析对该挡泥板进行仿真分析，找出断裂失效的原因；基于变密度法的拓扑优化方法，优化后得出不同的密度云图，根据密度云图所示材料分布，合理布置加强筋的位置。改进后的方案制作样件进行路试检验，顺利通过了45 000 km耐久试验，挡泥板右侧无断裂现象，由此表明了改进措施能够有效的解决挡泥板断裂问题。

后挡泥板; 频率响应分析; 拓扑优化

0 引言

某重型卡车样车后挡泥板在 45 000 km 耐久试验中，发现右后挡泥板出现明显开裂，从图1可以清晰观察到。若该车投放市场，将会引起顾客抱怨，影响市场竞争及销售。经故障还原分析确定挡泥板是共振失效，针对挡泥板系统必须采取措施，解决共振问题。本文对该问题分析和解决过程进行了系统阐述。

图1 失效照片

1 开裂故障分析

该车挡泥板安装管梁受布置空间限制，需要伸出很长的悬臂梁，很容易引起后挡泥板抖动。振动容易会引起疲劳耐久和共振失效，因此需要确定失效方式，再找到失效原因。为了找出断裂失效的原因，可以采用先进的有限元方法进行仿真，考虑通过频响方法进行分析。结合仿真结果和路谱测试结果分析，清晰看出最大应力位置（见图2）与实际断裂位置（见图1）相同，并且最大应力位置处频率与路谱峰值处吻合。可以基本确认后挡泥板断裂失效是共振引起的，由于挡泥板系统本身悬臂梁的缺陷，导致很难从加长挡泥板连接支架、挡泥板加强筋、管梁变厚及增加挡泥板安装点等结构优化来提升挡泥板频率。因此需要改变挡泥板的模态频率，来避开共振频率。故考虑从挡泥板本身进行优化设计来避开共振频率（见图3）。

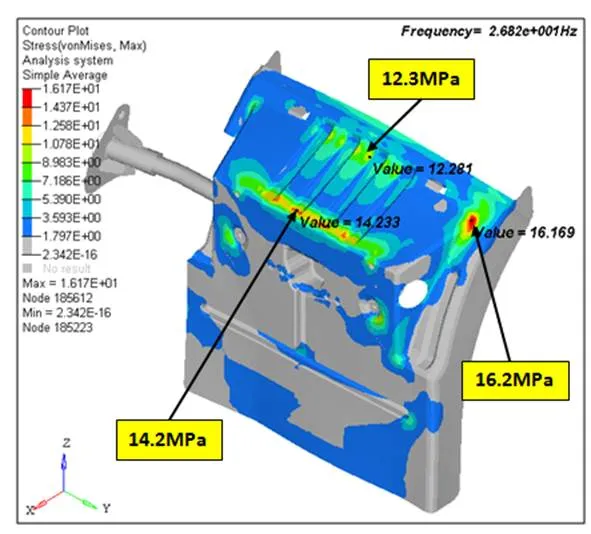
图2 后挡泥板处应力云图

图3 后挡泥板共振问题解决流程图

2 有限元模型的建立

2.1 有限元网格划分

挡泥板系统三维模型见图4。应用 HyperMesh[1-2]软件进行几何清理和网格划分。由于主要考察后挡泥板的受力状态，只要对挡泥板系统模型进行计算。网格大小为 5 mm，单元类型为CTRIA3、CQUAD4、CTETRA和CHEXA。支架和挡泥板的材料性能见表 1。采用主机厂通用有限元软件 MSC Nastran 进行数值计算。

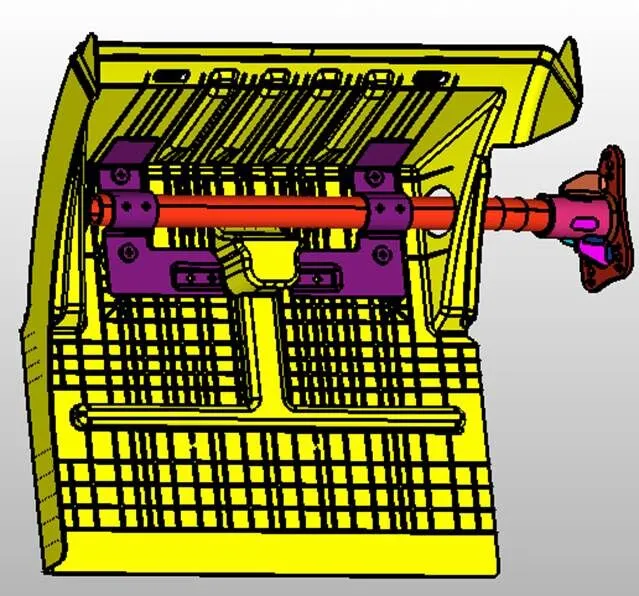
图4 后挡泥板三维数模

表1 支架和后挡泥板材料参数

2.2 边界条件

后挡泥板响应主要激励来源于车架（X方向0.6g，Y方向0.25g，Z方向0.9g）。为考察后挡泥板的响应情况，故把激振点放置在挡泥板支架与车架连接的的安装点上，完全约束X/Y/Z三个方向的转动及平动，见图5。

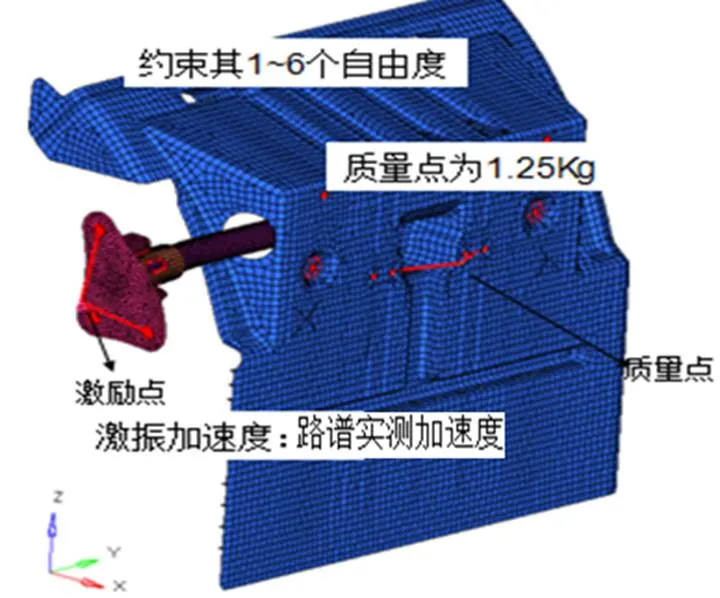
图5 有限元模型

3 有限元分析结果

3.1 模态实验和计算结果

在后挡泥板的激励点建立约束，约束其6个自由的，再提交Nastran[3-5]中进行模态计算，采用HyperView中浏览相应的模态振型，其结果见图6。

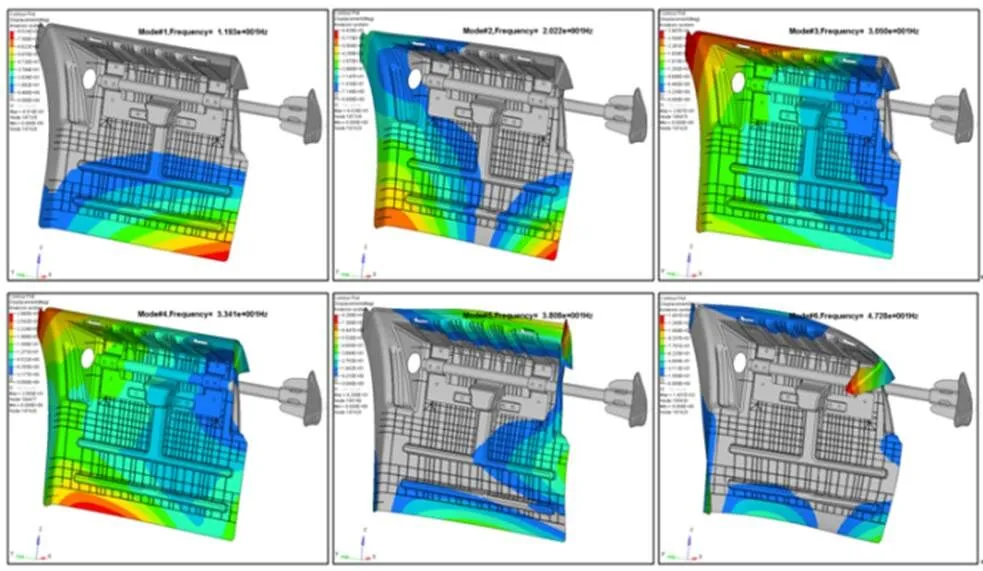
图6 后挡泥板初始模型的前6阶模态振型

参照后挡泥板的模态实验结果，以验证模型的正确性，试验值与计算值对比如表2所示。通过锤击产生脉冲激励，实验采用单点激励，逐一拾取响应点信号的方法，实验结果如图7所示。

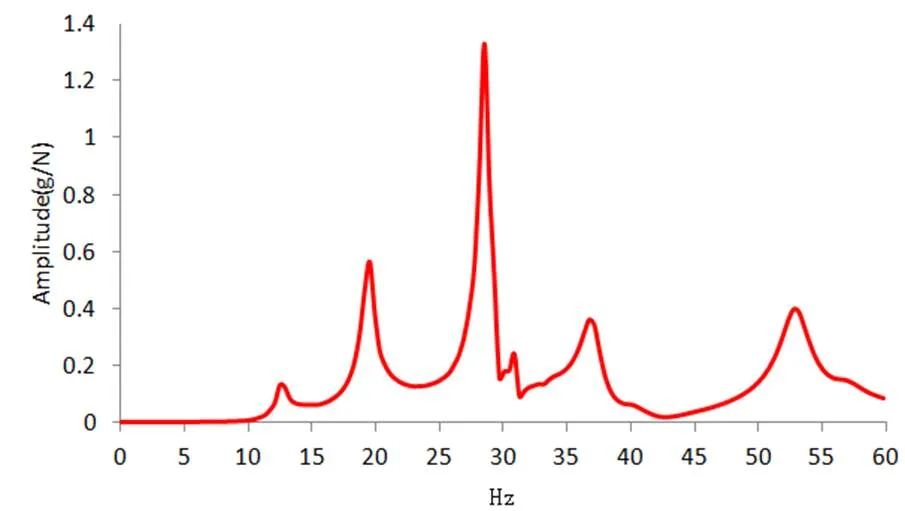
图7 后挡泥板初始模型的测试结果

表2 后挡泥板试验值与计算值对比表

从表2可以看出试验结果和有限元分析结果基本吻合，误差仅在5%以内，表明有限元分析的结果可靠，同时验证建立的分析有限元模型正确性。

3.2 频响分析结果

在耐久试验中，在挡泥板支架上贴振动加速度传感器，测出各方向的实际道路加速度，用于后挡泥板x，y和z向进行的频率响应分析[3]，来考察后挡泥板在各向的频率响应水平，计算结果见表3。

表3 后挡泥板的频率响应结果

路谱测试结果中，13Hz和28Hz时附近有加速度峰值出现，与仿真计算结果的响应频率较吻合。路谱测试结果见图8

图8 路谱测试

根据，和向模态频响仿真和路谱测试结果，判断z向振动是引起后挡泥板断裂主要激励源。为确保安全因数，此后分析分别对x向和z向进行模态频响分析。

后挡泥板响应最大是在z向26.8 Hz频率激励下，在12.1 Hz附近也有峰值出现。为重现后后挡泥板失效模式，对其进行x，y和z向同时激励的频响分析，激励加速度为1 g。有限元分析结果见图2和图9。频率为26.8 Hz时，后挡泥板开裂处在1 g加速度荷载激励下最大应力为16.2 MPa，接近材料的屈服强度。仿真结果的最大应力位置就是断裂位置，并且失效点位置最大应力均发生在26.8 Hz频率下，与路谱峰值处频率吻合。后挡泥板失效是由于共振引起的，需改变后挡泥板模态频率，避开共振频率。为解决挡泥板开裂问题，需改进后挡泥板z向刚度;后挡泥板开裂处应力很大，有应力集中现象，需要对该件结构进行优化设计。

图9 x向后挡泥板处应力云图

4 提出改进方案并计算

4.1 建立拓扑优化模型

结构拓扑优化[6-8]的基本原则是将寻求结构的最优拓扑问题转化为在给定的设计区域内寻求最优材料分布的问题，可以理解为“最大刚度”设计，结构拓扑优化实质是材料的删减。由于挡泥板根据要求设计，其厚度不能低于3.5 mm，确定挡泥板加强筋的分布，就不能直接通过拓扑优化得到，需要转变一下思路:将挡泥板的厚度由原先的3.5 mm增加到12 mm，然后在这12 mm的基础上进行拓扑优化设计，删减材料直至挡泥板的厚度不小于3.5 mm。这样就可以在质量不增加很多的情况下，又保证了厚度不低于3.5 mm，实现挡泥板的拓扑优化设计。

为了满足该覆盖件的刚度条件，以第一阶固有频率最大化为目标函数，以体积分数(质量)小于等于0.4为约束条件，建立挡泥板的拓扑优化设计模型:

Find:X=(x1,x2,…,xn)

Maximize:Frequency 1

Subject to:KU=F

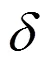
在HyperMesh中设置好设计变量、响应函数、约束变量和目标函数后，提交OptiStruct[9-10]进行拓扑优化，整个优化过程经历8步迭代，优化后的单元密度云图如图9所示，优化过程中前6阶固有频率变化如图10所示。

通过图10挡泥板优化后的单元密度云图，可以初步确定加强筋布置位置。密度值为1的位置对应在密度图上的浅色区域应该布置加强筋，密度值为0.001的位置对应密度图上的深色区域不需布置加强筋；由图11可知，在拓扑优化过程中其前四阶固有频率不断提高。

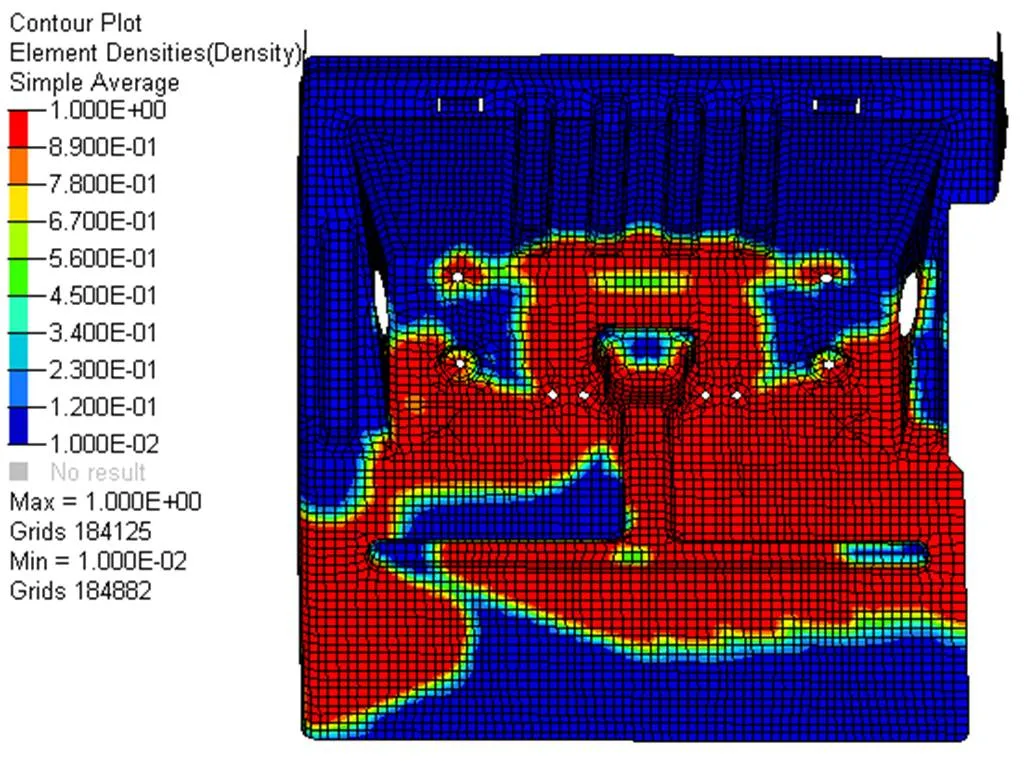
图10 挡泥板优化后的单元密度云图

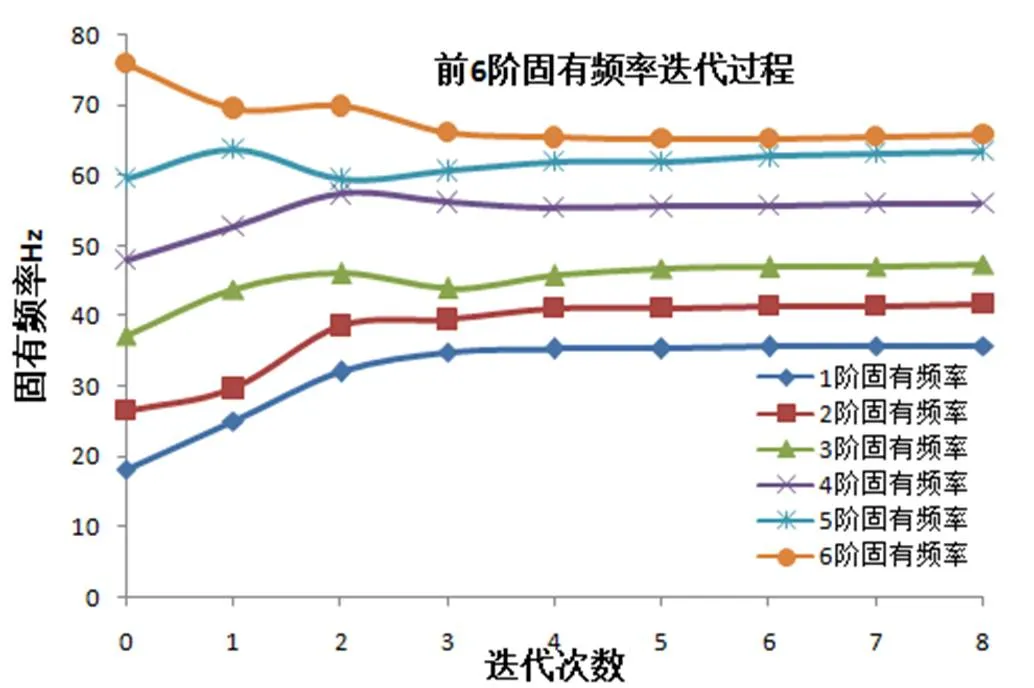
图11 前6固有频率迭代过程

4.2 拓扑优化后模型的重建与频响分析

优化后的最优拓扑结构不仅只考虑到结构的刚度，而且还需要满足制造工艺、装配关系等设计要求。根据优化结果以及实际制造经验抽象成的布置加强筋后的挡泥板实体模型如图12所示，图中白色结构为所布置的加强筋。新的挡泥板结构中，未布置加强筋的部分厚度仍为3.5 mm，而布置加强筋的厚度则为12 mm，加强筋宽度为1.3 mm。

图12 拓扑优化后重建的挡泥板模型

在HyperMesh中对新建的挡泥板模型进行网格划分，设置好各项参数，对改进方案进行模态分析及x和z向的频率响应分析，计算结果分别见图13-图15。

图13 后挡泥板初始模型的前6阶模态振型

图14 改进方案x向后挡泥板处应力云图

Fig.14 Stress nephogram of improved scheme x at rear fende

图15 改进方案z向后挡泥板处应力云图

Fig.15 Stress nephogram of improved scheme z at rear fende

表4 后挡泥板初始与优化模型对比表

由表4可知，后挡泥板的各阶固有频率均有提升，优化后挡泥板的刚度提升；质量则由2.897 kg增至3.093 kg，只增加0.196 kg,质量变化不是很大。在重量增加很小的情况下，该拓扑优化后的挡泥板刚度提高了，避开共振频率，达到了设计要求。

改进方案最大应力出现在23 Hz附近，后挡泥板最大应力为14.98 MPa，根据路谱测试数据(图7)在23 Hz处对应的加速度峰值很小。故在实际工况中，改进方案后挡泥板处受力会更小。判断该改进方案能够满足耐久测试要求：

5 结束语

基于先进的有限元技术，重现后挡泥板故障失效模式，优化方案制作挡泥板样件，并实车通过耐久路试，因此得到以下结论。

(1)采用频响方法进行故障还原，并确定失效方式及失效原因，为故障整改提供方向；

(2)模态分析结果表明，其前六频率与模态试验误差率在5%以内，优化后的前六阶模态频率均得到提升；

(3)采用拓扑优化对其结构进行优化，分析结果表明，密度图上的浅色区域刚度不够，需要布置加强筋；

(4)采用优化方案进行耐久实车测试，顺利通过了45 000 km耐久试验；

(5)该方法能能够有效支持工程问题的解决，为同类工程问题的解决提供了一种新的思路。

[1] 张胜兰. 基于HyperWorks的结构优化技术[M].北京:机械工业出版社,2008.

[2] Ch. Siva Rama Krishna.Simulation and Analysis of Residual Stresses in a Laminated Graphite/Epoxy Composite Plate Using HyperMesh[M]. Springer : Springer Singapore, 2019

[3] 马爱军,周传月,王旭.Patran和MSC Nastran有限元分析专业教程[M].北京:清华大可学出版社,2005.

[4] 杨剑,张璞,陈火红. MD MSC Nastran有限元实例教程[M].北京:机械工业出版社,2008.

[5] 熊伟,余显忠,黄晖.基于MSC Nastran的后保险杠频率响应分析[J]. 计算机辅助工程,2015, 25(6):87-89.

[6] 伍新,吴晨曦.非正态分布的连续体结构可靠性拓扑优化方法研究 [J].机械设计及制造,2019,15(8):62-66.

[7] 许华旸,关立文,王立平,等. 惯性载荷下飞行模拟器大臂结构的拓扑优化[J]. 机械工程学报,2014,50(9): 17-23.

[8] 刘成颖,谭锋,王立平,等.面向机床整机动态性能的立柱结构优化设计研究[J]. 机械工程学报,2016,52(3): 161-168.

[9] 刘伟,张志斌,刘清颖.基于OptiStruct的机身前段总体优化设计[J].机械设计及研究,2013,29(5 ): 30-33.

[10] 宋雪梅,罗永俊,张兴琦. 基于OptiStruct的制动卡钳拓扑优化设计[J]. 机械设计,2018,35(1 ):200-202.

Fracture problem and topology optimization analysis for rear fender of a Heavy truck

*HUANG Wei1,2, CHEN Shu-ping1,2

(Product Development&Technology Center,Jiangling Motors Corporation Limited, Nanchang Industrial Research Institute ，Nanchang,Jiangxi 330052,China)

During the 45 000 km road durability test of a heavy truck vehicle，the fracture problem occured on the rear fender. The frequency response of the rear fender was simulated and analyzed by Nastran，and the fracture problemwas found. Based on variable density method of the topology optimization method, the different density maps were obtained, and the location of the reinforcement was reasonably arranged according to the material segment. The improved scheme of the prototype made the road test, successfully passed the 45000 km endurance test, found no fracture phenomenon at the right fender, which indicated that the improved measures could solve the problem of fender fracture effectively.

rear fender,frequency response analysis, topology optimization

U469.2

A

10.3969/j.issn.1674-8085.2020.04.013

1674-8085(2020)04-0065-06

2019-11-11；

2020-02-03

*黄 玮(1989-），男，江西南昌人，中级工程师，硕士，主要从事汽车设计及分析工作(E-mail:394431063@qq.com);

陈淑平(1989-)，女，江西临川人，助理工程师，主要从事汽车设计及分析工作(E-mail:823697718@qq.com).