光波偏振态的相干矩阵表示及变换的研究

黄 艳

光波偏振态的相干矩阵表示及变换的研究

黄 艳

（漳州职业技术学院电子工程学院，福建，漳州 363000）

为从物理本质上揭示光波偏振态、偏振的叠加、混合和传播等概念和应用，利用相干矩阵方法分析光波偏振态。深入探讨了几种特殊意义情况下光波相干矩阵的特点及其可能的合成方式。选择部分偏振态通过线性光学元件和以布儒斯特角入射介质分界面时透射光偏振特性分析的典型例子，揭示了光波偏振态的变换问题。并在邦加球中以图解形式表示光波偏振态的几种合成形式及相干矩阵传输前后的偏振态变换。图解法使物理量的代数表示几何化，能更形象地描述偏振态的物理意义。分析表明，完全描述光波的偏振特性需要相干矩阵的本征值和本征态共同表征。

物理光学；偏振态；相干矩阵；偏振度；邦加球；本征值

0 引言

近年来，随着激光技术的发展，光学的应用范围急剧扩大，其中偏振光技术作为一种重要的测量手段越来越受到人们的重视[1-5]。面对偏振光技术日新月异的发展，需对偏振光知识有本质的理解，如何描述光的偏振态及变换是偏振光技术应用的基础。目前，大学众多光学教材中对光的偏振现象的描述主要是从现象出发的定性描述，然后以两个波叠加为基础的定义，强调通过两波的位相差来区分各种类型光的偏振状态[6-7]。其好处在于直观形象、便于理解，不足之处是对自然光、完全偏振光和部分偏振光的本质区别、偏振的各向异性等概念极不清楚。

如所周知，光的相干性起源于光辐射的随机性导致诸参与叠加光波相位差的随机性。偏振的多样性也是来自于光源辐射的随机性，只是取决于二维平面上两个正交基的相位差的随机性。所以偏振的可观测量是一种统计系综描述，在二维理论中通常用相干矩阵表示，类似于统计物理学中的混态或密度矩阵，其特征之一是含糊性，即一种确定的偏振态对应的起因可以有无数种[8]。另有一种与之表示等价的是斯托克斯理论，其几何表象是三维邦加球坐标系[9]。两种方法在光学的高级教程或专著中都有详细的论述，但是很少看到具体应用的描述和例子，所以使初学者在看完理论后仍停留在抽象的概念中，不能真正理解其中的物理本质。

本文采用二维相干矩阵法详细分析了光波的偏振性质，并给出几种特殊意义情况下光波相干矩阵的特点及其可能的合成方式。选择部分偏振态通过线性光学元件和以布儒斯特角入射介质分界面时透射光偏振特性分析作为典型例子，揭示了光波偏振态的变换问题，并将光波的偏振状态的几种合成形式及传输后的变换在邦加球坐标系中以图解形式表示。图解法使物理量的代数表示几何化，让读者能够从物理本质上体会光波本征解、偏振的叠加、混合和传播等概念和应用。

1 偏振态的相干矩阵描述

矩阵光学是将数学矩阵方法应用于光学研究，对描述和解决一些繁琐的光学问题，例如几何光学计算、薄膜干涉研究等，提供了一种方便和有效的方法。1941年美国物理学家琼斯提出了用一个列矩阵来表示光矢量的两个分量的方法，这矩阵称之为琼斯矢量[10]。光学元件的传输矩阵对应地采用2×2的琼斯矩阵来表示，利用琼斯矩阵法可方便计算偏振光通过不同组合的偏振光学元件后出射光的偏振状态。然而，在涉及到部分偏振光问题时，由于琼斯矢量不能表示位相随时间变化的自然光和部分偏振光，于是又发展了二维相干矩阵，为系统分析准单色光的偏振状态提供了一种有效方法[8]。

准单色光波场矢量的变化既不是完全规则的，又不是完全不规则的，显现出部分偏振的特点。研究此类光场的偏振特性需引入相干矩阵

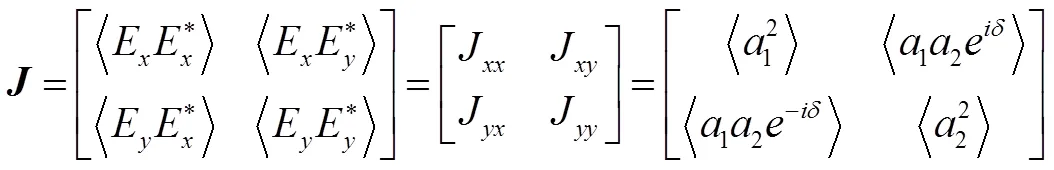
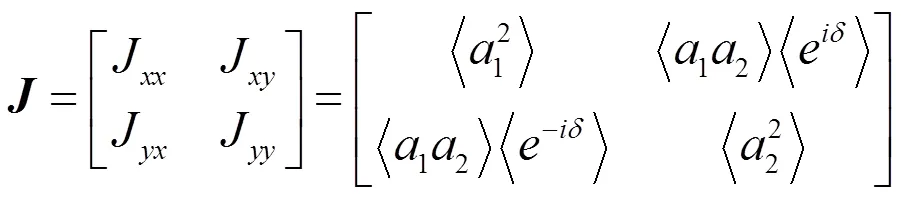
称为光波的相干矩阵，其中矩阵的迹r即其对角元之和为光的总强度

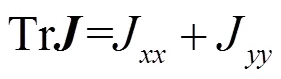
相干矩阵的本征方程可写为

现求相干矩阵的本征值，列出矩阵的久期方程为[12]

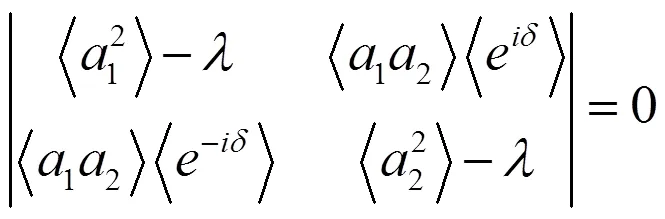
求得两个非零本征值

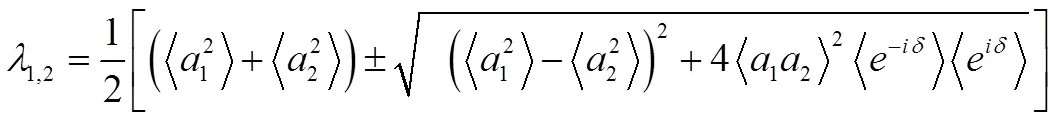
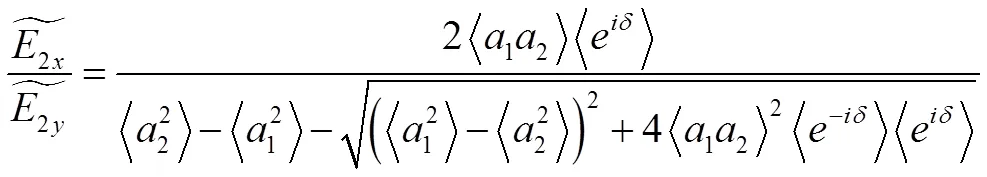
以上两式含有复量，故这对本征态一般互为正交的椭圆偏振态，在这组态基下，相干矩阵是对角化的，即

本征值与本征态的物理意义在于：本征态是描述偏振的最基础态，一定是偏振的，且属于不同本征值的本征态是正交且不相干的，相应的本征值表示光处于该本征态的强度。

现分析三种特殊意义情况下对角化相干矩阵的形式：

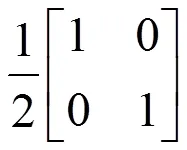
在邦加球中由球心表示。

2）当非零本征值是单根时，所对应的本征态代表完全偏振态

由邦加球面上的点表示。

例如，电矢量在方向和方向上单位强度的线偏振光矩阵分别为

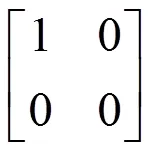
一个部分偏振态可按比例1、2分解成两个正交本征态的非相干混合，即

还可将相干矩阵写成如下形式

（15）式的物理意义是，一个部分偏振态可按特定比例分解成一个自然光与本征态的非相干混合，非相干混合即为两个偏振态的相干矩阵相加

很显然偏振度满足条件0≤≤1。

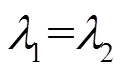
偏振度只是反映了部分偏振光中完全偏振分量所占据的权重，只由本征值决定，并没有完全描述其偏振性质。例如具有同样偏振度的两个部分偏振光，它们的本征态可以是不一样的，完全描述光波的偏振性质需要相干矩阵的本征值和本征态，后面将通过实例进行说明。

2 光波偏振特性的邦加球描述

1892年邦加（H.Poincare）提出运用邦加球分析光的偏振态，球半径代表光强大小，球面上的点代表完全偏振光；球心处表示完全非偏振光（自然光）；球内的点表示部分偏振光。下面运用邦加球分析光波的几种偏振态图示表示，这里我们仅对光波的偏振状态感兴趣，即考虑单位强度的光，因此下列图示中的邦加球均是归一化的，邦加球半径为1。

2.1 部分偏振光的混合

2.1.1 部分偏振光按本征态与自然光非相干混合

2.1.2 部分偏振光按两正交本征态非相干混合

如前所述，一个部分偏振态可按比例1、2分解成两个正交本征态的非相干混合，如(14)式所示

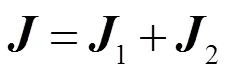
2.1.3 部分偏振光按任意两偏振态非相干混合

前面提到的相干矩阵的两种分解方式是最常见和实用的，表示两种态的非相干混合，原则上相干矩阵可以视为任意两个偏振态的非相干混合，这是相干矩阵作为统计描述的一种含糊性，因此这种分解方式可以有无数种，即

2.2 完全偏振光按两正交本征态相干叠加

完全偏振光有线偏振光、圆偏振光和椭圆偏振光，在邦加球中用球面上的每一点表示一椭圆偏振光，北半球为右旋态，南半球为左旋态，在北极和南极演化为右旋和左旋圆偏振光，赤道上退化为线偏振光。完全偏振光也可看做由一对偏振态互相正交的本征态相干叠加，这种分解方式也可以有无数种，即

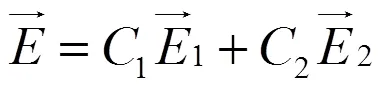
图1 光波偏振特性在邦加球中的表示

3 光波偏振态的变换

3.1 部分偏振态通过线性光学元件后的变换

偏振光学元件对偏振态改变通常是线性的，可用2×2的琼斯矩阵表示，其作用于前面所述相干矩阵，可描述部分偏振态通过线性光学元件后偏振态的改变。相干矩阵经过线性光学元件后的变换可表示为

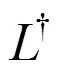
线性光学元件通常分为两大类，一类是无损耗的，如波晶片、旋光器等，其琼斯矩阵是幺正的；另一类是有损耗的，例如起偏器（包括线偏振器和圆偏振器），其琼斯矩阵是非幺正的。

3.1.1 无损光学元件

对无损光学元件而言，其琼斯矩阵是幺正的，根据矩阵代数，幺正变换不改变本征值，但一旦经过变换则会改变相干矩阵和本征态。以快轴在方向的1/4波片为例，它将入射光的相干矩阵1改变为出射光的相干矩阵2，即

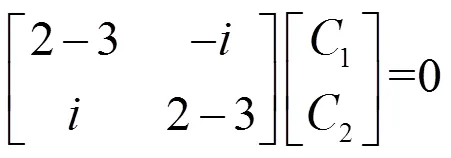
本征态经快轴在方向的1/4波片后的变化如下

可见1/4波片使得左右旋圆偏振态变成了旋转了±45°的线偏振态。

从以上例子可以看到，入射光和出射光的本征值均相等，因此偏振度经过1/4波片前后保持不变。但从分析可知入射光和出射光的偏振特性完全不一样，因经过1/4波片后改变了部分偏振光的本征态。因此，完全描述光波的偏振性质需要相干矩阵的本征值和本征态。

3.1.2 有损光学元件

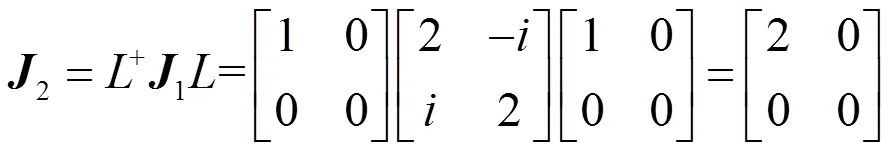
从（24）式可见，输出光为电矢量在方向的线偏振态0，由于偏振滤波作用光的总强度减小了。上述两种部分偏振态通过光学元件的情况在邦加球上表示如图2所示，其中

（晶体快轴在x轴方向、线偏振器透振方向在x轴方向）

3.2 布儒斯特角入射介质分界面时透射光的偏振特性

3.2.1 自然光入射

当自然光以布儒斯特角i入射在介质1和介质2的分界面上时，此时与入射面平行的分量100%透过，因此反射光中只有与入射面垂直的s分量，则反射光为线偏振光，其相干矩阵

设波的振幅反射率为，透射光为部分偏振光，其相干矩阵

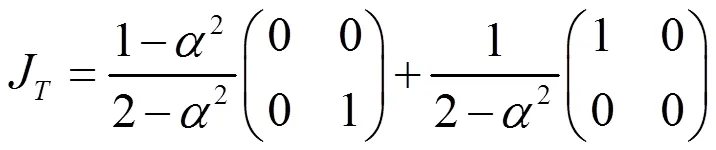
3.2.2 圆偏振光入射

式中，分别为琼斯矢量在该正交基底中的坐标分量。其在邦加球中的图解如图3（b）所示，其中，。

4 结论

本文论述偏振光的二维相干矩阵理论，并将光波的几种偏振状态在邦加球坐标系中以图解形式表示。图解法使物理量的代数表示几何化，能更形象地描述偏振态的物理意义，如部分偏振态的非相干混合、偏振态的叠加和部分偏振态经线性元件的传输变换等。文中辅以几个典型例子说明相干矩阵、本征态和相应图解法的构造、求解和应用。关于部分偏振光的几个结论。

1）完全偏振态在邦加球表面，由两个独立参数决定；在邦加球球内的点表示部分偏振光，由3个独立参数决定；邦加球球心处，表示完全非偏振光（自然光）；

2）一对正交偏振态（在邦加球任直径两端）的非相干混合是部分偏振态（杠杆法则），相干叠加是偏振态（直角三角形法则）。

3）与偏振态的矢量分解类似，以相干矩阵表述的部分偏振态的分解有无数种方式，但重要的是按本征态分解，或者按自然光与本征值较大的态分解。

[1] 孙仲秋,赵云升,阎国倩,等. 利用偏振光技术计算海水密度的深入研究[J].学学报,2010,30(8): 2451-2457.

[2] 王玉波,杨江涛,唐军,等. 基于大气偏振光的航向角探测系统[J].兵器装备工程学报,2019,40(3):127-131.

[3] 张志刚,毛亮,程腾,等.利用消杂散光的偏振光技术提高光学读出红外成像检测灵敏度[J].红外与毫米波学报,2013,32(4):331-336.

[4] 马号,熊剑,郭杭,等. 基于大气偏振光特性辅助定向的自主导航方法[J].应用光学,2016,37(2):162-167.

[5] 于洵,杨烨,姜旭,等. 基于偏振光谱成像的目标识别方法研究[J].应用光学,2016,37(4):537-541.

[6] 姚启钧.光学教程[M].北京:高等教育出版社,2002: 304-317.

[7] 赵凯华. 新概念物理教程:光学[M]. 北京：高等教育出版社,2004:270-276.

[8] 玻恩M,沃耳夫E.光学原理(下册)[M].黄乐天,陈熙谋,陈秉乾,译.2版. 北京:科学出版社,1981:721,728.

[9] 廖延彪.偏振光学[M].北京:科学出版社,2003:52-56.

[10] 钟锡华.现代光学基础[M]. 北京:北京大学出版社，2003:427-430.

[11] 李高明,邱怡申. 传统偏振光检验法的局限性及其修正[J].福建师范大学学报:自然科学版,2012,28(6): 56-59.

[12] 上海交通大学线性代数编写组. 线性代数[M]. 北京:高等教育出版社,1991:162-172.

Research on Coherence Matrix Representation and Transformation of Polarization State of Light Waves

HUANG Yan

（Electronic Engineering Department,Zhangzhou Institute of Technology, Zhangzhou,Fujian 363000,China）

In order to reveal the polarization state of light waves, the superposition, mixing and propagation of polarization from the physical essence, the coherent matrix method is used to analyze the polarization state of light waves. The characteristics of light wave coherence matrices in several special cases and their possible synthesis methods are discussed in depth. Through the typical examples of partially polarized states passing through linear optical elements and the examples of analysis of polarization characteristics of transmitted light when incident at the Brewster angle, the transformation of the polarization state of light waves is revealed. Several synthetic forms of polarization of light waves and the polarization state transition after coherent matrix transmission are graphically represented in Poincare sphere. The graphical method makes the algebraic representation of physical quantities geometric and describes the physical meaning of polarization more vividly. It is shown that the eigenvalues and eigenstates of the coherence matrix are needed to fully describe the polarization characteristics of light waves.

Physical optics; The state of polarization; Coherence Matrix; Degree of polarization; Poincare sphere; Eigenvalue

O436.3

A

10.3969/j.issn.1674-8085.2020.04.004

1674-8085(2020)04-0014-07

2020-01-15；

2020-04-01

漳州市自然科学基金项目（ZZ2019J24）.

黄 艳(1983-)，女，福建闽清人，讲师，硕士，主要从事光学晶体偏振特性及偏光器件设计方面的研究(E-mail:huangyan_013@126.com).