tanh函数法及其在Joseph-Egri方程中的推广和应用

李 萍 白 羽

tanh函数法及其在Joseph-Egri方程中的推广和应用

*李 萍1白 羽2

（1周口技师学院文化基础课部，河南 周口 466000 2周口师范学院数学与统计学院，河南 周口 466000 ）

在齐次平衡原则的基础上探讨了tanh函数法及其一种推广的tanh函数法的具体解方程的步骤，应用Joseph-Egri方程进行具体求解，得到了在不同情况下不同结果的精确解。

齐次平衡原则；tanh函数法；推广的tanh函数法；Joseph-Egri方程；精确解

0 引言

在现实生活当中，由于非线性偏微分方程的广泛应用[1]，而引发对此研究的热潮。而tanh函数法[2]是在齐次平衡法[3]的基础之上，解非线性偏微分方程的孤立波解，可以借助它来解Ginzburg-Landau-方程[4]和修改的IBq方程[5]。但是在解题的过程中，发现了它的局限性，由此产生后来推广的tanh函数法[6]。而对于推广的tanh函数法，在解sine-Gordon方程、KDV方程的新式解[7]以及非线性发展方程(组)的行波解[8]时，可以达到用tanh函数法所不能达到的效果。本文将以同一个Joseph-Egri方程为例，分别用tanh函数法和推广的tanh函数法解出它的精确解，去直观地展示不同的精确解。

1 tanh函数法

对于非线性微分方程，假定其一般形式为

第2步：引入一个独立的新变量

即有：

第3步：假设方程可以得到tanh函数多项式如下形式的解：

由此根据齐次平衡原则，将平衡方程中的最高阶非线性项的幂次与线性最高阶导数项的幂次相等，可确定参数。

2 推广的tanh函数法

3 基于tanh函数法的Joseph-Egri方程求解

对于Joseph-Egri方程

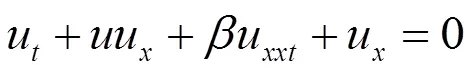
对于双曲正切函数

又因为

于是方程(3.2)的解为

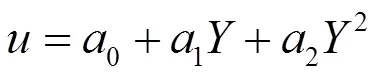
得到Joseph-Egri方程的精确解为

图1 时，的波形图

4 基于推广的tanh函数法的Joseph- Egri方程求解

现在继续考虑Joseph-Egri方程

并且令方程的解为如下形式

对于双曲正切函数

又因为

于是可以得出方程(4.2)的解为

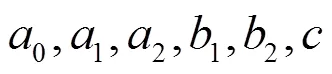
所以得到Joseph-Egri方程的精确解为

图2 β＝3时， u的波形图

由图1和图2进行直观地对比，tanh函数法比推广的方法更局限，从两个波形图就可以看出，只从x-质点坐标定下时与u-位移联系来看，用tanh函数法会使解的形式更加的单一，会使一部分解丢失。而推广的方法相对于原来的tanh函数法能解出更多丰富的解，从而更加的有优势。

5 总结

本文是在利用齐次平衡原则的基础上，先是通过tanh函数法求Joseph-Egri方程，从而求解出Joseph-Egri方程的精确解，然后为了进一步研究不同形式下的孤立波解，应用推广形式下的tanh函数法求解Joseph-Egri方程。虽然求解过程相较于tanh函数法更为复杂，但由于考虑了更精确解的情况，得到了在各种不同类型下的解的情况。

[1] 盖立涛，非线性偏微分方程的几类求解方法的探究及应用[D].呼尔浩特:内蒙古工业大学，2015:10-11.

[2] 焦向莉.Tanh函数展开法和CRE方法在非线性偏微分方程中的应用[D].宁波:宁波大学,2015.

[3] 廖雨,呼家源.齐次平衡法与Burgers-Huxley方程的精确解[J].宝鸡文理学院学报，2014(4):32-36.

[4] 李自田. LIZi-tian.经由tanh-函数法和[G'/G]-扩展法的Ginzburg-Landau-方程的新的精确同宿波和周期波解[J].黑龙江大学自然科学学报,2011,28(1): 67-71.

[5] 范凯.修改的广义Riccati方程有理展开法求解非线性演化方程[D].沈阳:东北大学，2014:14-24.

[6] 刘雪梅,接贤.利用推广的Tanh函数法求解两个非线性发展方程[J].中国民航大学学报, 2015(4):46-49.

[7] 林府标，张千宏.广义tanh函数法中Riccati方程和sine-Gordon方程的新解及其新应用[J].工程数学学报,2020(1):52-57.

[8] 额尔敦布和,特木尔朝鲁,白玉梅.利用改进的扩展tanh函数方法求解非线性发展方程(组)的行波解[J].内蒙古民族大学学报:自然汉文版,2011,26(2): 125-133.

Tanh function method and its application in Joseph-egri equation

*LI Ping1, BAI Yu2

(1. Basic culture department，Zhoukou Technician College, Zhoukou, Henan 466000, China;2. School of mathematics and statistics, Zhoukou Normal University , Zhoukou, Henan 466000, China)

Based on the principle of homogeneous equilibrium, this paper discusses the steps of tanh function method and its extended method to solve the equation. By applying the Joseph egri equation to solve the equation, we get the exact solutionsofdifferentresultsindifferent situations.

homogeneous equilibrium principle; tanh function method; extended method; Josephegrie quation;exact solution

Q175.23

A

10.3969/j.issn.1674-8085.2020.04.002

1674-8085(2020)04-0006-04

2020-02-15；

2020-04-08

*李 萍(1966-)，女，河南周口人，高级讲师，主要从事偏微分方程精确解的研究(E-mail:604799880@qq.com);

白 羽(1995-)，女，河南信阳人，主要从事微分方程的研究(E-mail:1085643931@qq.com).