基于差分麦克风阵列的恒定束宽波束形成研究

张 敏，潘 翔

(浙江大学信息与电子工程学院，浙江 杭州 310027)

0 引 言

麦克风阵列广泛应用于语音增强和语音识别领域。频率不变的固定波束形成器可以在所有频率上实现恒定的波束宽度，从而降低信号失真[1]。与自适应波束形成器相比，具有更低的计算复杂度[2]。基于离散傅里叶变换的谐波嵌套阵列是一种传统的恒定束宽方法，在每个子阵列中，阵列间距相等，通过使用不同的阵列间距和具有不同数量的子阵列使得嵌套阵列在感兴趣的频率范围内具有相似的空间响应[3]。但是，这种方法需要阵列数目很大，而且每个子阵列的波束仍然是频率相关的。差分麦克风阵列(Differential Microphone Arrays，DMA)在处理宽带信号方面有许多优点[4]。DMA能实现小孔径阵列(阵列间距要远小于波长)，具有良好的频率不变性、较强的指向性。传统的DMA存在白噪声增益(White Noise Gain,WNG)较低的问题，先实现DMA陷零点结构再最大化WNG可以改进其性能[5]，在此基础上，本文提出分两个阶段优化的Two-Stage鲁棒性差分麦克风阵列波束形成算法，分析了DMA波束形成算法对语音可懂度的提升效果，良好的恒定束宽效果减少了语音的失真，提高了在噪声干扰环境下的鲁棒性。

1 差分波束形成设计

设计N阶差分滤波器至少需要N+1个阵元，最多可以设计N个陷零点[4]。假设有1个含有M(M≥N+1)个阵元的线性阵列，阵间距为δ，第m个阵元在频点ω接收到的信号经过短时傅里叶变换(Short Time Fourier Transform，STFT)后表示为

Ym(ω,l)=e-j(m-1)ω τ0cos θX(ω,l)+Vm(ω,l)

(1)

式中，j表示虚部，τ0=δ/c，声速c=340 m/s,θ表示信号方向，X(ω,l),Vm(ω,l),Ym(ω,l)分别为目标信号x(k,l)，噪声信号vm(k,l)和接收信号ym(k,l)的STFT，k表示时间，l表示帧序号，阵列响应矢量

d(ω,cosθ)=[1,e-jω δcos θ/c,…,e-j(M-1)ω δcos θ/c]T

(2)

假设在0°～180°之间有N个陷零点0°<θN,1<…<θN,N≤180°，在无失真条件下，得到约束方程

D(ω,α)h(ω)=I

(3)

I=[1 0 0 … 0]T

(4)

α=[1αN,1…αN,N]T=[cos 0° cosθN,1… cosθN,N]T

(5)

(6)

I的长度为N+1，解线性方程可以得到滤波器系数

h(ω)=D-1(ω,α)I

(7)

2 Two-Stage鲁棒性差分波束形成算法

2.1 算法原理

为了解决传统DMA在低频时白噪声增益太低的问题，在基于最大化白噪声增益(Maximization White Noise Gain，MWNG)的原则下，本文提出一种Two-Stage鲁棒性差分波束形成方法。算法将滤波器设计分为2个部分，第1步是传统鲁棒性DMA的结构，主要用来控制滤波器陷零点的位置，第2步是在MWNG原则下优化滤波器系数[5]。滤波器表达形式如下：

(8)

(9)

(10)

根据无失真约束条件可以得到

(11)

式(11)等价于

h(2,2)H(ω)dH(ω,1)=1

(12)

(13)

dH(ω,1)为长度为M-N的矢量，因此，第2步最大化白噪声增益的滤波器系数求解可以通过解决下面的问题得到

(14)

(15)

ψ(ω)为大小为(M-N)×(M-N)的Hermitian矩阵，矩阵元素值由传统DMA系数决定。可以得到第2步的滤波器系数

(16)

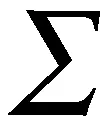
(17)

重新带入无失真约束方程得到

(18)

最后根据式(8)得到滤波器系数

(19)

2.2 性能分析

计算白噪声增益

(20)

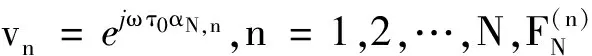
(21)

将式(18)代入式(20)计算，当σ(ω)=1-ωτ0/π得到

(22)

当ωτ0=π时，σ(ω)变成0，这时候在单位圆上有M-N-1个额外的零点；当ωτ0=0时，σ(ω)=1，第2步的滤波器就不会引入额外的零点，而且此时的WNG和未经过额外陷零处理的WNG是一样的，保证了WNG的有效性。

3 仿真与实验数据分析

3.1 仿真结果与分析

仿真实验采用阵元数M=8的均匀线阵，阵间距d=0.01，c=340 m/s，频率范围为0～4 kHz，划分为100个子带，角度范围[0°,360°]按2°等间隔划分，陷零点角度设置为106°和153°。一阶和二阶的仿真结果如图1所示。

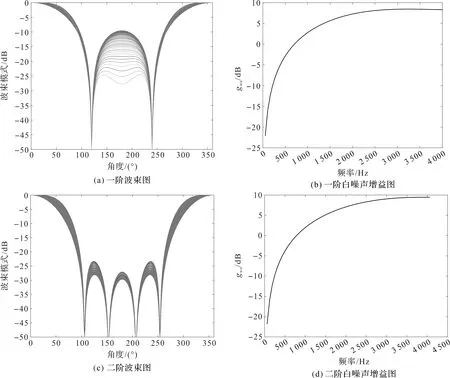
图1 仿真结果图

从图1(a)和(c)中可以看出，波束响应能大致满足频率一致性，频率一致性的下降换取了WNG性能的提升。一阶在频率低于1 kHz时，WNG小于0，二阶在频率低于1.5 kHz时，WNG低于0，故低频部分噪声的增强效果优于语音，但是，高频部分的WNG接近于常规波束形成的阵增益。阶数的增加使得频率一致性提升，但降低了白噪声增益，实际中两者要做折中处理。

3.2 实验数据处理

采用8元均匀线性阵列，阵列间距0.02 m，0°方向是目标语音信号，90°方向还有一段笑声干扰信号，时长为3 s。采用一阶差分波束形成，陷零角度90°。图2是第3通道的单通道带噪声信号的时域波形图和时频图，图3是经过一阶差分波束形成以后输出信号的时域图和时频图。从图3差分波束形成后的时频图中可以看出，高频部分的噪声能量被去除，通过主观试听，语音的清晰度和可懂度都有一定的提高，通过语音主观质量评估(Perceptual Evaluation of Speech Quality，PESQ)处理前的单通道带噪声信号的得分是1.538，差分波束形成后的得分是1.949，语音质量得到一定程度的增强。而应用低旁瓣(Frequency Invariant Beamforming，FIB)算法[6]，在波束形成输出语音质量得到同样程度提升的情况下，需要更大孔径的阵列，计算量也更大。

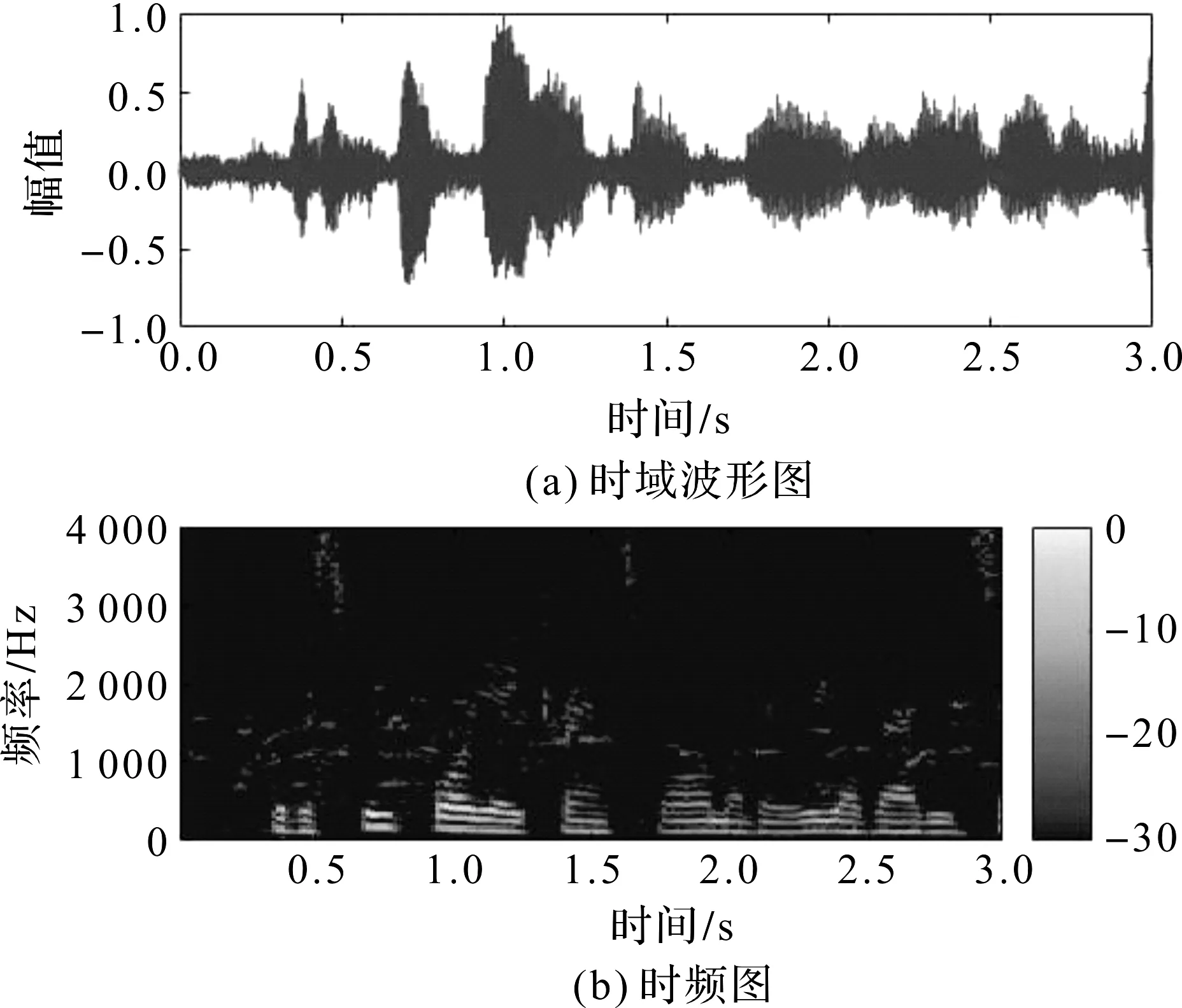
图2 单通道带噪信号

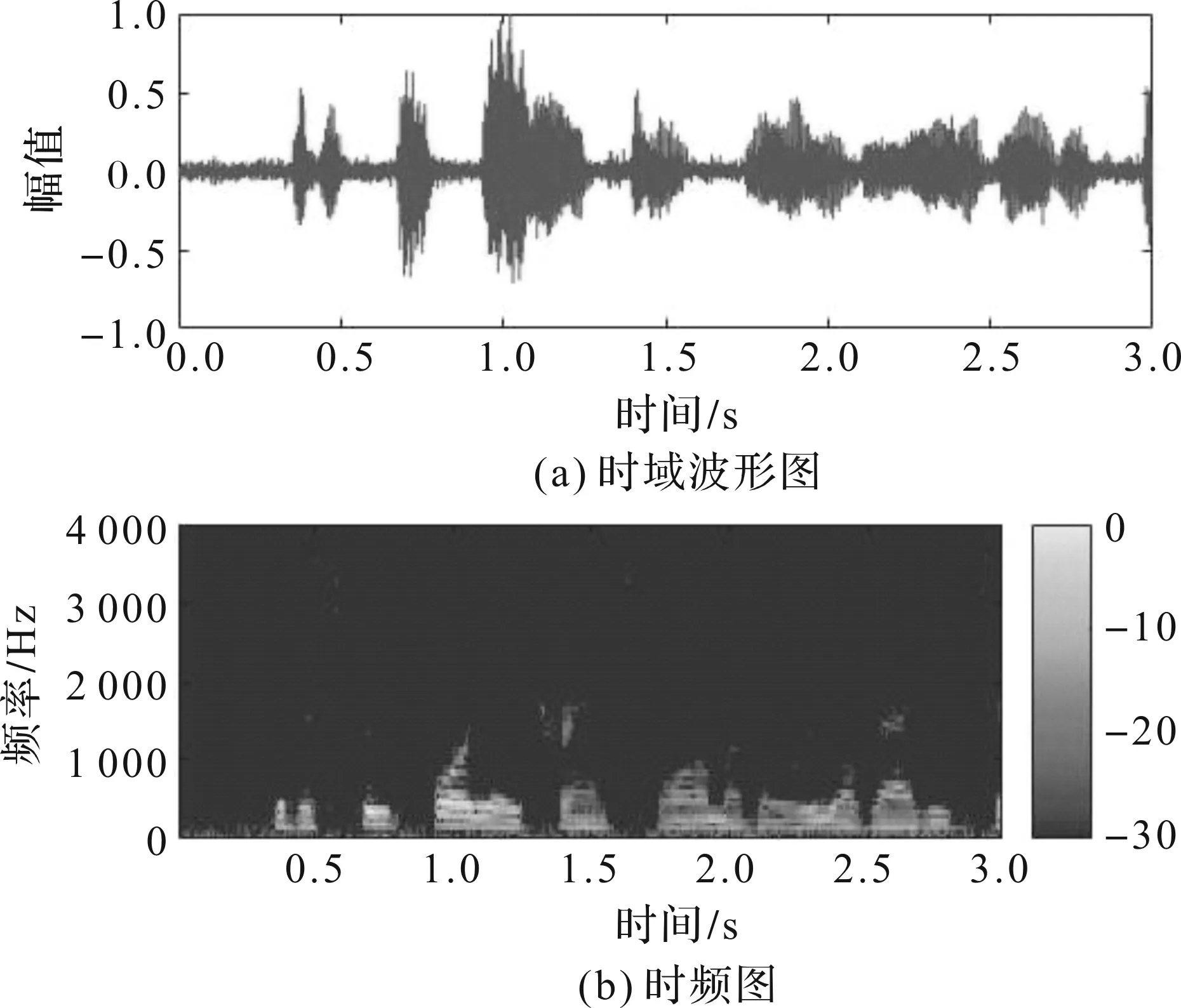
图3 差分波束形成输出信号

4 结束语

本文从传统DMA算法出发，针对传统DMA算法的低WNG和鲁棒性差等不足，提出Two-Stage鲁棒性差分波束形成算法，在保证恒定束宽的基础上，极大改善了WNG，增强了鲁棒性，在小孔径阵列中获得较好的波束响应一致性，并通过实验语音数据验证了算法的有效性。未来可以改进算法进一步提升在低频时的WNG，实现语音信号的无失真波束形成。