基于双幂次趋近律的滑模轨迹跟踪控制器设计

耿 新，孙忠廷，尚文武，柏建军,2

(1.杭州电子科技大学自动化学院，浙江 杭州 310018;2.浙江省物联感知与信息融合技术重点实验室，浙江 杭州 310018)

0 引 言

轮式移动机器人具有易于操作、机动灵活等特点，广泛应用于生活服务业、安全防御及自动化生产车间等众多领域。实际应用中，轨迹跟踪控制是研究轮式机器人运动控制的重要部分，轨迹跟踪是指移动机器人在闭环反馈控制器的作用下，从初始位置开始以期望的速度和角速度实时跟踪给定的参考轨迹。轮式移动机器人是一种典型的非完整约束系统，其具有非线性、强耦合、多输入多输出及参数不确定等特点，连续的状态反馈控制方法已经无法满足实际的轨迹跟踪控制要求[1]。另一方面，滑模控制通过控制律的切换，使系统的状态到达并维持在滑模面上，具有较好的鲁棒性和快速响应性，已广泛应用于轮式移动机器人的轨迹跟踪控制中。文献[2]在系统不受干扰的情况下，设计了一种新颖的滑模轨迹跟踪控制器，该控制器使得位置和方向跟踪误差都在有限时间内收敛到0，但是控制器输出变量存在抖振。文献[3]研究移动机器人车轮打滑情况下的运动学模型，采用自抗扰和反步控制技术对车轮打滑扰动进行估计和补偿，提高了轨迹跟踪的精度，但缺乏对车轮打滑干扰的精确估计。文献[4]通过双幂次趋近律滑模轨迹跟踪控制器来削弱抖振并克服外部干扰对系统性能的影响，提高了系统收敛速率。文献[5]将特殊幂次函数和反双曲正弦函数相结合，给出一种收敛性能和抖振均优于双幂次趋近律的新趋近律。文献[6]同时考虑运动学和动力学模型，设计了基于反步法设计轨迹跟踪控制器，但忽略了动力学模型中的不确定因素。文献[7]在存在扰动的轨迹跟踪控制系统中，运用模糊控制规则来调节快速双幂次趋近律的参数，达到较好的跟踪效果，但是系统存在抖振。上述文献研究的是移动机器人的质心与几何中心完全重合情况下的轨迹跟踪控制问题。在实际应用中，由于移动机器人结构设计、工艺制作、负载安装等导致机器人几何形状不规则、质量分布不均匀，机器人质心与几何中心是不重合的。文献[8-9]研究了移动机器人质心与几何中心不重合情况下的轨迹跟踪控制问题，但轨迹跟踪误差的收敛速度较慢。针对该问题，本文基于双幂次趋近律设计了一种新的滑模轨迹跟踪控制器，提高了轨迹跟踪系统的收敛速度。

1 运动学及轨迹误差模型

移动机器人的结构模型如图1所示。以地面为参考系建立全局坐标系XOY，以移动机器人为参考系建立移动机器人坐标系xoy，2为y轴方向2个驱动轮之间的距离，2r为驱动轮直径，d为移动机器人质心o与驱动轮轴在x轴方向的距离，θ为移动机器人行驶方向与水平方向的夹角。设在XOY坐标下给定的参考轨迹位姿坐标为参考轨迹的线速度和角速度为νr，ωr。移动机器人的实际位姿坐标为速度和角速度为ν，ω。

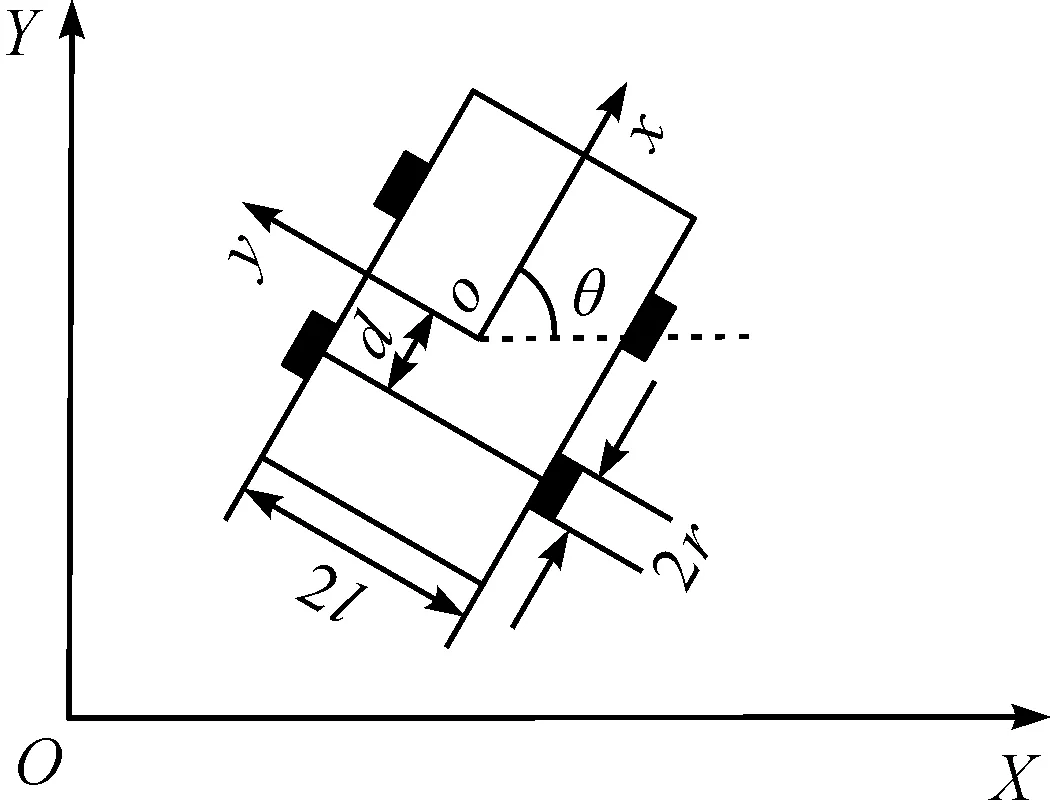
图1 移动机器人的结构模型

移动机器人的质心与几何中心不重合的情况下，当移动机器人不存在横向滑动时，移动机器人行驶方向沿着轮轴垂直方向，在轮轴方向没有速度分量时，存在如下约束方程[10]：

(1)

在式(1)约束条件下得到移动机器人的运动学模型：

(2)

移动机器人的轨迹跟踪误差模型如下：

(3)

对式(3)进行求导，结合式(2)整理可得移动机器人的轨迹误差模型：

(4)

2 快速轨迹跟踪控制器

本文的设计基于轨迹跟踪误差模型，通过选取适当的滑模面，然后基于双幂次趋近律来设计轨迹跟踪的滑模控制器，使得系统轨迹跟踪误差快速收敛到0。

2.1 控制器设计

选取滑模面s1，s2如下：

s1=θe

(5)

s2=k1xe-k2ωrye

(6)

式中，k1，k2>0，ωr≠0且为常数。对式(5)、式(6)求导得：

(7)

(8)

式(5)、式(6)满足如下双幂次趋近律：

(9)

(10)

式中，α11，α12，α21，α22>0且为常数；p11q12，p21q22，均为正奇数，sign(x)为符号函数。

联立式(4)、式(7)、式(9)得到轨迹跟踪角速度控制器：

(11)

当滑模面s1=θe在有限时间内趋于0时，得到ω=ωr。在此情况下联立式(4)、式(8)、式(10)得到轨迹跟踪速度控制器：

(12)

2.2 系统的收敛时间分析

不失一般性，假设系统初始状态si(0)>1，i=1，2，将系统从初始状态到滑模面的收敛过程分为2个阶段，第一阶段从初始状态si(0)到si=1，第二阶段从si=1到滑模面[11]。首先证明滑模面s1=θe在有限时间内趋于0。

系统从初始状态s1(0)>1到s1=1阶段，由于|s1|>1，p12/q12>1，所以系统中第二项对收敛效果起主要作用，忽略第一项，系统为：

(13)

由式(13)可得：

(14)

两边移项求定积分，得：

(15)

由式(15)解得系统从初始状态s1(0)>1到s1=1的时间为：

(16)

由于忽略了系统中趋近律的第一项，故滑模面s1=θe在第一阶段的实际收敛时间小于t1。

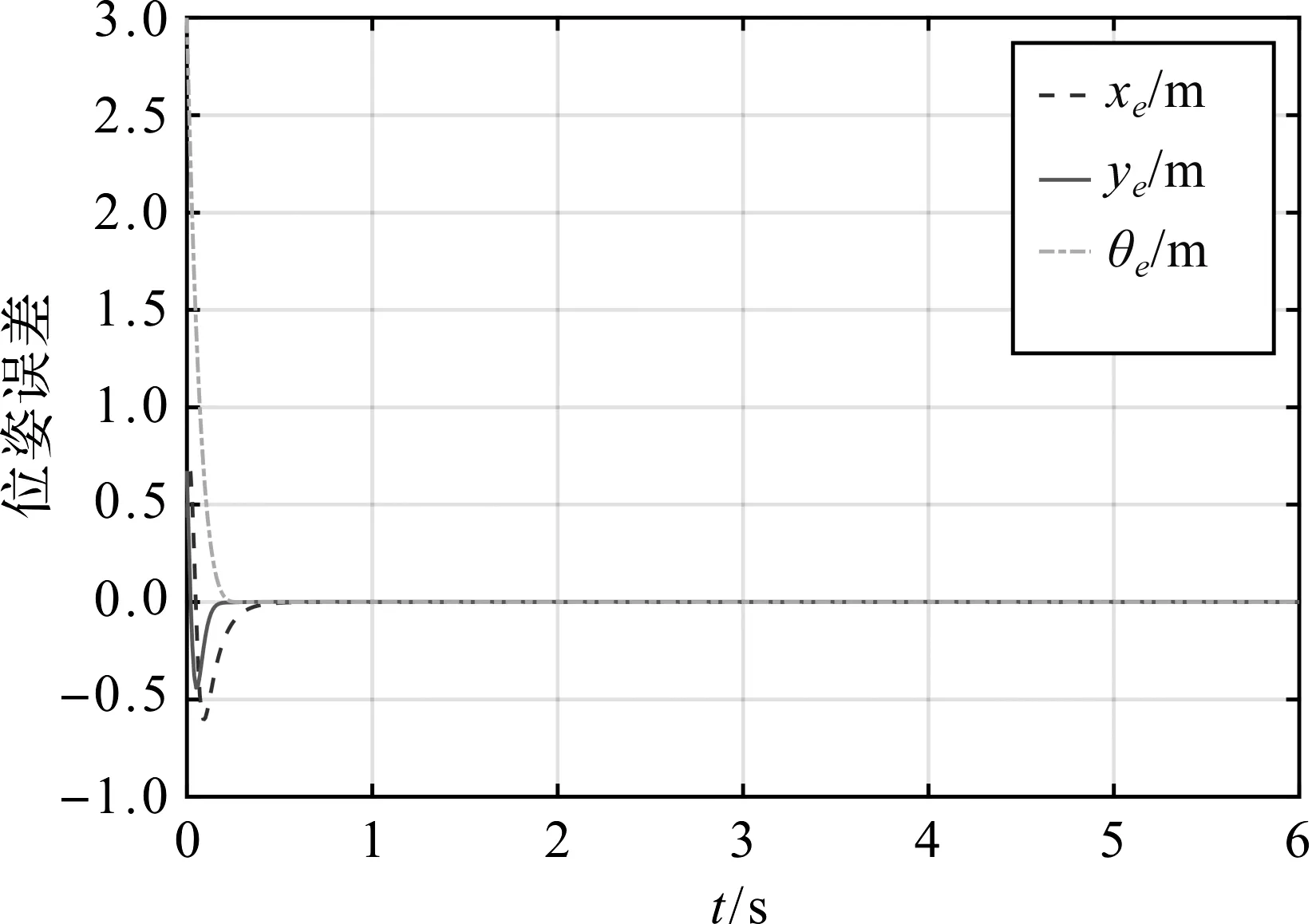
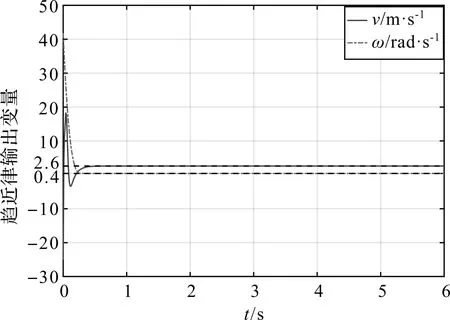
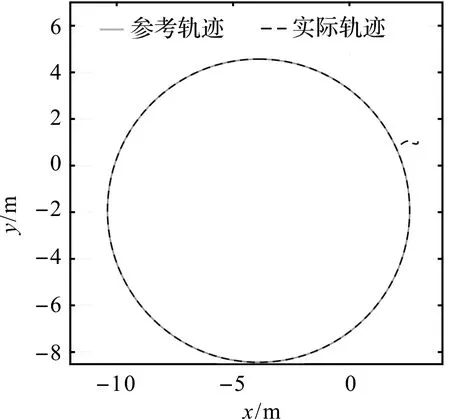
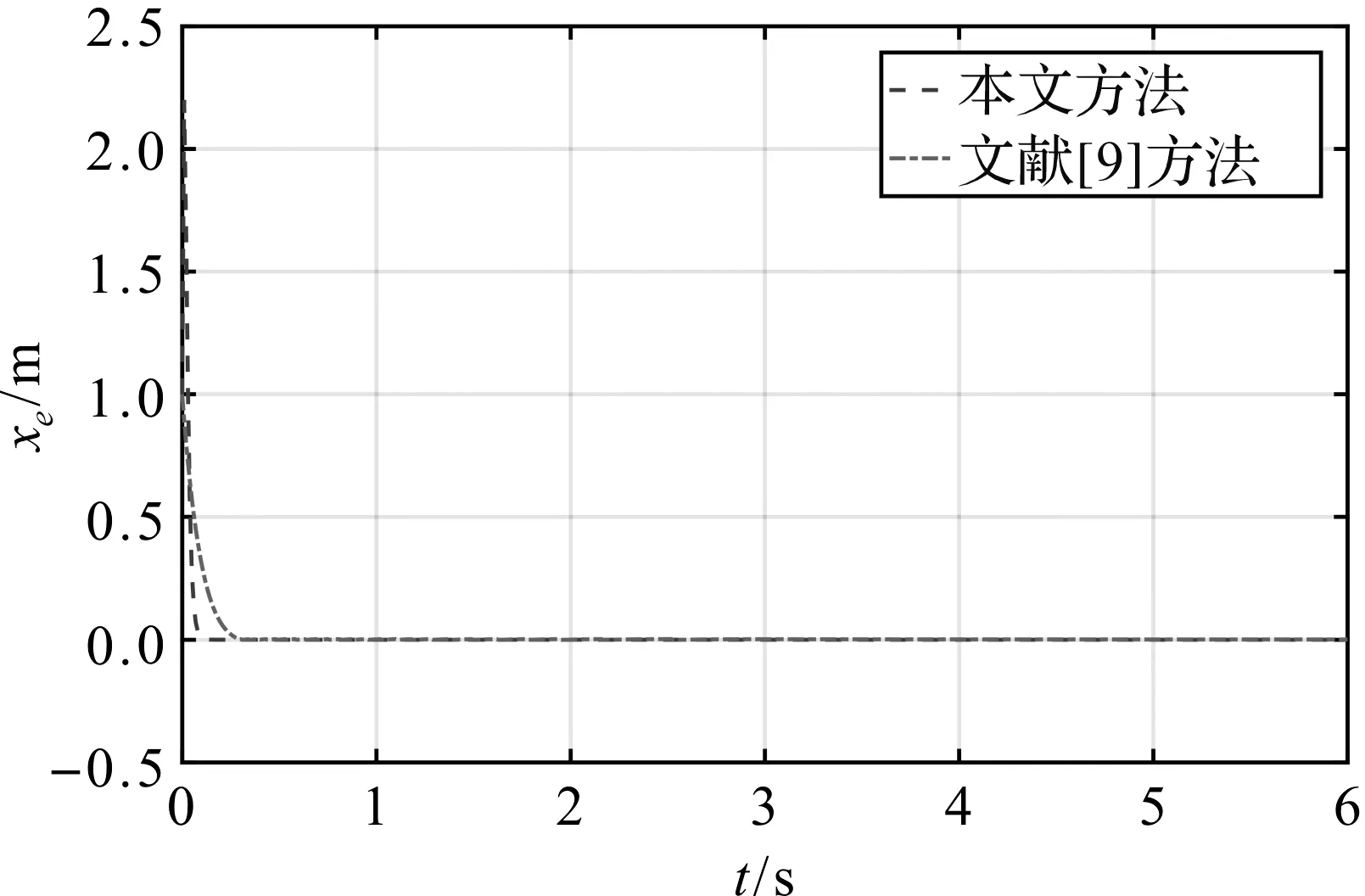
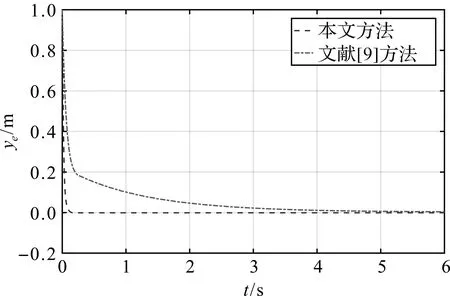
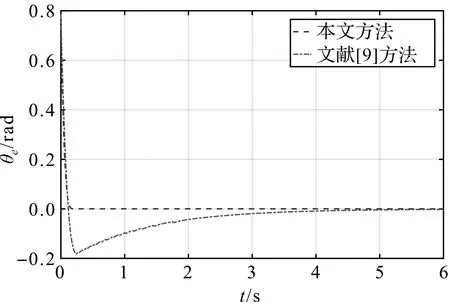
系统从s1=1到滑模面阶段，由于|s1|<1，0

(17)

由式(17)可得：

(18)

两边移项求定积分，得：

(19)

由式(19)解得系统从s1=1到达滑模面阶段的时间为：

(20)

由于忽略了系统中趋近律的第二项，故滑模面s1=θe在第二阶段的实际收敛时间小于t2。

因此s1从初始状态到滑模面的收敛时间不大于

ts1=t2+t1

(21)

当初始状态s1(0)<-1时，系统收敛到滑模面的时间同样分为2个阶段：从初始状态到s1=-1和从s1=-1到滑模面，分析与计算原理与系统初始状态s1(0)>1相同。

同理可证滑模面s2=k1xe-k2ωrye在有限时间内趋于0，并记s2收敛时间为ts2。

当时间t>ts1+ts2时，s1，s2收敛到0，此时

(22)

此时式(4)可简化为：

(23)

取Lyapunov函数

(24)

求导可得：

(25)

所以，当ωr≠0且为常数时，xe渐近收敛到0。由式(6)可得：

(26)

由于xe渐近收敛到0，滑模面s2，s1均已证明在有限时间内收敛到0，因此ye也渐近收敛到0。综上可知：系统在基于双幂次趋近律的滑模控制器作用下，轨迹跟踪误差xe，ye渐近收敛到0，θe在有限时间内收敛到0。

3 仿真结果及分析

为了验证本文设计的控制律的有效性，通过MATLAB软件对轨迹误差收敛性和参考轨迹跟踪性能进行仿真。选取参考速度νr=2.6 m/s，参考角速度ωr=0.4 rad/s。给定跟踪机器人初始位姿为[2.7 1.0 -1.0]T，参考轨迹初始位姿为[2.0 1.0 2.0]T，d=0.25 m。分别选取参数α11=9，α12=0.3，α21=9，α22=0.2，p11=9，p12=9，p21=9，p22=9，q11=11，q12=5，q21=13，q22=5，k1=0.19，k2=16。仿真结果如图2—4所示。

图2 轨迹跟踪误差曲线

由图2可以看出：轨迹跟踪误差能够在0.5 s内收敛到0；图3为控制速度的变化图，图4为实际轨迹与参考轨迹的对比图，可以看出：移动机器人在双幂次趋近律滑模轨迹跟踪控制器ν和ω的作用下，机器人能够很好地跟踪参考轨迹。

图3 趋近律输出变量变化曲线

图4 圆形参考轨迹跟踪曲线

为了进一步验证本文设计的控制律的有效性，采用本文设计的控制器与文献[9]方法进行对比，本文控制器的参数同上。选取与文献[9]相同的参考速度νr=1 m/s、参考角速度ωr=1 rad/s、机器人初始位姿[0 0 0]T和参考轨迹初始位姿[1 1 π/4]T。系统轨迹跟踪误差xe，ye，θe仿真对比结果如图5—7所示。

图5 xe误差曲线对比图

图6 ye误差曲线对比图

图7 θe误差曲线对比图

由图5—7可以看出：本文设计的双幂次趋近律滑模控制器控制的轨迹跟踪误差xe，ye，θe收敛速度明显快于文献[9]，说明本文设计的控制系统具有良好的轨迹跟踪性能。综上可知，系统对不同参考速度和角速度进行轨迹跟踪，移动机器人轨迹跟踪误差能较快收敛到0。

4 结束语

本文研究了轮式移动机器人的轨迹跟踪问题，提出一种基于双幂次趋近律的快速滑模轨迹跟踪控制方案。在机器人质心与几何中心不重合的情况下，采用双幂次趋近律设计滑模控制器，保证系统轨迹跟踪误差快速收敛到0，提高了系统的跟踪性能。但是，本文只考虑轮式移动机器人的角速度不为0的情况，下一步将针对角速度为0的情况展开进一步研究。