极大Schrödinger算子的一个加权不等式
蔡 吟,张纯洁,2
(1.杭州电子科技大学理学院,浙江 杭州 310018;2.浙江大学出版社期刊分社,浙江 杭州 310007)
0 引 言
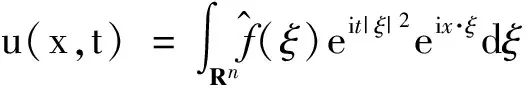
在高维欧式空间上,首先由P.Sjölin[3]和L.Vega[4]分别证明:当s>1/2时,对任意n,极限均成立。更精确的结果由S.Lee[5]和J.Bourgain[6]给出:当s>1/2-1/4n时,对任意n≥2,极限均成立,其中,n=2时的结果由文献[5]用双线性限制法得到,n≥3的结果由文献[6]用多线性法得到。
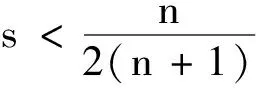
1 主要命题及证明
命题的证明需要用到以下引理:
引理[11]设g∈L2(Sn-1),则当a>1时,
定理1当a≥2时,
(1)
当a>1,α>1/2时,
(2)
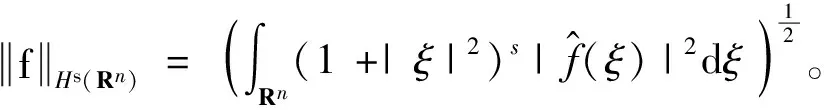
证明利用极坐标变换及变量替换,
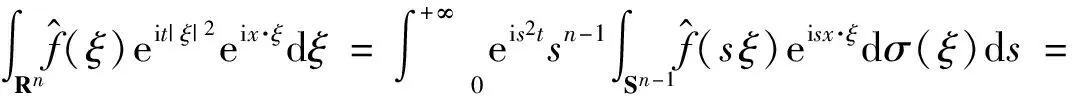
其中,i为虚部单位。由Fourier逆变换公式,
利用Plancherel定理,有
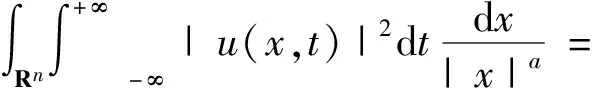
(3)
注意到f∈Hs(Rn),从而根据引理可知,式(3)不超过
(4)
最后再作变量替换及极坐标变换,式(4)不大于
因此当a≥2时,
再利用Plancherel定理,有
再用相同的方法化简得到:
注意到,a>1,α>1/2,因此
证毕。
利用定理1结论可得到定理2:极大Schrödinger算子的有界性。
定理2当b≥2时,对任意s≥1/2,有
其中,u*(x)=supt|u(x,t)|。
证明首先,利用式(1)在a=2时的结论,对于任意b≥2,有:
另外对任意b≥2,选取合适的正整数p,q,借助对应均值不等式
并取α充分靠近1/2,使之满足1 因此,当u(x,t)∈Hα(R)时,借助Plancherel定理,可得: 证毕。 最后再用极大函数法,即可获得u(x,t)(t→0)在f∈Hs(Rn),s>1/2上的逐点收敛性。 Schrödinger方程是调和分析中的一个重要内容,关于其逐点收敛到初值问题的解的研究有很多。本文主要是针对文献[11]中指出文献[4]中的证明细节问题,利用极大Schrödinger算子的加权不等式,对文献[4]的证明做了适当的修正。从证明过程可以看出:修正之后,Schrödinger方程的逐点收敛性依然成立。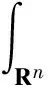
2 结束语

