任意多边形上基于ADMM的最小二乘坐标

范侠丽，王伟娜，邓重阳，李亚娟

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

重心坐标是计算机图形学和数学领域的一个重要研究方向，由A.F.Mobius于1827年首次提出，应用于图像和几何处理以及其他相关领域，如网格参数化[1]、网格变形[2]、形状变形[3]和合成[4]等。近年来，众多学者提出了许多不同的重心坐标构造方法。E.L.Wachspress[5]在广义有限元方法的背景下，提出一种有理重心坐标函数的构造方法，在凸多边形上，有效计算Wachspress坐标，但在任意简单多边形上并没有明确的定义。M.S.Floater[6]在网格参数化的背景下，提出均值坐标，在任意简单多边形上都有明确的定义，但在凹多边形内部的部分点会产生负均值坐标，不满足非负性。随后，为了使得到的坐标满足非负性，基于优化方法的重心坐标得到了很大的发展。P.Joshi等[7]基于带有特定边界条件的Laplace方程的标准有限元离散化方法，提出了调和坐标。Zhang J.Y.等[8]基于最小化全变差模型，提出了局部重心坐标。相对于调和坐标，局部坐标具有更好的局部支撑性。调和坐标和局部重心坐标虽然能够很好地保证非负性，但均涉及到区域的三角剖分，不同的三角剖分结果往往会产生不同的重心坐标[9]。为了克服上述局限性，本文提出一种适用于任意简单多边形的广义重心坐标，通过最小化基于2正则化模型的最小二乘目标函数来计算，得到的坐标是非负的、光滑的。更重要的是，本文提出的最小二乘坐标不依赖于三角剖分。

1 最小二乘坐标

设Ω⊂R2是一个以v1,v2,…,vn,n≥3为顶点的多边形。若对任意v∈Ω，存在函数λi:Ω→R,i=1,…,n满足

(3)非负性：λi(v)≥0。

则称λi(v)为定义在Ω上的广义重心坐标。

此外，为了保证插值的效果和实际应用的需要，坐标函数λi还需要具备以下性质：

(2)线性：λi(v)在边上是线性的；

(3)光滑性：λi(v)在Ω上平滑变化。

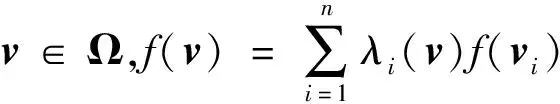
在以上性质中，非负性保证插值函数可表示为原始数据的凸组合，从而避免出现与拖曳方向反方向的变形；拉格朗日性和线性保证插值函数有效地插值边界；坐标的光滑性保证了插值效果的光滑性。

1.1 模型提出

令vi,i=1,…,n为n边多边形的顶点，v为多边形内部任意一点。对所有的坐标函数而言，最小化2-范数的和，并且该坐标函数满足线性重构性、单位性、非负性：

(1)

1.2 角平分线法

为了使求得的坐标满足拉格朗日性和线性，首先对多边形的顶点vi,i=1,…,n作一系列的线性变化，这个变换方法称为角平分线法。

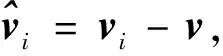
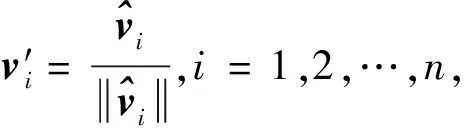
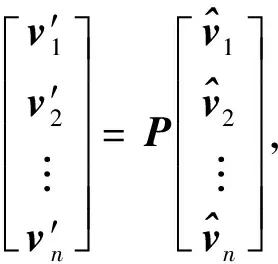
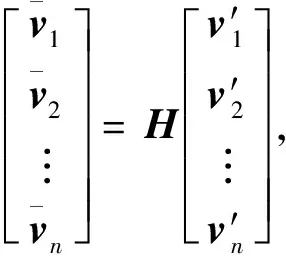
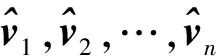
由于对式(1)中的顶点vi进行了一系列的线性变换，故与式(1)等价的模型如下：

满足：

(2)

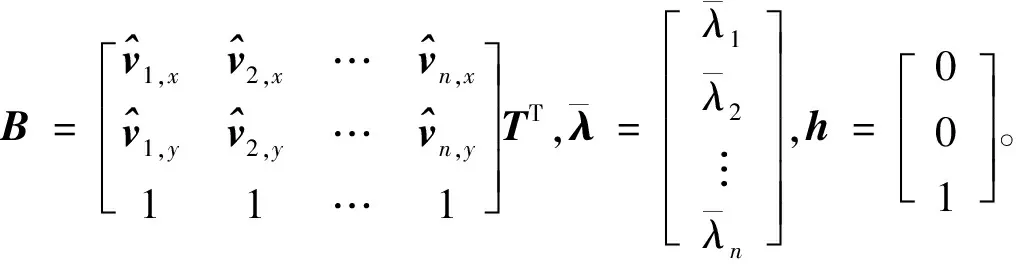
由于模型(2)是一个带有线性约束和不等式约束的凸优化问题，可以使用ADMM算法去求解。

在此，引入辅助变量y和声明变量δ(yi)：

所以，模型(2)等价于

满足：

(3)

1.3 模型实现

由于模型(3)具有可分离的目标函数和线性约束，而ADMM算法可用于处理带有线性和不等式约束的凸问题，所以，用ADMM算法进行求解。对于模型(3)，定义下面的增广拉格朗日函数：

(4)

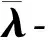
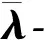
(5)

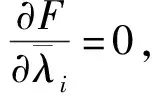
等价于

(6)

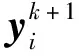
(7)

给出。

2 实验和分析

一般情况下，局部重心坐标需要对区域进行三角剖分，使得三角剖分顶点包括域内部的采样点以及所有的控制顶点。计算调和坐标也需要对区域构造一个密集的三角剖分。与局部重心坐标和调和坐标不同，本文提出的最小二乘坐标不需要对区域进行三角化，这使得对重心坐标的求解更加容易。另一方面，最小二乘坐标是非负的，保证了重心插值的凸包性。

最小二乘坐标、均值坐标、调和坐标在凸、凹顶点坐标函数的比较如图1、图2所示。从图1、图2可以看出：图1凸顶点的均值坐标在L型多边形的灰色区域内为负值，最小二乘坐标和调和坐标一样，是非负且光滑的。另外，在计算时间方面，调和坐标的运行效率相对较快，但它需要预先进行三角剖分，所以其结果受到不同剖分方法的影响；而最小二乘坐标不需要进行剖分，结果比较稳定。

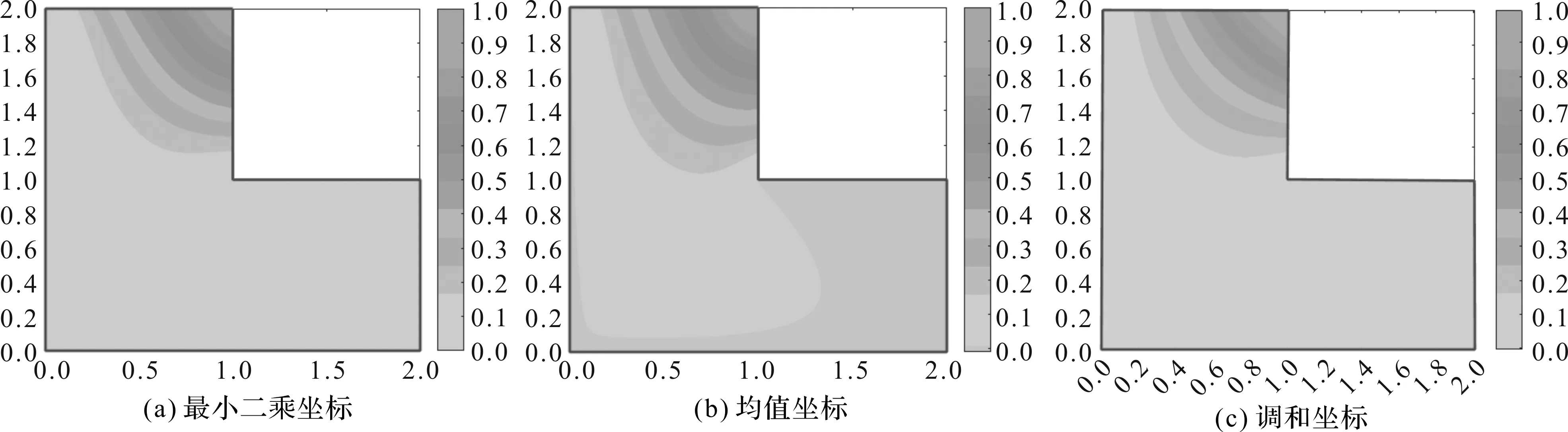
图1 L型多边形凸顶点的重心坐标

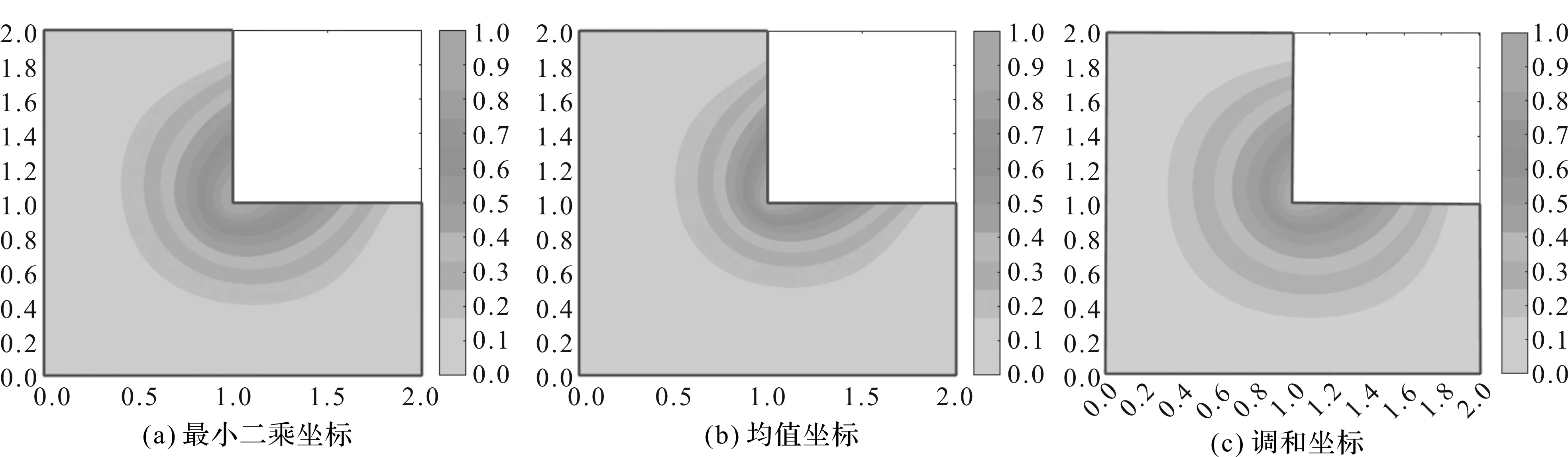
图2 L型多边形凹顶点的重心坐标

图3、图4进一步展示了在十边形、十三边形上所得到的最小二乘坐标例子。从图中可以看出，最小二乘坐标满足非负性、光滑性、拉格朗日性、线性等性质。图5展示了在图像变形中，通过改变多边形的顶点坐标来实现最小二乘坐标变换的应用实例。图5中，4个黑色实心点为四边形的控制顶点，通过改变四边形顶点的位置，来实现花朵的变形。

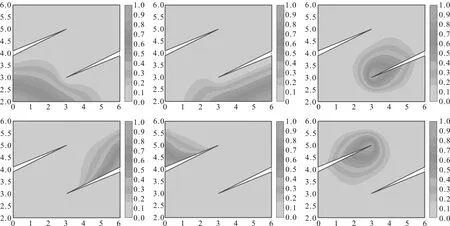
图3 十边形中个别顶点的最小二乘坐标实例

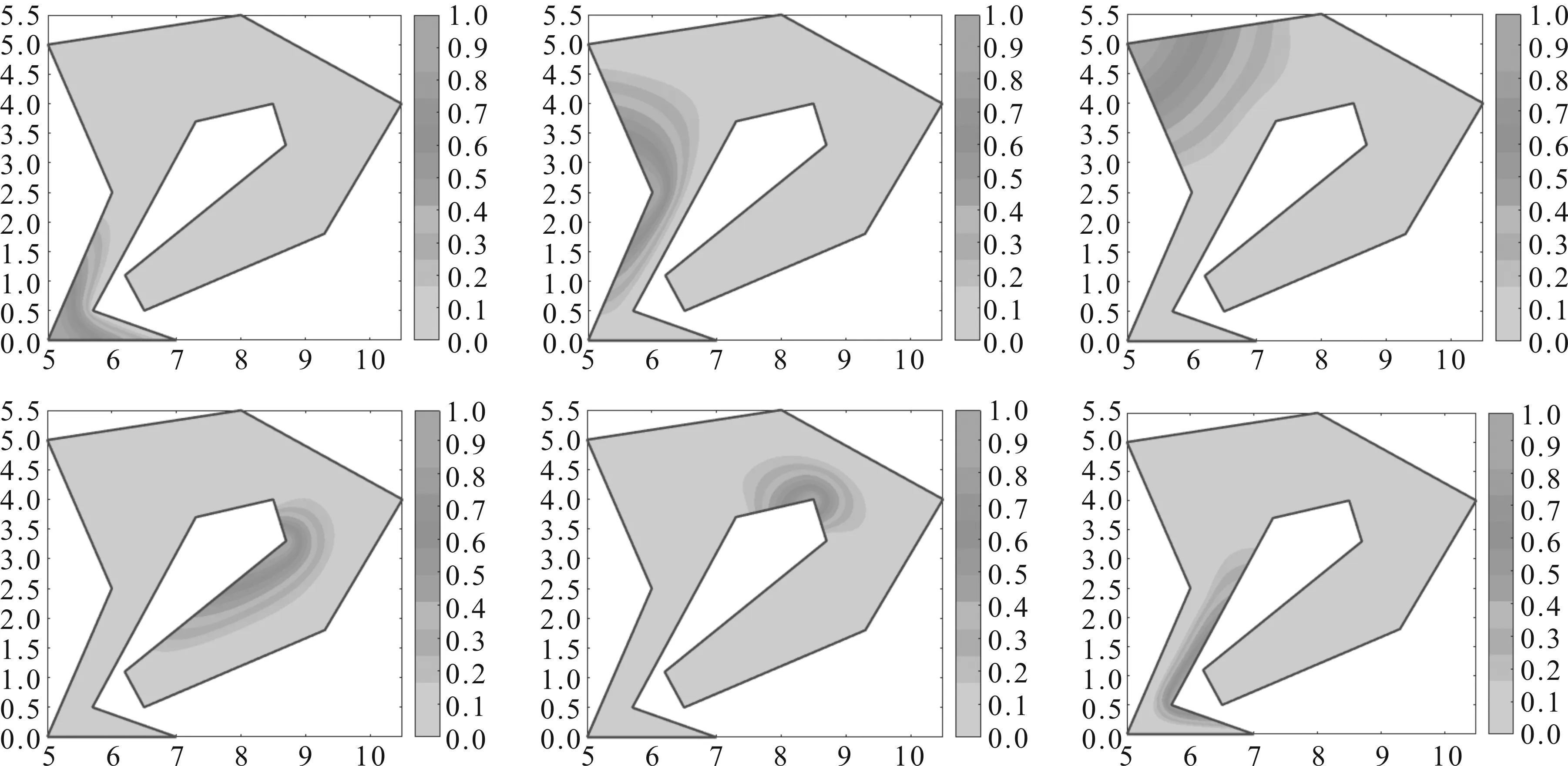
图4 十三边形中个别顶点的最小二乘坐标实例

图5 最小二乘坐标的图像变形

3 结束语