二维指数差分方程的全局动力学行为分析

张千宏，林府标，李东阳，张钟妮

(贵州财经大学 数统学院，贵州 贵阳 550025)

众所周知，差分方程以离散模型的形式出现，作为微分方程和时滞微分方程的数值解，在经济学、生物学、计算机科学、控制工程等领域有着广泛的应用，因此，它已成为应用数学中的一个重要课题和热点问题.特别地，由于理论或应用的重要性，差分方程(系统)的动力学问题已被许多学者所研究.

EI-Metwally等[1]研究了离散人口模型xn+1=α+βxn-1e-xn,n=0,1,2,…的全局稳定性,其中α>0表示移民率，β>0表示人口增长率,初值x-1,x0为正实数.

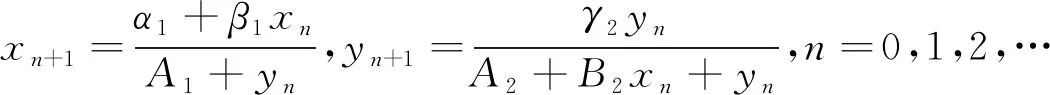
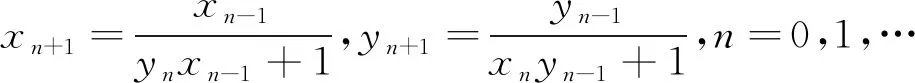
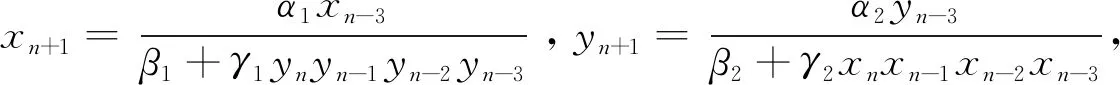
基于上述讨论，进一步研究如下差分方程系统

(1)

的有界性、持久性、稳定性和渐近性, 其中αi，βi，γi∈(0，∞),i=1,2,初值xi,yi∈(0,∞),i=-1,0.

1 预备知识

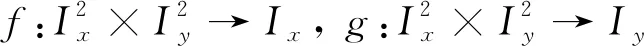
(2)

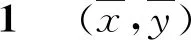
定义2设Ix,Iy是实数区间，Ix×Iy被称作方程(2)的不变集，如果当n>0，x0,x-1∈Ix,y0,y-1∈Iy⟹xn∈Ix,yn∈Iy.

定义3(xn,yn)是持续有界的，如果存在正数M,N,使得

M≤xn≤N,M≤yn≤N,n=-1,0,….

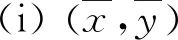
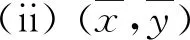
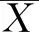
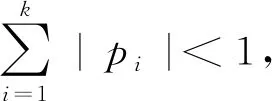
xn+k+p1xn+k-1+p2xn+k-2+…+pkxn=0,n=0,1,…

是渐近稳定的.

2 主要结论

2.1 有界性和持续性

定理3系统(1)每个正解都是有界和持久的.

证明如果(xn,yn)是(1)的一个任意解，则

(3)

由(1)，(3)式，有

(4)

由(3)，(4)式得 ，当n≥3时，有

2.2 不变集的存在性

定理4如果(xn,yn)是(1)的一个任意解，则集合

是系统(1)的不变集.

证明设系统(1)的正解(xn,yn)满足初值

由(1)式,有

且

因此

令n=m，假设

由(1)式可得

定理4证毕.

2.3 正平衡点的存在性和唯一性

定理5如果

(5)

证明考虑系统

(6)

系统(6)可以表达成如下形式

(7)

F(y)=y2+γ2y-α2-β2e-h(y)，

(8)

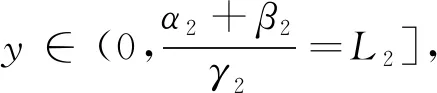
所以至少存在一个正解y∈(0,L2].

另一方面，由(5)，(7)式，有

F′(y)=2y+γ2+β2e-h(y)h′(y)=

(9)

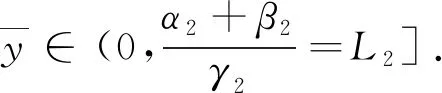
定理5证毕.

2.4 正平衡点的稳定性

定理6考虑差分方程系统(1)，下列结论成立：

(i) 如果

(10)

(ii) 如果

(11)

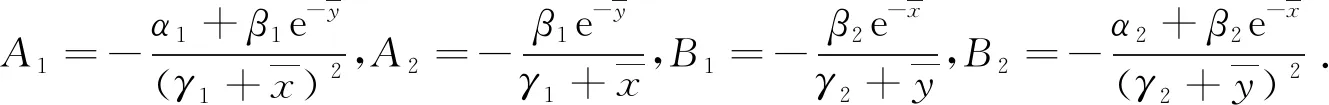
λ4-(A1+B2+A2B1)λ2+A1B2=0,

(12)

则

(ii) 类似地，可得

定理7如果

(13)

证明考虑

因为当∀x>0时，-1+x-lnx≥0，从而Gn>0.

(14)

由(13)，(14)式，得

(15)

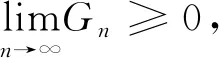
3 数值例子

下面给出一个例子来验证所得理论结果的有效性.

例子考虑系统(1).如果α1=48,β1=4,γ1=13,α2=68,β2=5,γ2=14，初值x-1=12,x0=10，y-1=8,y0=4,此时系统(1)可以写成如下形式

(16)

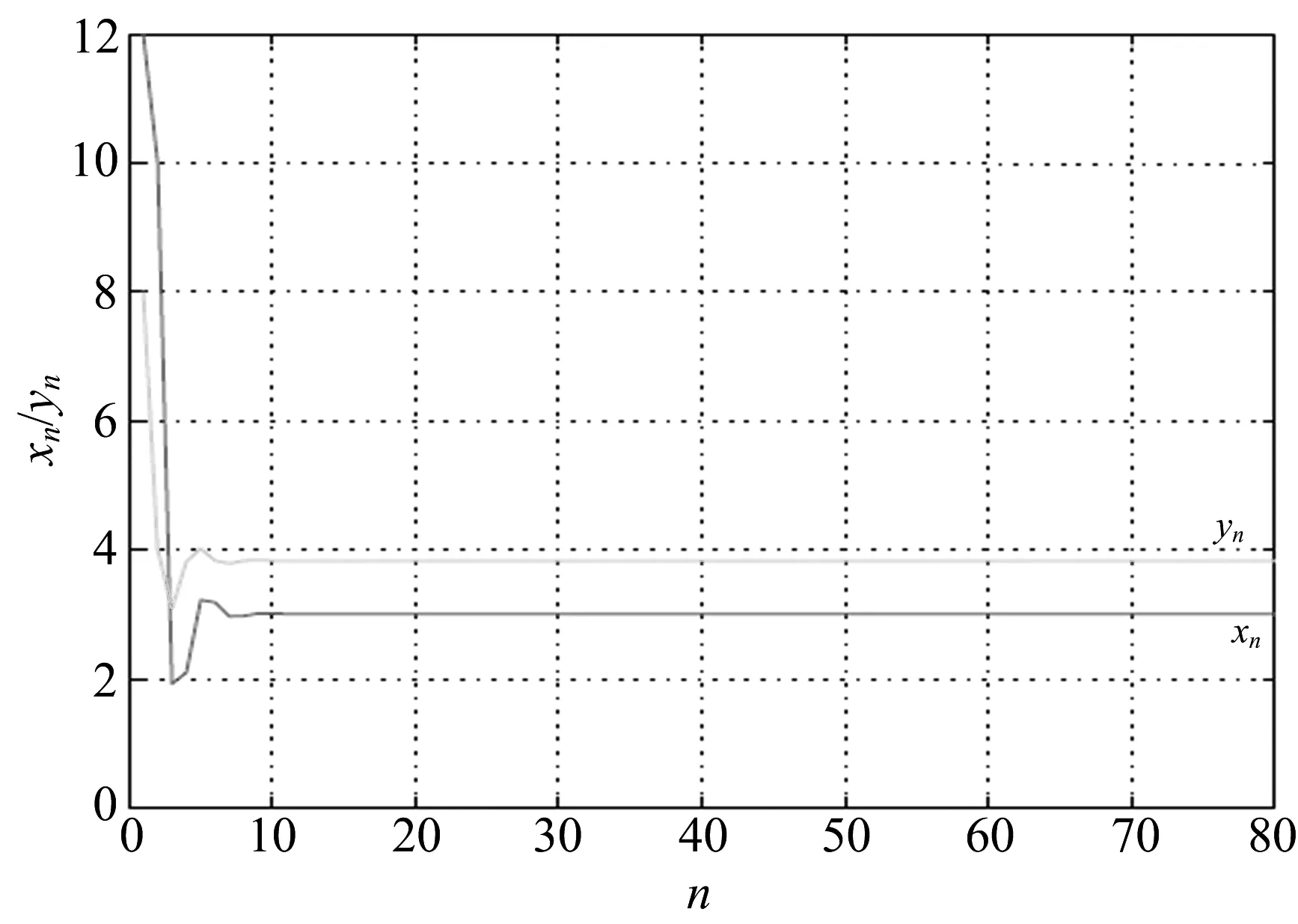
图1 系统(16)的动力学行为

4 结束语

论文研究二维指数型差分方程系统的动力学行为, 所得主要结论如下：

(1) 系统(1)的每个正解都是有界持续的.

(2) 系统(1)的不变集为