群作用下逆极限空间中移位映射的动力学性质

冀占江，覃桂茳*，张更容

(1.梧州学院 大数据与软件工程学院，广西 梧州 543002;2.梧州学院 广西高校图像处理与智能信息系统重点实验室，广西 梧州 543002;3.湖南第一师范学院 数学与计算科学学院,湖南 长沙 410205)

1 基本定义

定义1设X，Y是度量空间，称f是一个同胚映射，如果f:X→Y是一个一一映射，并且f，f-1都是连续的．

定义2设X是度量空间，A⊂X，f:X→X连续，若f(A)⊂A，则称A对f不变.

定义3设X是度量空间，A⊂X，f:X→X连续，若f(A)=A，则称A对f强不变.

定义4[13]设X是度量空间，G是拓扑群．若映射φ:G×X→X满足：

(1) 对任意的x∈X，有φ(e,x)=x，其中e为G的单位元；

(2) 对任意的x∈X以及g1，g2∈G，有φ(g1,φ(g2,x))=φ(g1g2,x)，则称(X,G,φ)是度量G-空间，简称X是度量G-空间．为书写方便，通常将φ(g,x)简写为gx．特别地，若X是紧致度量空间，则称X是紧致度量G-空间．

定义5[14]设X，Y是度量G-空间，f:X→Y连续，称f是等价映射，如果∀g∈G，∀x∈X，有f(gx)=gf(x)．

定义6[15]设X，Y是度量G-空间，f:X→Y连续，称f伪等价映射，如果∀g∈G，∀x∈X，∃h∈G，有f(gx)=hf(x)．

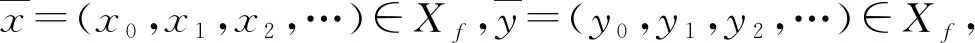
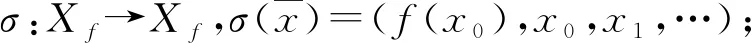
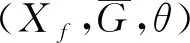
定义9[16]设(X,d)是度量G-空间，f:X→X连续，x∈X，称x是f的G-周期点，如果存在n∈N+，∃g∈G，使得gfn(x)=x，满足gfn(x)=x的最小正整数称为x的G-周期．f的G-周期点集用PG(f)表示.

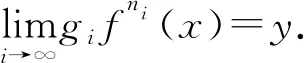
定义11[17-18]设(X,d)是度量空间，f:X→X连续，x∈X，称x是f的回归点，如果对任意x的领域U，存在n∈N+，使得fn(x)∈U.f的回归点集用R(f)表示．

定义12设(X,d)是度量G-空间，f:X→X连续，x∈X，称x是f的G-回归点，如果对任意x的领域U，存在n∈N+，∃g∈G，使得gfn(x)∈U.f的G-回归点集用RG(f)表示．

2 若干引理

引理1设X，Y是度量G-空间，f:X→Y伪等价(等价)，则：

(1) ∀m≥2，fm伪等价(等价)；

(2) 若f:X→Y同胚，则f-m:Y→X伪等价(等价)，m≥1.

证明(1)由f伪等价,知∀x∈X，∀g∈G，∃h∈G，有f(gx)=hf(x)，故f2(gx)=f(hf(x)).同样由f伪等价,知∃t∈G，使得f(hf(x))=tf2(x)，故f2(gx)=tf2(x)，因此f2伪等价．以此类推可得fm伪等价．

(2) ∀x∈X，∀g∈G，由f同胚，知存在唯一点y∈X，使得f(y)=x，故f-1(gx)=f-1(gf(y)).由f伪等价，知∃t∈G，使得f-1(gf(y))=f-1f(ty)=ty，故f-1(gx)=tf-1(x)，因此f-1:Y→X伪等价．以此类推可得f-m伪等价．

引理2设(X,d)是度量G-空间，f:X→X伪等价映射，则f(PG(f))⊂PG(f).

证明设y∈PG(f)，则∃m∈N+，∃g∈G，使得gfm(y)=y．由f是伪等价，可知∃h∈G，使得hfm(f(y))=f(y)，故f(y)∈PG(f)，因此f(PG(f))⊂PG(f)．

注1由于PG(f)对f不变，因此可以考虑f在PG(f)上形成的逆极限空间，后面的定理1给出了具体的结论.

引理3设(X,d)是度量G-空间，f:X→X同胚等价，x∈X，则wG(x,f)是闭集，且f(wG(x,f))=wG(x,f).

证明wG(x,f)是闭集和f(wG(x,f))⊂wG(x,f)的证明见文献[16].下面证明wG(x,f)⊂f(wG(x,f)).

设z∈wG(x,f)，则∃{nk}⊂N+，∃{gk}⊂G，使得gkfnk(x)→z,k→∞. 又f同胚等价，由引理1的(2)，知f-1等价，因此gkfnk-1(x)→f-1(z),k→∞，故f-1(z)∈wG(x,f)，则wG(x,f)⊂f(wG(x,f)).

引理4设(X,d)是度量G-空间，f:X→X同胚等价，则WG(f)是闭集，且f(WG(f))=WG(f).

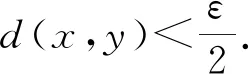
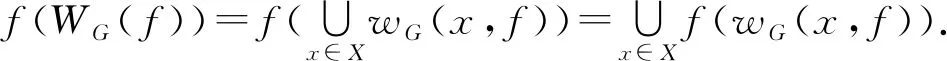
注由于WG(f)对f强不变，因此可以考虑f在WG(f)上形成的逆极限空间，后面的定理2给出了具体的结论.

引理5设(X,d)是度量G-空间，f:X→X连续，x∈X，则∀i∈N+，有wG(fi(x),f)=wG(x,f).

证明先证wG(fi(x),f)⊂wG(x,f).设y∈wG(fi(x),f)，则∃{gk}⊂G，∃{nk}⊂N+，使得gkfnk(fi(x))→y,k→∞，即gkfnk+i(x)→y，故y∈wG(x,f).

下证wG(x,f)⊂wG(fi(x),f). 设t∈wG(x,f)，则∃{pk}⊂G，∃{mk}⊂N+，使得

pkfmk(x)→t，

即pkfmk-i(fi(x))→t，故t∈wG(fi(x),f)，则wG(fi(x),f)=wG(x,f).

引理6设(X,d)是度量G-空间，f:X→X伪等价，则f(RG(f))⊂RG(f).

证明设x∈RG(f)，则x∈wG(x,f).由引理3，知f(wG(x,f))⊂wG(x,f)，故f(x)∈wG(x,f).由引理5，知wG(f(x),f)=wG(x,f)，则f(x)∈wG(f(x),f)，故f(x)∈RG(f)，因此f(RG(f))⊂RG(f).

注2由于RG(f)对f不变，因此可以考虑f在RG(f)上形成的逆极限空间，后面的定理3给出了具体的结论.

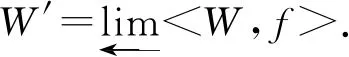
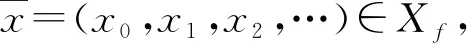
3 主要定理

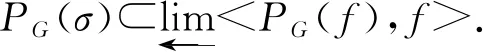
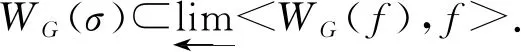
故

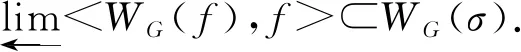
f(wG(yi,f))=wG(yi,f).