基于自适应阻抗控制的轮足式机器人隔振控制研究

汪首坤，史明新，岳斌凯，徐康，王军政

(北京理工大学 自动化学院，北京 100081)

机器人隔振力控制是机器人运动控制中的一个关键环节[1-3]. 在机器人与环境发生相互作用时，其轨迹受到环境的限制，如果不施加相应的控制策略应对这一情况的话，环境将会对机器人控制产生严重的影响[4]. 本文的研究对象4腿轮足式机器人在以轮式运动经过坑洼路面时，机身会产生剧烈的起伏，对机器人整体控制不利，甚至发生翻车事故,因此在其运动过程中需要对其施加隔振控制.

机器人隔振力控制可以分为两种类型：主动隔振与被动隔振[5]. 被动隔振通常在机器人末端安装一个弹簧-阻尼的装置作为吸能缓冲元件，对高频振动的隔振效果较好. 但对于低频振动则需要施加主动隔振策略来进行抑制，国内外众多学者针对主动隔振策略进行了大量的研究.

在Hogan[6]提出阻抗控制模型之后，阻抗控制在机器人隔振柔顺力控制领域得到广泛的应用. 阻抗控制通过一个目标阻抗模型将环境力与机器人位置建立起一个动态的关系，从而间接控制这两个量. 其中基于位置的阻抗控制是建立在位置闭环的基础上，因此不需要知道受控系统精确的数学模型，算法简单易实现，因此被广泛的应用. 但该方法也存在明显的缺点，阻抗模型的参数估计反映着对环境的认识情况，想要达到良好的控制效果，需要对环境模型有较为准确的估计. 但实际中，外界环境常常是未知或者多变的，对环境参数估计的较小误差，由于环境刚度通常极大，因此将造成极大的力误差. 传统的阻抗控制因为存在阻抗参数固定不变的弊端，因此对于多变环境的适应性较差. 为改善这一缺点，众多学者做了很多相关工作. Kang等[7]分析了阻抗控制中存在的建模误差对阻抗控制精度和鲁棒性影响较大的问题，提出了一种基于内部模型控制结构与延时估计的方法，可以动态校正系统建模误差，提高力控精度. Love等[8]对阻抗控制器的动态特性进行分析，提出一种对任意环境都可以进行辨识的方法，当机器人从非约束状态向受约束状态转换时，能够对控制结构进行修正使过渡过程更加平稳. Xiao等[9]提出基于多传感器融合控制策略，结合加速度反馈设计控制器，一定程度上解决了机器人末端对环境的准确跟踪问题.

本文在基于Lyapunov第二稳定定理的基础上设计了一种自适应阻抗控制器，通过一个位置补偿量达到了间接调整阻抗参数的目的，提升了控制算法对多变环境的适应性. 通过设计Lyapunov能量函数，得到自适应补偿函数的表达式. 在系统稳定的前提下，实现了系统稳态误差为0的目的. 然后针对机器人轮式运动通过不同减速带的隔振问题进行了仿真与实验，证实了该方法的有效性.

1 阻抗控制

1.1 阻抗控制原理

阻抗控制的核心思想是将机器人等同于物理系统，环境等同于导纳，将与环境接触执行相应操作的部分等同于阻抗. 在Hogan提出阻抗控制模型后，一般情况下，采用二阶线性方程描述一个质量-弹簧-阻尼系统来表述期望的阻抗关系

(1)

(2)

式中：E=Fe-Fr，E为力误差；Fr为期望的力. 对式(2)做拉普拉斯变换，得到期望阻抗方程在频域的表现形式

(3)

1.2 稳态误差分析

在阻抗控制中，众多学者一般将其中的环境模型简化为一个线性弹簧系统，可以将其表示为如下形式

fe=ke(x-xe).

(4)

当机器人与环境发生接触时，此时满足x≥xe，则此时的机器人位置可以表示为

x=fe/ke+xe.

(5)

(6)

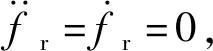
(7)

由上式发现，若想让系统的稳态力误差为0，则期望的位置需要满足如下条件

xd=fr/ke+xe.

(8)

但在实际情况中，系统的期望的位置是根据机器人的足端规划的轨迹设定的，环境的位置xd和刚度kd也是无法预知的，只能进行估计. 同时机器人运动时与外界接触的环境也可能不是一成不变的，所以xd与kd是时变的参数，这样式(8)中的条件基本是不可能被满足的. 同时，机器人与环境接触时的碰撞刚度较大，微小的估计误差会对力控制的精度造成极大的影响，因此传统的阻抗控制是难以实现精准的力控制的.

2 自适应阻抗控制

本文中使用的自适应阻抗控制的基本原理是调整目标阻抗参数去减小目标阻抗模型与理想模型之间的偏差，但并不是直接去修改阻抗控制器中阻抗参数，而是通过一个位置补偿器，用环境信息作为输入，得到一个位置的补偿量Δx，作为内位置闭环输入的一部分，因此是一种间接调整阻抗参数的方法[10]，其控制框图如图1所示.

加入位置补偿量的机器人参考输入量可以表示为

xr=xf+Δx.

(9)

机器人与外界环境发生交互时，机器人能够采集到的最直接与环境交互量为环境的反馈力，因此将Δx取为环境力与期望力的偏差及其导数与一时变量的线性组合，表现形式如下

(10)

式中：e(t)为垂直方向受力与期望力的偏差；g(t)为一时变辅助函数；p(t)与d(t)为时变系数.

将环境模型考虑为单纯弹簧模型，则将式(9)与(10)带入到基于位置的阻抗模型的误差方程(6)中，可以得到新的力误差方程为

(11)

式中：ap(t)，bp(t)，wp(t)的表达式为

(12)

(13)

式中：ap(t)，bp(t)与wp(t)都是与式(10)中的g(t)，p(t)，d(t)直接相关的，因此找到ap(t)，bp(t)与wp(t)的调整规律就可以得到位置修正量的表达式. 自适应阻抗控制器的目的是使得跟踪力误差为0，因此选取一个跟踪误差为0的理想模型，其表达式如下

(14)

同理，该表达式也可以写成状态空间的形式

(15)

(16)

在理想的情况下，利用构造的位置补偿量Δx得到的新的力误差系统是Lyapunov稳定的. 则可以先假定其为Lyapunov稳定的，从而反推出Δx的表达式. 证明力误差系统是稳定的关键是构造一个正定的Lyapunov能量函数V(Ee,t). 对于线性系统，通常使用二次型函数xTPx作为Lyapunov函数. 因此将能量函数构造为如下形式

(17)

(18)

(19)

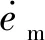
(20)

观察式(12)可以发现，ap(t)，bp(t)，wp(t)与位置修正量中的关键量d(t),p(t),g(t)的表达式之间只差一个常数和一个比例系数，因此可以得到d(t),p(t),g(t)的调整规律，如下所示

(21)

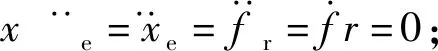
(22)

式中：μ1,μ2,μ3为小正整数；σ1,σ2,σ3为小的修正因子. 将式(22)带入到式(10)中即可得到自适应位置补偿量，至此，自适应阻抗控制器中的位置补偿量的理论推导完毕，后续进行实验验证.

3 实验与结果分析

3.1 实验系统简介

本实验的实验对象为北京理工大学自主研发的电动并联轮足式机器人，其物理样机如图2所示.

针对机器人在轮式运动模式下通过减速带的隔振问题设计实验. 实验中所要通过的减速带有高低两种，其规格分别为：高8 cm，宽80 cm；高11 cm，宽68 cm. 在机器人二号腿上施加阻抗控制. 在实验的过程中，电机的速度设定为600 r/min. 为增大扭矩在电机与轮子之间增加安装了减速比为1∶40的减速机，轮子的直径为25.4 cm，因此可以得到在理想情况下(忽略摩擦)，机器人的前进速度为0.72 km/h. 在此前提下分别采用阻抗控制与自适应阻抗控制进行实验.

衡量机器人隔振效果的好坏主要看机身加速的大小，但本实验中的加速度的频率较低，直接使用加速度传感器进行测量的话，噪声过大. 而加速度信号是与单腿受力直接相关的，因此通过比较机器人单腿受力的偏差与机器人姿态角的变化来衡量隔振控制的效果.

3.2 隔振实验研究

① 电机转速为600 r/min，机器人通过低减速带，实验结果单腿受力偏差如图3所示，机身姿态角变化如图4所示.

从图中可以看出，在不施加主动隔振力的时候，力偏差的峰值达到了908 N左右，机身的俯仰角峰值达到了7.9°. 施加主动隔振后，在通过减速带最高点前后的力的峰值均大幅度的降低. 单独阻抗控制作用时，力偏差的峰值为235 N左右，机身的俯仰角峰值为2.6°左右，施加自适应阻抗控制之后，力偏差的峰值为188 N左右，机身俯仰角峰值为2.26°左右. 由此结果可以看出加入主动隔振力控制之后，机身通过减速带的振动得到了明显的抑制. 单独施加阻抗控制时，力偏差降低了74.1%，机身俯仰角降低了67.1%；施加自适应阻抗控制后，单腿受力偏差与机身俯仰角的变化相对于纯阻抗控制有了进一步的降低. 力偏差降低了79.3%，机身俯仰角降低了71.4%，证明了自适应阻抗控制的隔振效果更优.

② 电机转速为600 r/min，机器人通过高减速带，实验结果单腿受力偏差如图5所示，机身姿态角变化如图6所示.

由于机器人在通过高减速带的时候，在不施加主动隔振力控制时，机器人是无法通过减速带的，因此无法得到不控制时，机器人单腿受力的偏差. 但通过高低减速带的高度比与姿态传感器的安装位置，可以估算出机器人在不施加隔振控制时，其俯仰角的峰值为10.3°.

从图中可以看出，机器人在通过高减速带的时候，力偏差与姿态角的变化与低减速带基本一致. 单独施加阻抗控制时，力偏差的峰值为417.8 N左右，机身的俯仰角峰值降低至2.95°左右，施加自适应阻抗控制之后，力偏差的峰值降低为284.5 N左右，机身俯仰角峰值降低至2.6°左右. 由此结果可以看出加入主动隔振力控制之后，机身通过减速带的振动得到了明显的抑制. 单独施加阻抗控制时，机身俯仰角降低了71.4%；施加自适应阻抗控制后，单腿受力偏差与机身俯仰角的变化相对于纯阻抗控制有了进一步的降低，尤其是经过减速带最高点之后的力偏差降低更多. 机身俯仰角降低了74.8%，力偏差相比阻抗控制进一步降低了31.9%，证明了自适应阻抗控制的隔振效果更优.

4 结 论

本文提出了一种自适应阻抗控制的方法. 该算法通过增加一个位置补偿量来达到间接调整阻抗参数的目的. 使用Lyapunov第二稳定性定理，通过巧妙的设计Lyapunov能量函数，得出自适应补偿函数的表达式. 在保证系统稳定的前提下，达到稳态误差为0的目的，提高了控制算法对多变环境的适应性，弥补了阻抗控制的不足. 并针对电动并联机器人轮式运动通过减速带的隔振问题设计了实验. 实验结果证明施加主动隔振力控制后，机器人的振动得到明显的抑制，并且自适应阻抗控制相比与传统阻抗隔振效果更好.