爆破漏斗鼓包运动模型的构建及验证

张智宇，陈春超，黄永辉，李洪超，雷振，王建国,5

(1.昆明理工大学 国土资源工程学院，云南，昆明 650093； 2. 昆明理工大学 电力工程学院，云南，昆明 650500； 3. 昆明理工大学 城市学院，云南，昆明 650051;4.贵州理工学院 矿业工程学院，贵州，贵阳 550025； 5.云南农业大学 建筑工程学院,云南，昆明 650201)

爆破技术已经广泛运用于国民经济生产的各个行业中，除矿山开采外，在水利工程建设、铁路铺设和城市废旧建筑拆除中也得到了广泛的应用. 在岩土爆破过程中，应力波与爆轰气体共同作用于岩体，使岩体约束减小、阻力降低，同时爆轰气体使岩石自由面产生鼓包运动，并向四周抛掷岩体.

前人多通过爆破漏斗试验[1-3]对岩体爆破机理进行研究，李祥龙等[4]通过爆破漏斗相似模型试验指出爆炸冲击波、爆生气体、碎石间相互碰撞作用是鼓包运动产生的主要原因，并且鼓包运动为一个加速过程；时党勇[5]运用高速摄影系统对内爆条件下钢筋混凝土自由面的鼓包运动状态进行分析，结果表明应力波使岩体产生初期裂纹，爆轰气体载荷进一步推进鼓包运动的形成；李世海等[6]对水、淤泥和岩土等介质的爆炸运动规律进行分析，指出鼓包运动是高压气体膨胀和介质惯性运动共同作用的结果，同时指出岩体的强度对鼓包运动形态无影响；李祥龙等[7]采用高速摄影仪对爆破漏斗鼓包运动进行观测，指出鼓包中心经历加速-匀速-二次加速-减速等变速过程，当鼓包上升到约1.5倍抵抗线后，按弹道运动规律进行抛掷. 肖建光等[8]运用量纲分析法对抛掷爆破混凝土介质飞散行为进行研究，得到爆破后混凝土介质的平均抛掷速度；黄永辉等[9]运用矢量叠加方法对岩石的抛掷速度进行分析，并得出岩石的投掷距离.

前人多对爆破漏斗鼓包运动机理与形态进行分析，鲜有人对鼓包运动速度进行量化，本文将运用动量守恒定律对鼓包运动规律进行分析，并建立相应数学模型；采用高速摄影系统对自由面鼓包运动进行观测，同时采用数值分析方法对自由面鼓包运动速度模型进行验证，确立运动速度模型，为工程爆破提供合理、有效的安全参考依据.

1 鼓包运动理论及鼓包运动数学模型的建立

1.1 爆破漏斗鼓包运动理论

爆破漏斗作为爆破破坏的基本形式,在爆炸应力波作用阶段[10-12]，爆炸冲击波作用于炮孔壁，使其产生粉碎破坏区，并衰减成应力波；应力波沿最小抵抗线方向传播到自由面并产生反射，同时产生拉伸破坏；其他抵抗线方向上的应力波随后作用于自由面，并在裂隙尖端产生应力集中，使裂隙进一步发育. 在爆生气体作用阶段[13-14]，爆生气体作用于裂隙，使裂隙进一步发育，在最小抵抗线方向上首先出现鼓包运动，如图1所示，炮孔中心位移率先达到最大值，当鼓包运动完成时，破碎岩块沿最小抵抗线方向进行抛掷[15].

1.2 鼓包运动数学模型的建立

在半无限介质中进行爆破漏斗试验过程时，在爆生气体压力作用下，岩体以推移的运动形式向四周抛散；为研究岩体鼓包运动规律与岩体抛掷速度，在爆破漏斗试验过程中，将岩体划分成多个有限单元，如图2所示，每块岩体的受力面积相同，即具有相同的动能[16].

根据能量守恒，每一单元所具有的动能为

(1)

式中：E为每个岩体单元所具有的动能；mi为岩体单元i的质量；vi为岩体单元i的速度；m1为第1个岩体单元质量；v1为第1个岩体单元速度.

根据式(1)可得每个单元在运动过程中其运动速度为

(2)

设岩体密度均匀，v1的相对运动速度为1，根据式(2)可得其余单元体速度，见表1.

表1 岩体单元运动位移表

为获得岩体运动速度分布形态与表达式，对表1中岩体运动位移进行拟合，则可得岩体运动速度为

(3)

式中：vi为岩体单元i的运动速度；xi为自由面炮孔中心为原点的坐标距离.

为进一步分析岩体运动分布形态，绘制式(3)拟合曲线，如图3所示. 由图可知，拟合曲线服从指数分布，相关性系数为0.98，表明拟合曲线与岩体运动理论速度具有很高的拟合度. 靠近炮孔中心位置的速度率先达到最大值，并随自由面炮孔中心距离的增大而降低，鼓包运速度呈指数递减.

利用最小二乘法对鼓包运动速度建立指数数学模型，

(4)

式中：vi为岩体单元i的运动速度;xi为以自由面炮孔中心为原点的坐标距离.

当x为0时可得某一时刻鼓包中心最大抛掷速度为

vmax=ea,

(5)

则

(6)

由式(6)可知，鼓包运动速度属于典型的非线性问题，为确定爆破漏斗鼓包运动位移式(6)中未知参量a、b、c，对式(6)线性化，并建立关于未知量α、b、c的回归模型. 利用Leveneberg-Marquard方法[16]将模型(6)拟合到所得数据点：

(xi,vi)={(x1,v1),……,(xn,vn)},

(7)

找出a、b、c最小误差向量的RMSE

(8)

在n个数据点上计算r的偏导数为一个n×3的矩阵：

Leveneberg-Marquard使用初始估计(a，b，c)=(1,1,1),λ固定在50，将会得到最优的最小二乘模型

(10)

图3为爆破漏斗自由面某一具体时刻岩体运动理论速度曲线，结合指数运动速度模型对自由面鼓包运动进行分析. 在爆生气体作用过程中随着岩体进一步破裂，爆生气体压力出现变化，岩体做变速运动；由式(6)可知，某一时刻，最小抵抗线方向上岩体运动速度先达到最大值，随离炮孔中心距离的增大，岩体运动速度呈指数递减，自由面整体呈现“凸”状.

2 爆破漏斗试验方案

2.1 模型材料力学试验

相似模型试验能够在一定程度上反应原型的特征，有利于模型试验与现场试验的结合，为便于今后进一步分析岩石力学特性与鼓包运动的关系，开展相似配比试验研究，以水泥、石英砂和水为材料，按质量比1∶5∶1制作10 cm×10 cm×10 cm素混凝土模型试件，并在自然环境下养护28 d. 对标准试件进行单轴抗压(见图4)、纵波波速等物理力学性质试验研究.

对预制的9个模型试件进行静态物理力学参数测试，取其平均值作为爆破漏斗试验材料的静力学参数，如表2，以此做参考，制作爆破漏斗模型.

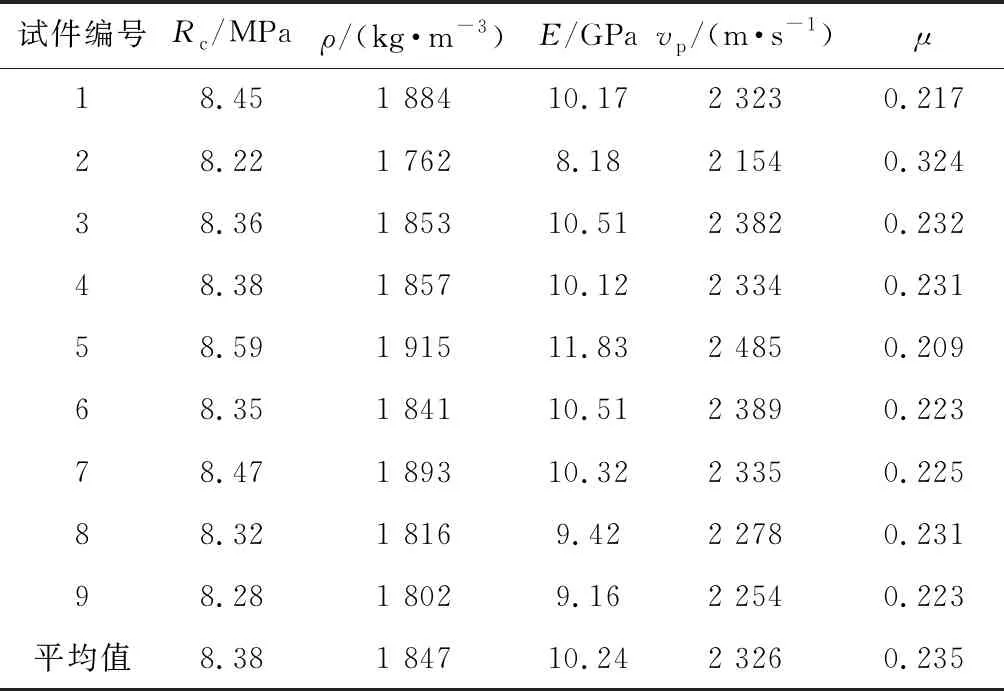
表2 基本物理力学参数

2.2 爆破方案

试验采用质量配比(m(水)∶m(水泥)∶m(砂)=1∶5∶1浇筑4个素混凝土模型，模型直径为50 cm，并用钢筋预留直径为1 cm的炮孔，炮孔深度为11 cm，如图5所示. 试验以2.5 g的高能导爆索(爆力值A1为480 mL)作为起爆药包，其长径比为3；利用电雷管(爆力值A2为500 mL)起爆导爆索，一发电雷管含0.60 g±0.01 g泰安，利用暴力值换算成0.58 g黑索金，总药量为3.08黑索金. 为使填塞增大摩檫力，利用石膏进行填塞.

2.3 高速摄影系统

在爆破模型试验过程中，常采用高速摄影系统对爆破破坏过程进行观测. 本试验采用NAC的HotShout1280cc高速摄影仪对爆破鼓包运动进行拍摄. 试验采用1 000幅/s拍摄频率、1 024×612分辨率对鼓包运动进行拍摄. 为了方便分析鼓包运动位移，在模型后方设置5 cm×5 cm的方格布，如图6. 将高速摄影仪进行准确对焦后与起爆器同步触发进行拍摄记录.

3 鼓包运动试验结果分析

3.1 鼓包运动分析

使用HotShotLink软件对拍摄的鼓包运动图像进行逐帧播放，每隔2 ms拾取一张图片，图7为模型1#在2～16 ms的鼓包运动图像.

通过对高速摄影所记录的图像对鼓包运动发展过程和破碎形态进行分析；如图7所示，在装药密度相同的条件下，鼓包运动具有很好的重复性. 当炸药发生爆炸时，爆炸冲击波作用于炮孔壁并衰减为应力波，并在0.1 ms内传播到岩体自由面，同时发生反射并与入射波相遇，使自由面产生裂隙，在爆轰气体作用下，岩体裂隙进一步发育，并在自由面产生鼓包运动；2 ms时，在自由面开始出现鼓包，但并不明显，同时自由面出现微小裂隙；对鼓包运动进一步分析；4 ms时，自由面在爆生气体的作用下出现了明显的鼓包，裂隙进一步发育，自由面仍为连续状态；6～8 ms时，自由面出现明显的裂纹，爆轰气体泄漏，鼓包轮廓呈现为规则的“凸”状，以最小抵抗线方向为主导，相对于其他质点先达到最高点；10 ms时，鼓包轮廓仍维持着“凸”状，鼓包裂纹进一步扩大；当到达14 ms时，表面岩体已被彻底破碎，失去规则的“凸”状，自由面达到最高点并失去连续状态，开始呈放射状向四周抛散；16 ms时，自由面鼓包完全破碎，爆轰气体泄漏，鼓包运动逐渐弱化，最后按弹道理论进行运动，爆破漏斗整个抛掷过程持续200～300 ms.

3.2 爆破漏斗效果

在实验中，对4个模型进行逐一爆破后，对爆破漏斗深度、爆破漏斗半径、爆破漏斗体积进行测量，并统计在表3，图8为爆破漏斗效果图.

表3 试验参数

通过分析得到4个试件的爆破作用指数分别为：n1=1.18，n2=1.13，n3=1.06，n4=0.99,即模型1#、2#、3#为加强抛掷爆破漏斗，模型4#为减弱抛掷爆破漏斗，结果表明模型试件均未形成标准的爆破漏斗(n=1).

3.3 鼓包运动速度规律分析

利用HotShotLink软件对高速摄影仪所记录的图像进行逐帧播放，选取模型1#鼓包运动2,4,6,8,10,12,14 ms图像，将不同时刻、不同质点的鼓包运动速度绘制在同一坐标轴，如图9所示.

从图9中可以看出不同时刻的鼓包运动趋势具有良好的重复性，呈现为连续的“凸”字形. 在最小抵抗线方向上，应力波先传播到自由面，并使其产生裂隙；爆生气体随后作用于这些裂隙，使裂隙进一步扩大，自由面中心较其他位置先出现鼓包运动，并达到最大位移. 随自由面炮孔中心距离加大，鼓包隆起的高度也随之降低. 鼓包运动的时间在毫秒单位内完成，将某一时刻鼓包运动平均速度视为瞬时速度，拾取鼓包运动速度，并记录(见表4).

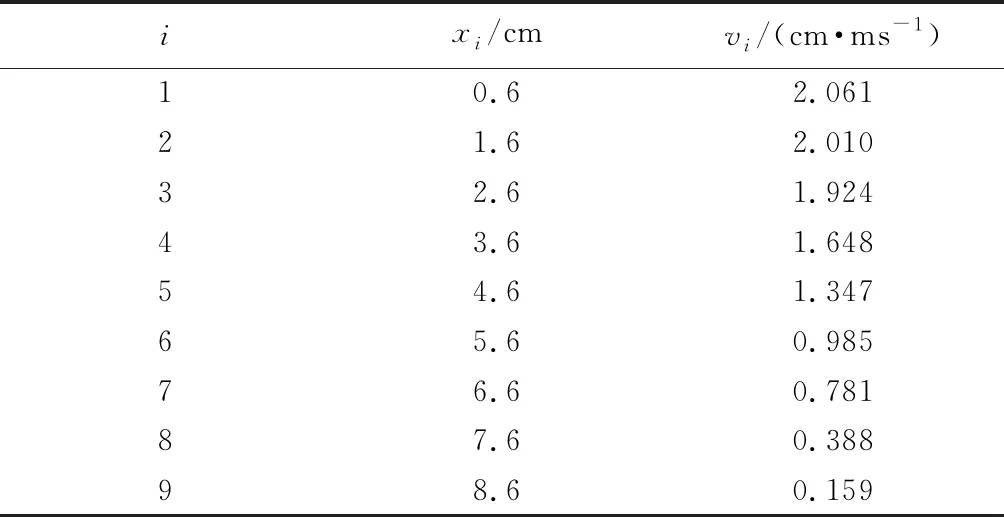
表4 2 ms运动位移

利用Leveneberg-Marquard方法[17]将模型(6)拟合到所得数据，a、b、c最小误差向量的RMSE矩阵为

(11)

在n个数据点上计算r的偏导数为一个8×3的矩阵

(12)

Leveneberg-Marquard使用初始估计(a，b，c)=(1,1,1),λ固定在50，将会得到最优的最小二乘模型:

对2 ms时刻的岩体运动速度进行拟合分析，可得其相关性系数为0.99，表明拟合岩体运动速度具有很高的精确度. 同理对4，6，8，10，12，14 ms运动速度进行拟合(见表5)，并计算出鼓包运动岩体运动速度. 在具体某一时刻，鼓包运动速度服从指数分布.

表5 不同时刻鼓包运动速度拟合式

随自由面鼓包裂隙的不断“发育”，爆生气体泄露，则鼓包运动过程中爆生气体压力不为一个恒量，鼓包运动所受推力也将发生变化，表明鼓包运动为一个变速运动，对表4中不同时刻鼓包运动最大速度进行拟合可得鼓包运动最大速度变化表达式

v(t)=-0.067t2+2.167t-2.342.

(14)

鼓包运动在爆生气体的做用下做变加速运动，当鼓包运动完全破裂时，破碎岩体在剩余爆生气体作用下做抛掷运动，为得到岩体最远抛距，对破碎岩体进行运动速度分析(见图10).

从图10中可以看出，岩体破碎后在爆生气体作用下做弹道运动，向四周抛散，形成扇形抛掷区. 炸药对岩体的作用不仅与岩体性质有关，还与炸药的爆炸荷载与加载速率有关[18]，在理想状态下，不考虑空气阻力与岩石间的碰撞作用[19-20]，岩石在重力作用下做弹道运动. 通过运动分析可以得到理想状态下石块的抛掷距离表达式(15)，对指导工程实际具有重大的意义.

(15)

式中：L为石块的抛掷距离；θ为石块运动速度与水平坐标所成的角度；v为鼓包运动得最大抛掷速度；g为重力加速度.

在岩块的抛掷过程中，当岩块的最大抛掷速度与水平速度成45°时，岩块的抛掷距离达到最大值，具体距离为：

L(xi)=vxt=v2(xi)/g.

(16)

4 结 论

① 通过对爆破作用机理进行分析，运用动量守恒定律对爆破漏斗鼓包运动速度进行分析，并利用最小二乘法原理建立鼓包运动速度理论指数模型，并揭示了鼓包运动以最小抵抗线方向为主导做变加速运动.

② 采用高速摄影仪对爆破漏斗模型鼓包运动进行记录分析，不同时刻鼓包运动速度都服从指数分布，并具有极高的相关性，并随炮孔中心距离的增大呈指数递减；2，4，6，8，10，12，14 ms时，其炮孔中心鼓包速度分别为1.910，4.750，8.551，10.686，12.705，13.971，14.865 cm/ms，表明不同时刻鼓包中心做变速运动，并随炮孔中心距离的增大呈指数递减.

③ 在爆生气体作用下，自由面岩体破碎成规则的扇形状，当自由面鼓包运动完成后，破碎岩块向四周做飞散运动，根据鼓包运动速度模型，结合弹道理论获得自由面碎石的理想飞散距离，对爆破飞石的飞散运动研究具有一定的意义，具有很好的工程指导价值.