基于改进SVM的车辆传动系统故障诊断方法

马立玲，郭凯杰，王军政

(北京理工大学 自动化学院，北京 100081)

车辆传动系统属于整车系统中关键组成部分. 在车辆运行过程中车载监控系统会采集、存储大量用于监测实车运行过程的数据，对传动系统进行故障分类和性能评估. 但是这些数据具有数据量大、维度高、不平衡等特征，使得很多传统的数据分析方法无法满足其需要.

支持向量机(SVM)是一种基于VC维理论和统计学习中结构风险最小化原理的机器学习方法. 与神经网络等传统方法相比，处理小样本、高维数和局部最小值时效果更好.

但是，在处理实际数据集的过程中，传统的SVM算法也存在一些问题. 首先，SVM[1-3]算法对数据集中的噪声、野点和正常样本赋予相同的权重，从而显着降低SVM分类结果的准确性. 此外，大量的实际数据集在样本大小上是不平衡的，在这种情况下，机器学习分类器来自大的负(无关)样本，寻找少量阳性(相关)样本. 传统的SVM算法通常受到优势类数量的偏差，因为它们的损失函数试图优化相关性的数量，例如错误率，而没有将数据分布纳入考虑范围内，甚至忽略少数类样本，从而造成传统 SVM的性能大大下降. 出于这个原因，许多研究人员提出了改进的方法. Lin等[4]提出了模糊支持向量机(FSVM)算法，结合了模糊数学的理论，根据样本数据到该类中心的距离远近，分配给每个训练样本不同的权值，减少了噪声和野点对分类器性能的影响. 同样，张炤等[5]使用内核方法在内核空间中实现FSVM算法；Jiang等[6]提出了一种基于样本之间紧密度的FSVM算法. 为了解决数据集不平衡的问题，Hui等[7]将SVM算法与欠采样或过采样技术相结合，以平衡正负类的采样率. Chang等[8]通过为正样本和负样本分配不同的误差成本(DEC)来减少不平衡数据对SVM算法的影响. 该算法不仅给出了具有不同惩罚因子的正样本和负样本，而且还为约束添加了新的参数，使分类表面更加灵活，提高算法的准确性.

然而，用SVM进行车辆故障分类时，仍然存在一些问题：①单纯用一种SVM改进算法无法同时有效地处理噪声点和数据集不平衡的问题；②FSVM算法在设计模糊隶属度时使用欧氏距离，并且均等地处理样本的不同属性之间的差异；③传统SVM仅仅输出的是故障类别，无法输出正常状态下的故障概率，从而做出故障预警及性能评估. 针对以上问题，本文提出了统一的解决办法. 相比传统的SVM算法优点在于：①能够有效处理数据不平衡问题；②使用马氏距离代替欧氏距离来设计模糊隶属度，消除变量相关的干扰；③增加了正常状态下的故障概率输出模型，便于后续进行车辆传动系统的故障预警和性能分析.

1 基于改进SVM的故障诊断

1.1 惩罚因子(DEC)

传统的SVM 算法认为，每一个样本的重要性是相同的，算法分配给每一个样本相同的权值. 给定训练集(X,T)={(xi,ti),i=1,2,…,l}，其中xi为样本，ti为样本xi的标签；引入非线性映射φ(x)，将训练集映入高维空间(φ(X),T)={(φ(xi),ti),i=1,2,…,l}；选取适当的核函数K(x,y)=φ(x)Tφ(y)；引入松弛变量ξi≥0,i=1,2,…,l. 标准支持向量机的一般形式可表示为

ti[ωTφ(xi)+b]≥1-ξi,

ξi≥0,i=1,2,…,l.

(1)

但在车辆传动系统试验数据集这样的不平衡数据集中，如果给予正负类样本同样的权值，分类结果通常偏向于多数类，并且通常会忽略一些少数类，将其作为多数类的异常. 为此，DEC算法可以通过为较小的类分配较大的权重而为多数类分配较小的权重有效地减少不平衡对SVM算法的影响. 在式(1)中，假设前p个样本是正类样本，后l-p个样本是负类样本. 则变为以下不平衡SVM的一般形式

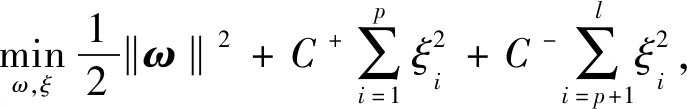
ti[ωTφ(xi)+b]≥1-ξi,ξi≥0,i=1,2,…,l.

(2)

式中：C+和C-分别为阳性和阴性样本的惩罚因子，并提出了一系列方法选择阳性和阴性样本的惩罚因子的比例. 文献[9]将C+/C-设置为多数类与少数类样本个数的比值，文献[10]则搜索包含高维空间中正负样本的所有样本点的超球面，并比较两个球体的半径. 两相比较，计算所有样本点超平面的方法时间复杂度较高，而车辆传动系统试验数据不同样例间的稀疏程度差别不大，再考虑到车辆传动系统试验数据集数据量大，维度高的特点，本文采用文献[9]中的方法，将惩罚因子设置为多数类与少数类样本个数的比值.

1.2 模糊隶属度

惩罚因子为正负类样本提供了不同的权值来平衡正负类样本的类间差异，同样，在同一类中每个样本的重要性也是不同的.

定义正类样本在特征空间的均值为φ+，负类样本在特征空间的均值为φ-，前p个样本是正类样本，后l-p个样本是负类样本，即

(3)

(4)

则正负类在特征空间中的半径分别为

i=p+1,p+2,…,l.

(6)

那么模糊隶属度为

(7)

(8)

引入式(2)中有

ti[ωTφ(xi)+b]≥1-ξi,

ξi≥0,i=1,2,…,l.

(9)

也就是说，训练集中的不同训练样本被给予不同的模糊隶属度(即权重)以测量样本对分类器的重要性.

然而，该方法仅使用从样本到其类中心的欧式距离作为样本重要性的指标. 虽然欧式距离简单易用，但缺点是显而易见的，样本的不同属性之间的差异也是以同样的方式处理，有时不能满足实际需要. 然而，马式距离不受维数影响，可以消除不同变量之间的相关干扰，可以计算样本与不同种群之间的相似性，因此更适合判断故障类别.

1.3 概率输出

标准的SVM的无阈值输出为

f(x)=h(x)+b，

(10)

式中

(11)

Platt利用sigmoid-fitting方法[11]，将标准SVM的输出结果进行后处理，转换成后验概率

(12)

式中：A,B为待拟合的参数；f为样本x的无阈值输出.S形拟合方法的优点在于，在保持SVM稀疏性的同时，可以很好地估计后验概率.

SVM概率输出使得SVM不仅能够用于故障分类，还可以得到正常状态下各个故障的发生概率，从而起到故障预警和性能分析的作用.

2 改进SVM的具体步骤

① 采集原始故障数据，对原始数据进行归一化处理，并将处理后的数据分为两部分：训练集和测试集.

② 根据正负类样本的比例关系为他们设置合理的惩罚因子，用马氏距离代替传统的欧式距离代入式(7)(8)中，为每个样本分配具体的隶属度权值.

马氏距离的表达式为

(13)

式中Σ为两个向量间的协方差矩阵.

由于高维空间中样本点之间存在协方差矩阵的逆矩阵，文献[12]给出了高维特征空间. 不需要求解协方差矩阵的逆矩阵，并且核函数用于求解采样点到类的中心的马尔可夫距离. 代入式(7)(8)中可得

(15)

式中：

(16)

(17)

③ 输入训练集， 使用网络搜索法[13]对惩罚因子C和核参数γ进行寻优，从而达到最好的训练准确度.

④ 用测试集对训练好的SVM模型进行测试和故障分类. 对于正常状态类的数据，通过其概率输出进行故障预警和性能分析.

3 实验与结果分析

3.1 故障分类

本实验依托于某车辆外场试验数据来验证算法的正确性. 该采样数据共有10种不同状态(包括正常状态和9种故障状态，其中9种故障状态分别为：润滑油压异常，发动机乏力，油温过高，闭锁油压异常，风扇转速异常，各档操纵件压力异常(包括2档、5档、中心转向档、倒1档共4个故障状态)). 原始数据包含有44个不同的属性变量，本文选取与故障可能相关的10个属性变量，分别为：润滑油压，传动出油温度，风扇转速，发动机转速，档位，发动机水温，Cb闭锁压力，输出转矩，操纵油压，风扇驱动压力.

由图1可以看出，故障3(油温过高，后文用故障3代替)和故障4(操纵油压异常，后文用故障4代替)的原始观测数据不平衡程度高，空间重叠严重，同时具有很多噪声和野点(特征7、9分别为Cb闭锁压力和操纵油压).

通过对原始采样数据的大量统计，得出故障3和故障4的样本数比例大概在1：20左右. 通过截取一段时间内的采样数据，计算出其中故障3样本50条，故障4样本共996条，比例与统计结果大致相符. 从样本集中随机提取25个故障3数据，500个故障4数据，剩余数据用作测试集. 将本文算法与传统SVM，DEC，FSVM算法分别在该样本集上进行验证和比较，并使用网络搜索法对惩罚因子C和核参数γ进行寻优.

表1 不同算法的故障诊断结果Tab.1 Fault diagnosis results of different algorithms

SVM的理论基础是使用非线性映射将样本映射到高维空间，使他们可线性分离，并使用核函数的思想，满足 Mercer条件的核函数用于替换高维空间点积运算，最后实现分类器设计. 然而，在实际应用中，通常难以在高维空间中获得特定的映射形式.

为了能够可视化SVM分类结果，使用经验特征映射来代替传统的高维特征映射[14]. 对应于核矩阵K的两个最大特征值的两个主方向向量被投影在经验特征空间中.

然后使用本文提出的算法对数据集进行处理，同样在经验特征空间中向核矩阵K两个最大的特征值所对应的两个主方向向量作投影.

从图2和图3的比较可以看出，当传统的 SVM算法处理不平衡数据时，类间距很小，小类样本基本上被多类的样本包围，而改进的SVM算法可以有效地解决数据不平衡问题，有效地增加了类间距. 同时分布尽可能地稀疏，并且在几个类的识别率和整体性能方面优于传统的分类算法.

3.2 概率输出和性能评价

取一段时间内包含故障3、故障4和正常状态的共200条数据作为训练集，在本文的相关向量机模型中训练并输出概率模型. 通过观察正常状态下的概率输出结果，可以评估该时段内不同故障的发生概率，在故障概率过高的故障做出故障预测. 并可以结合层次分析法对传动系统的性能做出分析和评估.

如图4所示，截取60条正常状态下的概率输出数据，将发生故障3和故障4的概率绘制成曲线. 从图中可以看出，在第40～45条数据对应的系统运行时间内，两种故障发生的概率明显高于平均值，可以判定该时间段内系统运行出现异常.

此外，得到正常状态下的各个故障发生概率，也有助于后续利用层次分析法等特定算法对车辆传动系统进行性能分析.

4 结 论

提出了一种新的用于不平衡数据的概率SVM算法. 该算法不仅可以有效地降低不平衡数据对SVM造成的影响，而且用马氏距离设计模糊隶属度， 可以消除变量相关性对分类结果的干扰，并且可以减少数据中的噪声和野点干扰. 数据集的数值实验验证了分类方法的有效性. 同时通过改进SVM输出正常状态下各个故障的概率，可以有效地进行故障预警和性能分析.

然而，应该指出的是，虽然算法提高了分类精度，但是需要优化的参数也增加了. 下一步是设计有效的参数选择策略，以缩短算法的训练时间.