考虑固体颗粒的自由喷流噪声的数值研究

荣吉利，阿尼苏，程修妍，范博超

( 北京理工大学 宇航学院，北京 100081)

近年来，随着火箭导弹以及航天飞行助推器的广泛应用[1]，火箭发动机的高温超音速喷流噪声问题成为了不断被研究的对象，喷流噪声对工作人员、地面设施及有效载荷极具威胁，因此深入研究喷流噪声具有重要意义.

1954年，Lighthill[2]提出了声类比理论，从理论上完成了对喷流发声问题的研究. 随着计算机技术的发展，目前数值模拟已成为喷流噪声问题的主要研究方法. Gamet和Estivalezes[3]于1998年对马赫数2，雷诺数6×104的超音速高温喷流进行了数值模拟，计算结果与试验结果相差不大. 2006年，刘耀峰和徐文灿等[4]数值模拟了喷口附近的流场结构及涡系结构等流场特性，计算结果与实验结果吻合较好. 2017年，马红鹏等[5]对设计的某微型燃烧室的稳态燃烧过程进行数值模拟，得到燃烧室稳态工作时的速度场、温度场及各组分浓度分布，仿真与实验数据契合度高. 孙博等[6]于2018年采用3维黏弹性有限元方法分析了固体火箭发动机点火发射时药柱界面裂纹的稳定性. Troyes和Vuillot[7]于2016年采用大涡模拟方法和Ffowcs Williams-Hawkings方程(简称FW-H方程)分别计算了马赫数为3.1的高温超音速喷流的流场和声场，计算结果误差较小. 2019年，Langenais[8]改进了Troyes和Vuillot[7]的远场噪声求解方法，大大提高了计算结果的精度(几乎所有测点总声压级的误差小于1 dB). 目前广泛使用的固体火箭发动机会产生凝相固体颗粒，但几乎所有关于固体火箭发动机喷流噪声的研究都忽略了固体颗粒对喷流流场和声场的影响.

文中针对Seiner&Ponton喷管模型[9]，选取了6种不同的湍流模型，包括Spalart-Allmatas模型、Standardk-ε模型、RNGk-ε模型、Realizablek-ε模型、Standardk-ω模型和SSTk-ω模型，进行了稳态计算，研究了这6种湍流模型对喷流流场稳态结果的影响；又以RNGk-ε模型的稳态计算结果为初始流场，使用大涡模拟方法(large Eddy simulation，简称LES)计算了该喷管模型的非稳态结果，并使用FW-H方程进行了声场分析，计算结果与试验结果进行了对比；最后在此模型的基础上，添加了固体颗粒，研究固体颗粒对喷流流场及声场的影响.

1 数值模拟方法

1.1 控制方程

在笛卡尔坐标系下，3维可压缩流的N-S方程为

(1)

式中，

(2)

式中：ρ为气体密度；u，v，w分别为x，y，z方向的速度；p为压强；qi为热传导引起的能量通量；τij为应力项.

(6)

式中μ为黏性系数.

单位气体总能量e为

(7)

式中γ为气体比热.

最后再引入理想气体状态方程，

p=ρRT,

(8)

式中:R为气体常数;T为温度. 即构成了封闭的控制方程组.

1.2 湍流模型

Spalart-Allmatas模型是求解湍流黏性输运方程的单方程模型. 此模型适用于低雷诺数模型，不适用于自由剪切流. Spalart-Allmatas模型的输运方程形式为

(9)

Standardk-ε模型对湍动能(k)和耗散率(ε)建立了输运方程. Standardk-ε模型不适用于强分离流、包含大曲率的流动和强压力梯度流动，适用于高雷诺数湍流，是工程计算中应用十分广泛的湍流模型. 湍动能(k)和耗散率(ε)从下列输运方程中得出，

Gk+Gb-ρε-YM，

(10)

(11)

式中:Gk为平均速度梯度产生的湍动能;Gb为由浮力产生的湍动能;YM为可压缩湍流中脉动膨胀对总耗散率的贡献量;C1ε、C2ε和C3ε是常数;σk和σε分别是k和ε的湍流Prandtl数.

RNGk-ε模型是Standardk-ε模型的改进模型，RNGk-ε模型在ε方程中增加了修正项，提高了计算快速应变流的精度；考虑了湍流漩涡；为湍流Prandtl数提供了一个解析公式；使得RNGk-ε模型比Standardk-ε模型在计算更广泛的流动中有更高的可信度和精度.

Realizablek-ε模型也是Standardk-ε模型的改进模型，Realizablek-ε模型为湍流黏度提供了可选公式；修正了耗散率ε的输运方程. Realizablek-ε模型的不足是：在计算同时包含旋转和静态流动区域时不能提供自然的湍流黏度.

Standardk-ω模型基于Wilcoxk-ω模型，考虑了低雷诺数、可压缩性和剪切流传播；该模型的缺点是对来流因素过于敏感；该模型适用于墙壁束缚流动和自由剪切流动；其湍动能(k)和比耗散率(ω)的输运方程为

(12)

(13)

式中Γk和Γω分别为k和ω的有效扩散率.

SSTk-ω模型在近壁面使用Standardk-ω模型，而在主流区域使用k-ε模型；在ω方程中加入了阻尼交叉扩散导数项并且在湍流黏度的定义中包含了湍流剪切应力的传递；这些改进使得SSTk-ω模型比Standardk-ω模型有更高的精度和可靠性.

LES是近几十年才发展起来的一个流体力学中重要的数值模拟研究方法；其基本思想是使用过滤方程滤掉小尺度涡，使用统一模型计算小尺度涡，再使用N-S方程直接求解大尺度涡. 假设用uf来表示流场速度，

(14)

(15)

为了使方程组封闭，需要使用Smagorinsky模型来建立亚格子应力的数学模型.

1.3 数值格式

本文采用密度基求解器来求解控制方程，差分格式选用了Roe通量差分格式.

密度基求解器首先同时求解连续方程、动量方程、能量方程及组分输运方程，再逐一求解其他标量方程. 密度基通常用于高速可压缩流动的求解.

为减少数值耗散造成的误差，准确捕捉激波现象需要采用高阶或者高分辨率的差分格式进行离散，Roe格式是通量差分分裂最具代表性的格式，它以其优秀的间断分辨率，得到了广泛应用[11].

1.4 FW-H方程

1969年，Ffowcs Williams和Hawkings[12]将喷流发声的理论扩展到了任意运动固体边界在流动中发声的问题，即为FW-H方程. 其方程如下,

(16)

式中：ui为xi方向的流速大小;un为积分面法向流速大小;vi为xi方向面速度大小;vn为积分面法向面速度大小;δ(f)为狄拉克(Dirac delta)函数;H(f)为亥维赛(Heaviside)函数;Tij为莱特希尔(Lighthill)应力张量;Pij为可压缩应力张量.

FW-H方程可以计算在流体中流体与运动的物体相互作用而发出声音的问题.

1.5 离散相模型

固体发动机喷流中含有固体颗粒，在流场计算时应考虑固体颗粒的辐射作用，但目前几乎所有关于固体火箭发动机喷流噪声的研究都忽略了固体颗粒对喷流流场的影响. 在进行气-固两相流场的耦合计算时，气相的控制方程相较于只有气相的控制方程，仅多了气固两相相互作用的源项，

式中:Ep为粒子的辐射率;a为介质的吸收系数;ap为粒子的吸收系数;n为介质的折射率;σ为玻尔兹曼常数;G为入射辐射.

通过对粒子受力平衡等式的积分来求解粒子轨迹线

(18)

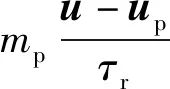
1.6 湍流强度

湍流强度是一种度量气流脉动程度的针对湍流统计规律的描述，用脉动速度均方根与时均速度之比表示为

I=urms/utm.

(19)

2 数值仿真结果分析及验证

2.1 喷管喷流数值仿真模型

Seiner&Ponton喷管模型[9]的出口直径Dj=91.44 mm，出口马赫数为2. 由于文献中没有详细介绍此喷管的几何尺寸，因此参照王克印等[13]提出的喷管设计方法设计了最简单的缩扩型喷管. 具体模型如图1所示，为了超音速喷流可以充分发展以及选取合理的声源积分面，因此计算模型的轴向长度必须足够长；同样径向也需要足够宽以防止边界条件会对流场造成影响，影响计算结果. 结合以上因素的考虑，将计算模型的轴向长度设为50Dj，径向长度设为30Dj.

模型中包含入口边界两个，即燃气入口和空气入口. 按照实验条件，给定燃气入口(即喷管入口)处总温1 375 K，总压780 000 Pa；空气入口总温300 K，总压101 325 Pa. 出口均设置为压力出口；声源面设置为内部边界，声源面形状为逐渐扩张的圆管，沿计算域轴向的长度为25Dj，如图1所示，声源面左侧距喷管出口面0.5Dj，左侧面半径为2Dj，右侧面半径为4Dj. 具体边界条件划分如图1所示.

网格图如图2所示. 整个计算模型均采用结构化网格，网格最小尺度为0.5 mm，位于喷管壁面处，以便可以准确模拟喷管内部流动；在声源面内部加密网格，因为此处为湍流剧烈区域；声源面外使用了逐渐粗糙的网格，可以减小计算量并减小出口界面伪反射波的影响. 总网格数为283万.

2.2 不同湍流模型稳态计算结果对比

以此计算模型为基础，分别使用6种不同的湍流模型，包括Spalart-Allmatas模型、Standardk-ε模型、RNGk-ε模型、Realizablek-ε模型、Standardk-ω模型及SSTk-ω模型，计算了Seiner&Ponton喷管模型的稳态流场.

图3展示了不同湍流模型的稳态数值结果中轴向对称界面流场马赫数分布云图，几种湍流模型都能计算出喷流的压缩膨胀波系，且膨胀、压缩的位置几乎相同，但是喷流的膨胀压缩波系的波节数以及湍流核心区域的长度存在着明显的不同；几种湍流模型中，RNGk-ε模型得到的湍流核心区域最长，且波节最多最为明显；Spalart-Allmatas模型核心区域最短，波节最少.

图4分别对比了不同湍流模型计算结果轴线上的马赫数、压强以及温度，不同湍流模型的计算结果总体趋势大致相同，马赫数及压强在约10Dj前呈现震荡变化趋势，随后快速下降. 其中，Spalart-Allmatas模型的衰减最快，经历3个周期后便开始衰减，而RNGk-ε模型衰减最慢，约经历5个周期后衰减.

Varnier[14]通过一系列试验得出的超音速段长度经验公式为

(20)

式中Maj为出口马赫数.

表1展示了6种湍流模型计算结果流场的超音速段长度，针对此模型，式(20)计算结果为18.21Dj，RNGk-ε与Standardk-ε的计算结果与式(20)计算结果最接近. 再考虑到RNGk-ε为Standardk-ε的改进模型，接下来将以RNGk-ε计算的稳态流场为初始流场来继续进行计算.

表1 不同湍流模型的超音速段长度

图5给出了以RNGk-ε模型计算结果的轴向对称截面流场各参数分布云图，喷流的流场内部是由一系列膨胀压缩波组成的.

2.3 LES非稳态计算结果

以RNGk-ε模型的计算的稳态结果为初始流场，使用LES湍流模型计算了该喷管模型的非稳态流场，使用的时间步长为5×10-6s.

图6给出了非稳态计算至0.2 s时，模型轴向对称截面流场的各参数分布云图. 与稳态计算结果(如图5所示)对比可得，前5个波系结构，流场结构几乎一致，但随后气流变得杂乱无章.

对非稳态计算结果轴线上的速度进行了统计平均，再将轴线上平均速度分布以喷管出口速度vj为参考得到了轴线上量纲一速度分布，以便与试验数据进行对比. 图7展示了轴线上的量纲一速度分布，与Seiner等[9]的试验数据进行了对比，数值计

算结果与试验数据十分接近，证明了数值计算结果的合理性.

2.4 声场计算结果

非稳态计算至喷流充分发展(湍流特性完全显现)后，在非稳态流场的基础上继续进行计算，并保存所选取的声源面上的流场脉动信息(每10个时间步保存一次信息)，再使用FW-H方程预测远场声学特性. 将声场计算结果与Seiner等[9]的试验数据进行对比，验证计算结果的正确性.

参照Seiner等[9]试验方案中布置噪声测点的位置，在此计算模型中设置了噪声测点，设置噪声测点的具体方式是：如图8所示，以喷管出口中心点为圆心，在模型的轴对称平面上取一半径为40Dj(3.66 m)的半圆，设喷流方向为0°，在此半圆上，从0°～180°每隔10°便设置一个噪声测点，共设置19个噪声测点.

将20°和50°噪声测点的1/3倍频程谱与试验数据进行对比，如图9所示. 计算结果与试验数据的变化趋势大体一致，最大误差约为5 dB，在工程可接受的范围内.

计算各个噪声测点处的总声压级，并将计算结果与Seiner等[9]的试验数据对比，如图10所示，在远场半径为40Dj的半圆上，声压级最大值为149.94 dB，位于50°的测点处，试验数据的最大值也大约出现在50°测点处，计算结果与试验数据的变化趋势相同，60°～100°之间，数值计算结果与试验数据基本一致，在20°～60°之间，数值计算结果存在一定的误差，最大误差约为6 dB. 但在20°～60之间数值计算的结果与Biancherin[15]使用FW-H计算的结果十分接近，差别在2 dB以内，且比Biancherin[15]的计算结果更为接近试验数据.

误差出现原因主要有：①数值计算模型的环境条件与试验的环境条件存在差别，因此会出现一定的误差；②此喷管出口喷流马赫数较高，对网格的质量要求较高，可以进一步加密网格来减小误差；③由于没有Seiner等[9]试验喷管的详细结构，数值计算所用喷管模型是自行设计的构型简单的喷管，会对流场计算结果产生影响，也导致了一定的误差.

但综合流场对比、单点声压级频程谱对比以及测点总声压级对比来说，数值计算的流场、声场结果还是比较准确的.

3 固体颗粒对喷流流场、声场的影响

3.1 固体颗粒对喷流流场的影响

以RNGk-ε模型的计算结果为初始流场，以喷管出口面为固体颗粒释放面，进行稳态计算，获取固体颗粒对喷流流场的影响，固体颗粒相关参数如表2所示.

表2 固体颗粒参数Tab.2 Solid particle parameters

表中:ρp为颗粒密度;Dp为颗粒直径;Cp为颗粒的定压比热;ep为辐射率;qmrp为颗粒的质量流量.

对固体颗粒做出如下假设[16]：①气体与颗粒之间不考虑化学反应；②颗粒间无碰撞等相互作用；③颗粒形状为球形.

含固体颗粒的喷流流场明显与无颗粒喷流流场不同，含固体颗粒的喷流的超音速段长度为16.51Dj，较无固体颗粒的超音速段长度减小了2.6Dj，图11分别对比了有无固体颗粒仿真模型的计算结果轴线上的马赫数、压强以及温度，加入固体颗粒后，燃气与固体颗粒相互作用，使得燃气喷流膨胀做功增大，导致喷流的膨胀压缩波数减少，马赫数迅速衰减，温度升高.

3.2 固体颗粒对喷流声场的影响

以固体颗粒的稳态流场为初始流场，使用LES计算该模型的非稳态流场，计算足够时间后，保存所选取的声源面上的流动参数，再使用FW-H方程预测远场声学特性.

在此计算模型中设置了与无固体颗粒非稳态计算模型位置完全相同的声源面及噪声测点以方便对比，图12对比了有无固体颗粒时远场噪声测点总声压级分布的情况.

0°～30°范围内，有固体颗粒噪声测点的总声压级大于无固体颗粒噪声测点的总声压级. 0°～30°处于喷流的下游，喷流下游噪声的主要成分为湍流混合噪声[17]. 湍流混合噪声与湍流强度成正比例增加，因此对比了有无固体颗粒喷流轴线的湍流强度，如图13所示，在27Dj处，有固体颗粒喷流的湍流强度达到了0.8，远大于无固体颗粒喷流的湍流强度，因此导致了在喷流下游处有固体颗粒声压级较大.

40°～180°范围内，有固体颗粒噪声测点的总声压级低于无固体颗粒噪声测点的总声压级. 40°～

180°为喷流的中上游区域，噪声的主要成分为宽频激波噪声[17]，宽频激波噪声与激波强度成正比例增加[18]. 有固体颗粒喷流的马赫数小于无固体颗粒喷流的马赫数，且超音速段长度较短，即有固体颗粒喷流的激波强度较小，导致了喷流中上游区域噪声较小.

4 结 论

针对Seiner&Ponton喷管模型，建立了3维喷流数值模拟方法，进行了远场噪声分析，并考虑了固体颗粒对喷流流场和声场的影响，得到了以下结论：

① RNGk-ε模型最适合用于稳态喷流数值模拟；

② 使用FW-H方程计算远场噪声的误差有一定的准确性；

③ 固体颗粒的存在减小了喷流流场的超音速段长度，增大了膨胀压缩半径，提高了喷流温度；

④ 在喷流下游区域，由于固体颗粒的存在，增大了喷流的湍流强度，导致喷流下游区域噪声增大，在喷流中上游区域，减小了喷流的激波强度较小，导致中上游区域噪声降低.