考虑轮辙相干性的两种随机路面IFFT生成算法

王汉平，张哲，廖小华

(北京理工大学 宇航学院，北京 100081)

路面不平度的模拟方法主要有谐波叠加法、IFFT法、白噪声滤波法、AR/ARMA法和基于分形理论的模拟法等[1]，但在推广应用于2维路面不平度生成时，这些方法却存在较大的差异. Zhang Yonglin[2]基于文献[3]给出的轮辙相干模型利用白噪声滤波法将相干函数近似成轮辙间的传递函数，构造了2维的时域路面不平度；Wang X[4]和孙宁[5]对谐波叠加法中谐波叠加组分的相位角进行了优化，从而使模拟路面的统计功率谱密度(PSD)更符合标准PSD；Szöke D 等[6]基于IFFT方法提出了一种不同轮辙相位角与相干函数之间的相关关系，仿真结果表明改进的相关关系具有更好的模拟效果；任宏斌[7]和王亚[8]分别基于IFFT方法和谐波叠加法采用拟合的方式获得了左右轮相位角的相关特性，其实施过程未加详述，从相位角相关性的表达形式上看，可能借鉴了文献[6]的思想；荣吉利[9]和朱兴高[10]分别基于有理滤波获得了不同轮辙的不平度特性和履带对路面的包络特性；卢凡[11]则将有理传递函数与相干函数之差构造成目标函数，借助优化来拟合左右轮的相干函数，从而实现轮辙间的滤波器设计，最终获得左右轮路面的不平度特性. Liu Xiandong[12]基于IFFT方法，通过将左右轮的不平度特性分解为原始不平度和扰动不平度，并假定左右轮的原始不平度完全相同，左右轮的扰动不平度完全独立且与原始不平度无关，然后借助PSD和左右轮的相干函数来独立生成原始不平度和左右扰动不平度，最终叠加得到左右轮的不平度特性，但与参考标准的对比可以看出，其模拟精度差强人意；李倩[13]在谐波叠加法的基础上根据PSD及相干函数的定义推导了不同轮辙谐波叠加组分相位角之间的解析关系，并由此构建了通用的二维路面仿真模型，仿真结果验证了模型的有效性，但该模型的计算量较大；BogsjöK[14-15]针对不同路面的测试数据拟合了左右轮辙的相干特性，发现均符合指数衰减规律，在车辆振动损伤模拟方面，这种指数衰减规律的相干函数模型相较于各向同性的相干模型精度明显要高.

以上文献表明，2维随机路面的生成主要从两方面入手：①通过叠加组分相位角的相干关系；②通过不同轮辙间的传递函数关系. 但这些2维路面仿真模型或没公开原始推导，或模拟精度偏低，或算法是时域而非空间域，或算法本身存在不足，亦或计算量较大，这给工程应用带来某些不便. 由此，本文以功率谱密度(PSD)函数、相干函数同不平度函数傅里叶变换之间的关系为基础，理论推导了IFFT法中不同轮辙相位角的相干关系，同时也验证IFFT法与谐波叠加法的等价性；还借助不同轮辙功率谱密度阵的LU分解得到白噪声滤波的传递函数阵，进而分别基于轮辙相位角相干关系和轮辙功率谱密度阵LU分解构造了两种2维路面的IFFT生成模型. 两模型均基于空间域，且仿真速度快捷，最终的仿真对比验证效果良好，从而为2维不平度路面的生成提供了两种高效高精度的仿真模型.

1 基于轮辙相位角相干性的模拟算法

路面不平度特性可当做均值为0的平稳随机过程，通常采用路面功率谱密度函数来描述其统计特性，国际通用标准是将路面不平度分为A至H共8级，其功率谱密度函数的表达式为

(1)

式中：n为空间频率，n0为参考空间频率，通常取0.1 m-1，Gq(n0)为参考空间频率下的路面不平度系数，不同等级的路面其取值不同；w为频率指数，一般取2.

假设左轮的路面不平度曲线为fL(x)，则可知其傅里叶变换为

(2)

根据自相关函数的定义可知，左轮轮辙路面不平度的自相关函数为

由于功率谱密度函数与自相关函数是Fourier变换和反Fourier变换的关系，考虑到路面谱是单边谱，则可知左轮路面的功率谱密度函数为

(4)

于是

(5)

同理

(6)

式中：φL(n)，φR(n)∈[0,2π]均匀分布随机数. 于是，分别对FL(n)，FR(n)进行逆Fourier变换(IFT)即可得到左、右轮轮辙路面不平度函数;

(7)

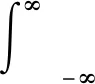
(8)

考虑到计算效率，在进行IFT计算时，可以使用快速逆Fourier变换(IFFT)算法，这就是路面不平度生成的IFFT方法.

将式(7)(8)代入式(4)，可得GLL(n)、GRR(n)为

Gq(n)e[φL(-n)+φL(n)]I,

(9)

Gq(n)e[φR(-n)+φR(n)]I.

(10)

由式(1)可知，Gq(n)=Gq(-n)，所以只有φL(-n)=-φL(n),φR(-n)=-φR(n)时，GLL(n)=GRR(n)=Gq(n)，于是式(7)、(8)可改写为

(11)

(12)

将式(11)(12)与文献[11]中的谐波叠加法对比，只要Ldn≈LΔn=1，则IFFT法与谐波叠加法是等价关系，若左右轮不平度的相干函数为coh(n)，于是可知：

φL(n)=φR(n)+sgn(φ(n))arccos(coh(n)),

(13)

式中：φ(n)∈[-0.5,0.5]是均匀分布的随机数，sgn是符号函数，即左右轮相位角的相干关系.

2 基于轮辙功率谱密度阵LU分解的模拟算法

文献[16]表明，不同轮辙不平度的功率谱矩阵为

(14)

文献[14-15]经过大量试验给出了一种描述不同路面和轮距的路面不平度相干函数，

(15)

式中：B为左右轮的轮距，ρ为跟路面有关的经验值，由此可知coh(n)∈[0,1]. 所以式(14)中的谱阵可进行矩阵分解，且分解为一个矩阵与其转置的乘积，即G(n)=H(n)·HT(n)，文献[17]给出了一种解：

(16)

但该矩阵解中没有哪一个轮辙的谱是独立于coh(n)的，不利于构造具有轮辙相关性的2维路面. 这里提出一种基于LU分解的解，将不同轮辙的谱阵分解为一个下三角阵与其转置的乘积，解为

于是，可以构造两个相互独立、谱值为1的白噪声w1(x)、w2(x)，其对应的傅里叶变换为W1(n)、W2(n)，假设不同轮辙的谱阵是两个白噪声在H(n)滤波下生成，则

(18)

由随机振动理论可知，式(18)中左右轮不平度的谱阵就是式(14)，于是，对式(18)进行逆傅里叶变换，即可得到左右轮的不平度曲线,

(19)

(20)

式中θL(n)、θR(n)∈[0,2π]为均匀分布随机数.

3 路面生成及结果检验

针对相位角相干性模型，由式(12)(15)可得,

f(x,y)=

(21)

针对不同轮辙功率谱阵LU分解的模型，由式(20)、(15)可得

(22)

这就是两种路面不平度生成的IFFT模型，利用Matlab按式(21) (22)编写了两种IFFT路面不平度曲面生成程序，用两种方法对不同等级路面进行了大量的仿真验证，模拟所得的路面功率谱与标准谱完全吻合，左右轮相干性与参考函数也具有很好的一致性. 篇幅所限，不便一一列出，在此仅就ρ=1时的D级路面(即Gq(n0)=1 024×10-6(m2/m-1))的仿真情况进行展示. 图1所示路面纵向长度L=1 000 m，轮辙距离B=2.5 m，路面等级为D级，空间频率范围为0.011～2.830 m-1，垂向偏移为0 m的两方法生成的两轮辙路面不平度曲线，其中模型Ⅰ指基于不同轮辙相位角相干性的IFFT模型，模型Ⅱ指基于不同轮辙功率谱阵LU分解的IFFT模型.

图2和图3分别是在3维路面中截取的轮距B=2.5 m、ρ=1的左右轮轮辙功率谱密度和相干函数的仿真曲线与标准参考曲线的对比，从中不难看出，自功率谱几乎重合，而不同轮辙间的相干函数也符合较好，这从侧面验证了本文推导的左右轮轮辙相位角的相干性关系以及由左右轮轮辙功率谱阵LU分解得到的传递关系是合理可信的. 图3中两模型的仿真相干性与指定参考函数及二者间均存在一定差异，其原因在于两模型都是随机模拟，在相干性方面确实容易出现离差，这是随机模拟无法规避的问题.

4 结 论

基于IFFT法构造了左右轮路面不平度特性，并根据左右轮不平度特性推演了左右轮轮辙的自功率谱和相干关系，由此得到路面重构的IFFT法当Ldn≈LΔn=1时，其与谐波叠加法是完全等价的关系，进而借此获得IFFT法中不同轮辙相位角的解析关系；同时也基于轮辙功率谱密度阵的LU分解得到了白噪声滤波传递函数的解析表达，对不同轮辙不平度的Fourier函数进行逆Fourier变换即得不同轮辙路面不平度曲线. 两种IFFT模型均是解析模型，具有理论上的合理性；仿真结果表明，两模型中各轮辙的自功率谱与标准功率谱吻合较好，轮辙间的相干性也与参考模型具有较好的一致性，从而验证了基于左右轮相位角相干关系的IFFT模型和基于功率谱密度阵LU分解的IFFT模型也具有较好的仿真可信性，它们都能很好地用于2维路面不平度的数字模拟.