让“减速带”成为“机械刷题”的“减速剂”——兼谈2021年高考全国理综甲卷第24题评析

孙鹏伟 于 勇

（西安交通大学附属中学 陕西 西安 710043）

1 问题的起因

【例题】（2021年高考全国理综甲卷第24题）如图1所示，一倾角为θ的光滑斜面上有50个减速带（图中未完全画出），相邻减速带间的距离均为d，减速带的宽度远小于d；一质量为m的无动力小车（可视为质点）从距第一个减速带L处由静止释放.已知小车通过减速带损失的机械能与到达减速带时的速度有关.观察发现，小车通过第30个减速带后，在相邻减速带间的平均速度均相同.小车通过第50个减速带后立刻进入与斜面光滑连接的水平地面，继续滑行距离s后停下.已知小车与地面间的动摩擦因数为μ，重力加速度大小为g.

图1 例题题图

（1）求小车通过第30个减速带后，经过每一个减速带时损失的机械能；

（2）求小车通过前30个减速带的过程中在每一个减速带上平均损失的机械能；

（3）若小车在前30个减速带上平均每一个损失的机械能大于之后每一个减速带上损失的机械能，则L应满足什么条件？

2 问题的提出

考生：第24题设置的“减速带”问题情境成为我答题中的“拦路带”.

命题专家：能否让“减速带”成为“机械刷题”的“减速剂”？

3 问题的回应

一线教师：备考复习中以考查学生对牛顿第二定律、机械能、功、动能定理等核心物理概念、规律理解和运用的试题不知“练习”了多少道.学生不应该使“减速带”问题情境成为答题中的“拦路带”.学生不应该“栽”在“减速带”的问题情境上.

命题专家：今年试题注重“创设真实问题情境，引导学生加强学以致用”，引导教学减少死记硬背和“机械刷题”的现象，助力高中育人方式改革［1］.

4 问题的解决

方法一：从物理模型视角层层剖析问题情境，建构物理模型.

将真实的问题情境转化为物理问题，将物理问题转化为物理过程或物理运动，进而建构起相应的“物理模型”.为此：

（1）建构小车“经过相同位移平均速度相同”的“匀变速直线运动模型”

假设小车通过第30个减速带后的速度为v1，到达第31个减速带前的速度为v2，经过第31个减速带后的速度为v3，到达第32个减速带前的速度为v4，在相邻减速带间运动的加速度为a.

根据题意有

联立求解上式可得

即小车从通过第30个减速带后开始：经过每一个减速带后的速度都相等且等于v1；在到达下一个减速带前速度都相等且等于v2.

（2）建构小车在相邻传送带间运动的“机械能守恒”模型

根据机械能守恒得

结论1：小车通过第30个减速带后经过每一个减速带上损失的机械能

（3）建构小车在水平面运动的“匀减速直线运动”模型

假设小车经过第50个减速带后瞬时速度v50，根据动能定理得

（4）建构小车通过前30个减速带的过程机械能损失的“能量守恒”模型

假设小车通过前30个“减速带”损失的机械能ΔE损30，根据能量守恒得

结论2：小车通过前30个减速带的过程中在每一个减速带上平均损失的机械能

结论3：若小车在前30个减速带上平均每一个损失的机械能大于之后每一个减速带上损失的机械能，则L应满足条件

方法二：从物理本质视角逐项分析问题情境，科学推理论证.

（1）依据“光滑斜面、相邻减速带间距相等”的条件：根据牛顿运动定律可得，小车运动的加速度相等，小车通过第30个减速带以后在相邻减速带间运动速度的增加量相等；根据机械能守恒定律可得，小车在相邻减速带之间运动动能的增加量相等.

（2）依据“在第30个减速带后运动的平均速度相等”条件：根据匀变速直线运动规律可得，小车在经过第30个减速带以后的运动规律具有周期性与重复性.即到达每一个减速带前速度相等；小车经过每一个减速带后速度相等，且等于经过第50个减速带后瞬时速度；小车在每一个减速带上损失的机械能都相等，且损失的机械能等于小车在相邻减速带间运动的重力势能减少.

结论1：小车通过第30个减速带后，在经过每一个减速带上损失的机械能

或选“小车经过第30个减速带后至刚好经过第50个减速带”的运动为研究过程，根据“能量守恒”可得

结论2：依据“小车通过第50个减速带后在水平地面上继续滑行距离s停下”的条件，根据“能量守恒”可得

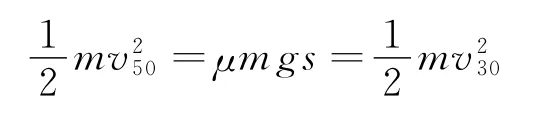
结论3：小车通过前30个减速带的过程中，在每一个减速带上平均损失的机械能

（3）依据“小车通过减速带损失的机械能与到达减速带时的速度有关”“小车在前30个减速带上平均每一个损失的机械能大于之后在每一个减速带上损失的机械能”的条件，结合“第30个减速带后在经过每一个减速带上损失的机械能都相等”的结论，从能量的角度可以推得：

无动力小车沿光滑斜面下滑经过减速带损失的机械能与到达减速带时的动能大小有关，且动能越大损失的机械能就越大，但随着小车到达减速带时的动能逐渐减小，小车经过减速带损失的机械能有趋近“稳定”的态势，当通过第30个减速带后，小车经过减速带损失的机械能达到“稳定”.由此，小车到达第1个减速带时的动能一定大于到达第31个减速带时的动能.即

【试题改编】如图2所示，一倾角为θ的足够长光滑斜面上有足够多个减速带（图中未完全画出），相邻减速带间的距离均为d，减速带的宽度远小于d；一质量为m的无动力小车（可视为质点）从距第一个减速带L处由静止释放.已知小车到达减速带前的速度越大，通过减速带损失的机械能就越大.观察发现，小车到达斜面底端前已处于“稳定”状态.小车通过最后一个减速带后立刻进入与斜面光滑连接的水平地面，继续滑行距离s后停下.已知小车与地面间的动摩擦因数为μ，重力加速度大小为g.

图2 改编题图

（1）求小车“稳定”后，经过每一个减速带时损失的机械能；（mgdsinθ）

（2）若小车在“稳定”前经过每个减速带上损失的机械能大于“稳定”后经过每一个减速带上损失的机械能，则L应满足什么条件？

5 问题的启示

培养学生将“真实问题情境”转化为“物理模型”的能力，在《普通高中物理课程标准（2017年版）》（以下简称“新课标”）的学业水平要求中明确提出：将实际问题中的对象和过程转换成所学的物理模型，能通过建构物理模型来研究实际问题［2］.在《中国高考评价体系》中也特别强调：高考围绕学科主干内容，……通过设置真实的问题情境，考查学生灵活运用所学知识分析解决问题的能力，……使“死记硬背”“机械刷题”“题海战术”的收益大大降低，引导学生的关注点从“解题”向“解决问题”、从“做题”向“做人做事”转变［3］.为此，人教版新教材依据《新课标》的理念，无论是在知识内容上还是章节后的练习中都体现出注重对物理知识的综合运用，注重通过建构物理模型来研究实际问题.例如，人教版《物理·必修》第一册（2019.6）中的“匀变速直线运动的研究”一章，在例题和章节后练习中共设置了14个以“贴近生活、贴近时代”并具有“中国特色”的“科技前沿”发展成就的实例情境，从嫦娥三号登月探测器平稳落月情境到计算触月速度；从航母舰载机起降装置情境到计算弹射装置起飞及阻拦索降落航母跑道长度；从神舟系列飞船运动返回情境到计算着地前减速的加速度；从动车铁路边的里程碑及动车内电子屏幕显示的数据情境到计算动车瞬时速度；从机动车辆刹车情境计算汽车行驶安全距离；从肇事汽车在路面上留下车轮滑动的痕迹到判断汽车是否超速；从人看到红灯时的反应时间到确定骑自行车经十字路口提前刹车减速的距离；从高速公路上不停车的“ETC”电子收费系统的路面标识情境到计算汽车通过的时间等等，这些真实问题情境，在注重培养学生的爱国情感、社会担当、创新精神和实践能力的同时，都是培养学生通过将“真实问题情境”转化为“物理模型”解决实际问题的能力.

年年有高考，岁岁题不同.在每年的高考中广大教师期望考生“重在必得”的第24题，今年不仅没得而且让“减速带”成为考生理综答题的“拦路带”.痛定思痛，期望以注重“创设真实问题情境，引导学生加强学以致用”的高考试题，切实引导教学减少死记硬背和“机械刷题”的现象，更期望能够起到助力高中育人方式改革.