关于前沿研究融入电动力学课程教学的探索

伏洋洋 董大兴 刘友文

（南京航空航天大学理学院 江苏 南京 211106）

电动力学作为一门经典的理论物理课，很多学生由于基础没有打牢，在面对电动力学课程中大量的数学推导，抽象的物理概念时，会觉得难以理解而逐渐失去学习兴趣［1］.

另外，教学内容过于陈旧，也很少联系实际的问题，学生很难有机会运用所学的知识解决一些具体问题，这在一定程度上也降低了学生的学习兴趣.如何改进电动力学课程的教学模式，提高学生的学习体验，促进师生之间的互动交流成为亟需解决的问题［2］.

1 在教学中融入前沿研究的优势

事实上，每位教师或多或少了解一些与电动力学基础理论有关的前沿科学研究，完全可以将一些合适的前沿成果融入到电动力学课程教学中.比如，在光学领域蓬勃发展的等离激元光学、光子晶体、变换光学、超构材料、超构表面等前沿研究方向，更是与电动力学的教学内容紧密联系.在这些前沿研究中，利用计算软件（比如MATLAB）和数值仿真软件（如COMSOL MULTIPHYSICS，简称：COMSOL）计算电磁场特性、呈现物理图像也成为主流手段.这些科研工具完全可以引入到电动力学的教学中去.M ATLAB强大的数学处理能力可以实现抽象“物理问题”可视化［3］，能够让学生在脑海中呈现清晰的物理图像，对“不可见的”电磁场形成有效的认知.CO MSOL则充当“虚拟实验”的角色，可以对具体理论模型的电磁场问题进行仿真模拟［4］，用以检验理论的正确性，有效避免了真实实验中的操作繁琐、体验效果差等缺点.

通过在电动力学教学中引入前沿研究成果，并以科研软件M ATLAB和CO MSOL作为辅助工具，可以有效帮助学生直观地观察电磁现象，越过电动力学概念抽象不易理解的门槛，拓展科学视野，并可以进一步培养学生发现问题、思考问题、解决问题的能力.本文将结合一些超构材料研究领域的前沿进展，探讨如何在电动力学教学过程中融入相关的前沿科研成果，激发学生们的探索热情，增强学生对相关基础知识的深入理解，潜移默化地培养学生的科学素养.下文给出一些具体教学实例，希望能够给予读者一些启发.

2 静电教学实例

2.1 静电隐身斗篷

以《电动力学》（第三版 郭硕鸿著）教材第二章静电场第3节拉普拉斯方程习题2为例：求解介电常数为ε1的介质球置于均匀外电场时的电势分布，如图1（a）所示.由拉普拉斯方程得到介质球内外电势的通解，利用边界条件，可以求出介质球内外区域的电势和电场强度.如果学生仅仅满足数学求解过程而无法清晰理解物理本质，电动力学对于学生来说便只是一门复杂的数学课程.

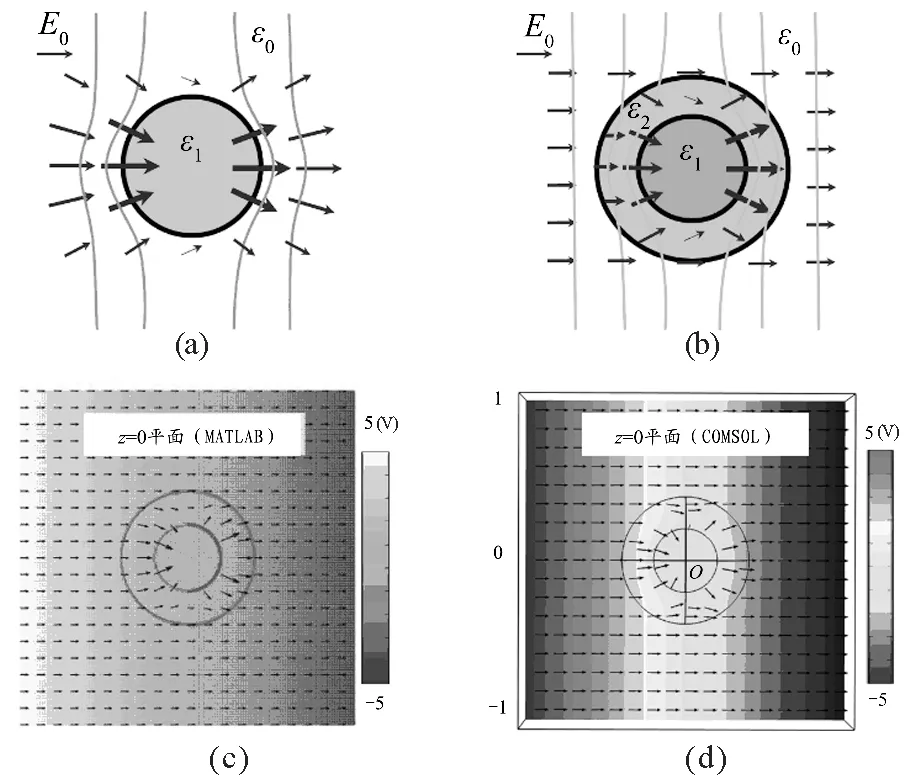
图1 介质球壳结构实现静电隐身M ATLAB理论计算和CO MSOL数值仿真

回到例题，我们得到了球内外电势的解为

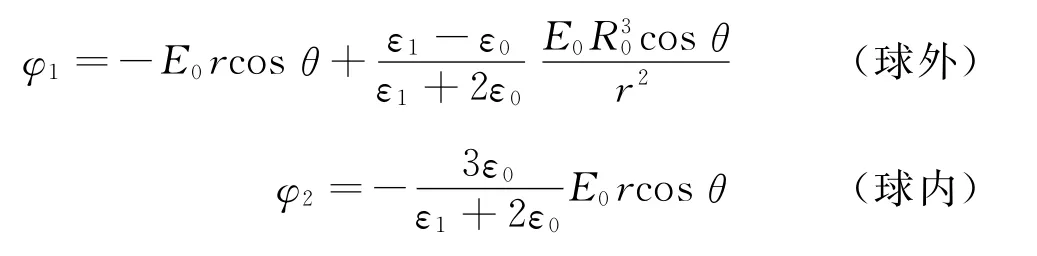
其中，R0为球半径，r为空间点到球心的距离（球心为坐标原点），ε0为真空介电常数，E0为背景静电场大小.从该结论出发，我们可以考虑到两种极端情况：

（1）ε1→-∞，此时介质从数值计算上可近似被看作金属对待，因而在静电平衡条件下，球内不再有电场且电势为零.

（2）ε1=ε0，即介质球被空气代替时，介质球对源场的影响不复存在，我们对各处电势的计算回归到φ=-E0rcosθ.由该点出发，我们可以启发学生进行思考，是否能够设计出一种球壳结构，即在介质球外加另一层介质球壳，最终使球外的电场依然为匀强电场，如图1（b）所示.此时，我们便无法从外部电场的分布判断介质球是否存在，这也就是所谓的静电隐身效果［5］.如前文所述，将拉普拉斯方程的通解求解过程拓展到该球壳结构，可解出结构外的电势分布为

其中

为散射势场系数，ε2为球壳层的介电常数,为球壳内外半径比（a和b分别为球壳内半径和外半径）.当散射电势分布为零（D=0），即达成了静电隐身条件.假定内核球设定为金属时（ε1→-∞），静电隐身条件满足

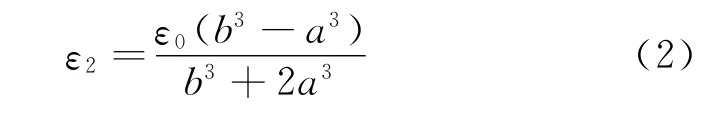
通过该隐身条件，利用M ATLAB可以呈现理论计算的静电隐身的“物理图像”.进一步地利用相关参数，结合CO MSOL的模拟实验可以验证理论计算的有效性.图1（c）与图1（d）是分别使用M ATLAB和CO MSOL展现的球壳在空间中引起的电势变化及电场强度（颜色分布表示空间电势变化，黑色箭头表示电场方向），可以观察到中心金属电势为零，而空间电势分布以及电场强度分布在球壳结构外是均匀的，所有扰动只存在其内部，因此实现了静电隐身的效果.基于此，和学生一起探讨该静电隐身的物理本质是分布在两个内外球面上束缚电荷的等效“偶极子”散射相消的结果.因此，前沿研究在帮助学生深入理解课本例题的同时，也提升其创新意识和能力，对学生今后的学习及科研工作大有裨益.

2.2 静电场下的有效媒介设计

除静电隐身问题之外，我们也可选择性地启发学生探讨静电场下的有效电介质设计研究.在研究静电隐身模型时，我们可以引导学生发现：无论单层介质球还是双层介质球壳外的电势总是有着相似的表达式cosθ.该表达式由两部分构成，即背景电势和介质球引发的散射电势.若将单层介质球和双层介质球壳散射势场系数进行等量匹配，则二者将具有完全相同的电磁响应.物理上来讲，双层介质球壳中的复合电磁参数等价为相同尺寸单层介质球中的均匀有效参数

比如，在设定球壳内外层材料由二氧化硅和银构成（假定二氧化硅的相对介电常数为2.42，银为-4.7），只改变球壳内外半径之比，其等效介电常数可以被有效调节.

图2（a）和（b）分别是M ATLAB计算的球壳结构（内层为二氧化硅，外层为银；内层为银，外层为二氧化硅）的等效介电常数，自变量k为内外半径比.可以发现，该等效介电常数是可以通过控制半径比调整的，扩大了可用电磁参数的范围，也为新型电磁材料的产生提供了渠道.比如，我们以内层为银，外层为二氧化硅为例［图2（b）］，当内外半径比为0.5时，球壳的等效介电常数为-3.1.图2（c）和（d）是基于CO MSOL数值仿真的有等效介电常数的介质球和复合参数的球壳结构对相同均匀静电场响应的模拟场图，二者完全相同（颜色分布表示空间电势分布，黑色箭头表示电场方向，坐标原点位于球心），证实了基于M ATLAB中的理论计算.该仿真计算相对简单，学生们极易上手，能够帮助学生充分理解等效电磁参数的意义.

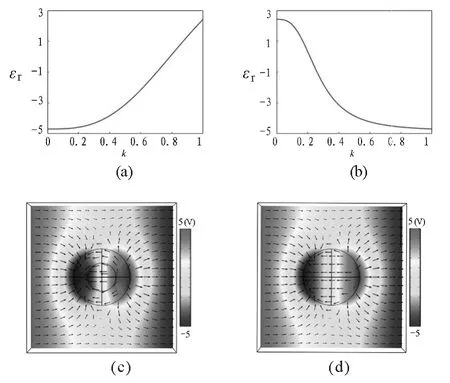
图2 介质球壳结构的等效介电常数MATLAB计算和COMSOL数值仿真

3 电磁波传播教学实例

3.1 奇异介质界面的透反射

电磁波传播作为电动力学教学内容的重要部分，绝大多数教材都会讲述电磁波在均匀介质、有耗介质、两种介质分界面和受限空间（矩形波导）等系统中的传播性质.以电磁波在介质界面反射、折射一节为例，通过菲涅尔公式，学生学习了不同偏振下的反射系数和透射系数，了解了典型的光学现象，如布儒斯特角、全反射等.如图3（a）所示，这里可以进一步引导学生掌握有限厚度的电介质平行板的反射系数和透射系数

其中Z为阻抗，对于横电（TE）偏振，Z=对于横磁（TM）偏振，Z=为介质中垂直平板表面的波数分量，kx为空气中垂直平板表面的波数分量，ε′和μ′分别为介质板的相对介电常数及相对磁导率.通过对比这两个体系的反射系数和透射系数的内在联系，引导学生探讨其中的Fab ry-Perot共振机制，如图3（b）所示.此外，可以进一步引导学生思考在光密到光疏介质环境下，入射波超过其临界角入射时，一定会出现全反射吗？是否存在奇异的电磁材料能够打破常规认识：超过临界角时，甚至可以无反射波？引导学生分析介质平行板的反射系数，可以发现存在电磁参数复共轭且纯虚的超构材料可以实现超过其临界角时，不会出现全反射现象［6］，并在其满足一定阻抗条件下实现无反射的电磁场衰减或电磁场放大效应.图3（c）和（d）是CO MSOL的模拟场图（颜色分布表示空间电／磁场分布，黑色箭头表示能流分布，入射波的振幅为1），完美验证了理论结果：在超构材料电磁参数为ε=0.5i，μ=-0.5i（有效折射率为0.5）且入射角度为39.2°时，TE入射波是实现无反射的电磁场放大效应，而TM 入射波实现了无反射的电磁场衰减效应［6］.此外，该结构体系还具有其他的新奇物理现象值得师生共同探讨其中的物理机制.

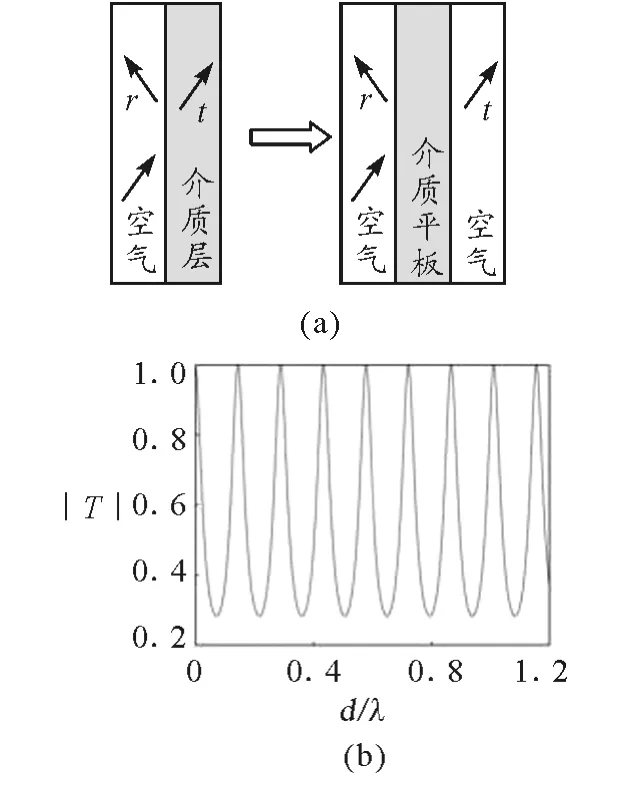
图3 电介质平行板的Fab ry-Perot共振现象和基于超构材料的无反射电磁场放大／衰减效应

3.2 二维金属平行板波导

在电磁波传播的教学内容中，矩形波导中的电磁模式传播问题相对比较复杂，如图4（a）所示，通过分离变量等手段求出电磁波导中的特征传播常数

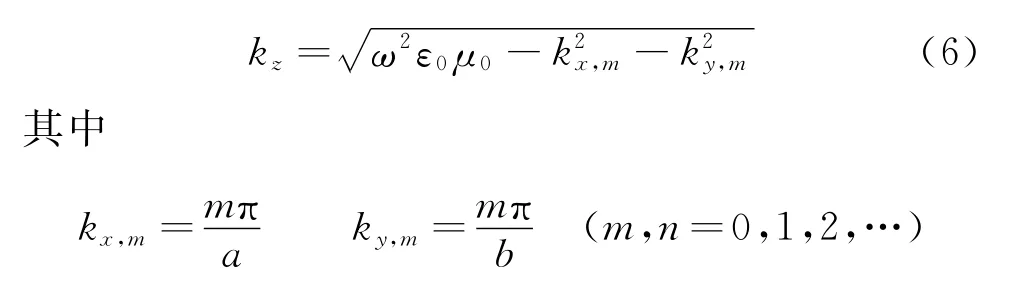
很多教材会在列出截止频率后，指明三维波导中TE波模式的基模为TE01或TE10模.对于TM波而言，m及n则都不可为零.当x或y方向波导宽度为无限大时，可以启发学生研究金属平行板波导［如图4（b）所示］的电磁模式传播问题，该情况下的波导传播常数

图4（c）是通过M ATLAB列出的不同波导模式的传播常数与波数的对应关系，可以发现TE波与TM 波的差异仅在于是否存在零模，也就是说TE波的基模为TE1，而T M 波无截止频率，其基模为TM0（对应自由空间的TEM模式）.这些结果在CO MSOL的仿真实验能够得到证实.从图4（d）中我们能发现，当我们取图4（c）中总波数为6.28时，TE0模不存在，TM0模能够被激发.对于TM1或TE1模式来说，两种偏振波都能够被激发.而对于TM2或TE2模式，两种偏振波是倏逝波，在波导中发生了迅速的衰减而无法传播.通过CO MSOL数值仿真，学生能够清晰地观察到不同波导模式的传播情况，增加了对课本三维矩形波导传播规律的深入理解.该二维金属平行板波导还可以与其他材料结构相结合，引导学生学习不同的物理机制探索一些奇特的波导光学现象.比如，在二维金属平行板波导中间引入渐变折射率电介质材料，通过波导模式演化机制，实现多样化的波导功能器件［7］.

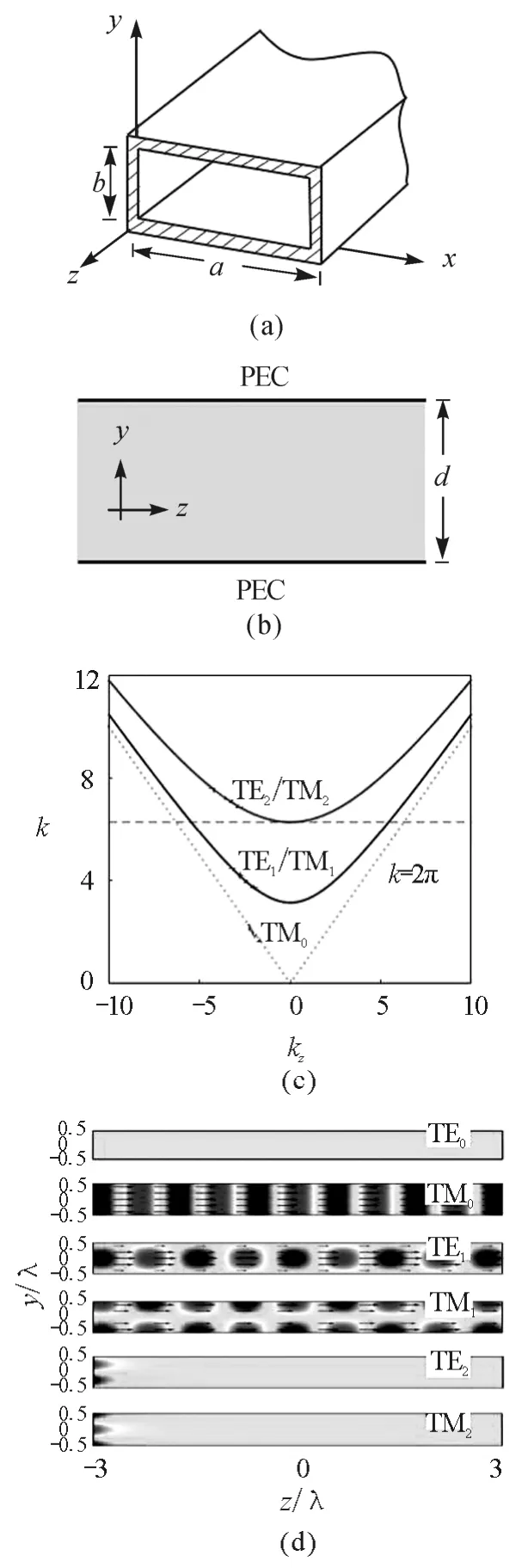
图4 二维金属平行板波导传播模式和模拟场图

4 结束语

笔者关于前沿研究融入电动力学课程教学的探索和实践，并通过以上的实例展示，我们可以发现，前沿研究可以让电动力学的基础教学内容得到拓展和延伸.科研软件的使用可以让教学具有生动性，帮助学生理解抽象的理论知识.依照类似的方法和思路，其他前沿研究成果也可以巧妙地融入到电动力学的基础教学中去［8］.需要注意的是，针对不同学校的学生能力、水平的差异，相关前沿成果的选择难度要因地制宜，同时要保证一定的阶梯性，能够让不同层次的学生都能参与其中，实现不同的发展目标.比如，能力较差的学生可以通过仿真实例的趣味性、操作自由等特点调动他们的学习兴趣，巩固基础知识；能力较强的学生可以在挑战学科前沿知识的过程中锻炼其思维方式、发明创新等能力，能够形成一定的自主科研能力.前沿研究与电动力学教学结合的案例值得有关高校教师进一步探索，使具有悠久历史的电动力学课程不断添加科技发展的新鲜血液，让电动力学的课程教学能够实现经典和前沿、基础和创新、理论和实际的紧密结合，满足新时代下基础学科人才培养的需求.