刍议在高中数学教学中化归思想渗透的教学策略

张威

摘 要：数学是一门培养学生逻辑思维能力的理论基础课程，数学思想是数学解题的灵魂，而在诸多数学思想方法中，化归思想是一种重要的解题思想，更是一种有效的数学思维方式。广大高中数学教师为更有效提升教学质量，在每一节课堂上充分渗透化归思想，旨在达成教学成果更为显著的提升。本文针对高中数学教学中化归思想渗透的教学策略进行以下讨论。

关键词：高中数学;化归思想;教学策略

数学是一个人们学习中非常基础的学科，它是科学发展的基础，同时也是支持着各行各业发展的基础。随我国社会发展，各行业的求才若渴，高中数学教师们有意识将学生思维能力培养作为高中数学教学基本目标之一，旨在提升学生分析问题能力和解决问题能力，为社会培养具有数学思维的高级人才。

1.化归思想在高中数学教学中的重要意义

化归的基本功能是：将生疏转化成熟悉，将复杂转化成简单，将抽象转化成直观，将含糊转化成明朗。简单来说，化归思想的实质就是将运动变化发展的观点、事物之间的相互联系，以相互制约的观点去看待问题，善于将想要解决的问题进行转化思考，最终得以解决[1]。这也是辩证唯物主义的基本观点。把复杂的内容简化处理，它的另一层含义就是化整为零。

高中所用的数学教材内容多是遵循由易及难、由浅至深的理念，也就是说，后面的学习需要使用前面的知识进行铺垫。化归思想是数学基础思想之一，回归本源的思想是教好数学的前提，因此，在高中教学课堂上，教师将新的数学知识转化为旧的数学知识，在这基础上进行教学。化归思想潜移默化深入到学生脑海之中，促进了学生将数学知识进行转化的思想逐渐形成，提升学习理解能力和解题能力，从而提升学生学习成绩。

2.化归思想应遵循的基本原则

2.1熟悉化原则;即将新接触的数学问题转化为我们熟悉的问题，以我们熟悉的知识和解题经验来解决问题。

2.2简单化原则;复杂的问题简单化是最有效解决问题的方法，通常通过对简单问题的解决，逐步深化至复杂问题，不仅可以达到解题的目的，还可以获得新的启示或解题依据，促使数学思维得到新的拓展。

2.3和谐化原则;将数学中知识中遇到的问题或理论，使用符合数与形所表示出的和谐形式，将其推演出符合人们数学思维规律的解题方法。

2.4直观化原则;即将抽化的、不可见的问题转化为直观可见的形式后再进行演算。

2.5反难则反原则;当正面讨论不能解的难题时，就可以通过反面思考进行探求，从而使难题获得解决。

3、高中数学教学中化归思想渗透的教学策略

化归思想并不难体会，简而言之就是转化和归结的意思，即将复杂的问题、陌生的问题通过转化和归结的思想，将问题转化到简单、熟悉的问题上来。化归思想在高中数学中应用非常广泛。笔者根据自身经验进行以下实践总结[2]。

3.1由未知到已知，進行化归思想渗透

由未知到已知的教学策略是不断寻求一个将所要解决问题的充分条件，将需要解决的问题转化为已知知识条件下进行问题解决的方法。

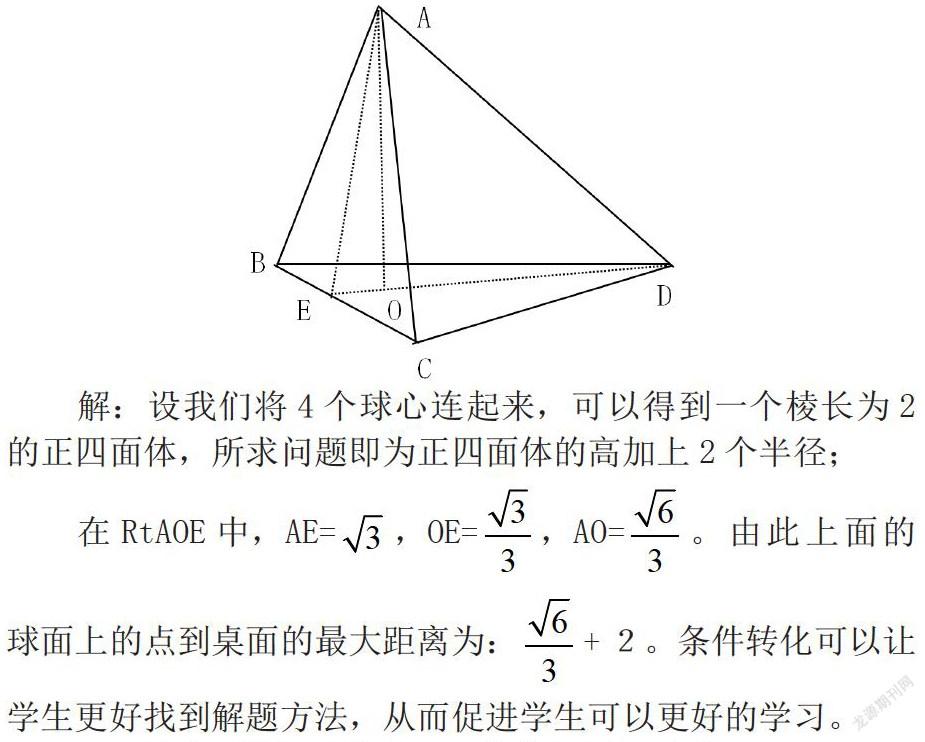
例如;将已知的4个半径为1的球，两两相切放在桌面，下面3个，上面1个。求上面球面上的店到桌面的最大距离。

解：设我们将4个球心连起来，可以得到一个棱长为2的正四面体，所求问题即为正四面体的高加上2个半径;

3.2通过理清数量关系，深化化归思想渗透

理清数量关系对学生对数学知识的理解非常重要，所以，在数学教学过程中，引导学生理清数量关系也是教学关键之一。而在理清数量关系的基础上，再去渗透化归思想，可以使学生解题更加容易。通常高中阶段的学生，学分两极化非常严重，而大多在数学学习中出现障碍或困惑的学生，主要还是因为他们未能有效掌握数学思想，从而使得自身学习受到了限制，所以教师还需耐心引导学生将数量关系先理清楚，再逐步渗透化归思想。

3.3挖掘隐性信息，实现数与形的转化

有些学生在进行数学解题时一直找不到突破口，是因为数学题目中往往都蕴藏着隐性信息，教师在教学课堂上需将这些信息有效的挖掘出来，并针对其隐藏性对学生加以引导。有些时候，只有将这些信息充分的挖掘出来，才能有助于实现数与形的真正转化。特别是在高中几何教学中，教师需要充分挖掘影藏信息，激发学生数学思维，有效实现化归思想的运用。

例如;设直线过点P（x，y）分别与x轴的正半轴和y轴的正半轴相交于A、B两点，该过程点Q与点P关于y轴对称，O为坐标原点BP=2PA，且OQ·AB=1。求P点轨迹方程。

类似以上数学题目解析，挖掘出其中的隐性信息后采用化归思想，将难题转化为简单且熟悉形式进行解答，将繁复的数量关系转为简单化。通过挖掘、研究、联系并解决相关问题，从而使得数学题目得到全面解决。

3.4总结解题策略，延伸化归思想

数学需要不断的进行总结、反思，学习才能得到更多的全面提升。所以教师需引导学生将所学的数学知识不断的进行解题策略上的总结和探求，以求数学思想可以得到延伸[3]。通常来说，可以构建一个学习小组，每小组平日可以进行新题、错题、有新思路的题进行解锁和探讨，在小组得不到有效解题方法时也可以找老师进行共同探讨。通过这个过程，学生数学思维会得到有效激化，同时会得到有效应用，从而使得化归思想成为直接、有效的解题途径。

例如：已知椭圆的两个焦点是F1（0，-2），F2（0，2，离心率e=，问椭圆方程，并是否存在直线L与椭圆交于不同点M、N，且线段MN恰被直线x=-平分？若存在，求出L的倾斜角的范围。第一小题较为容易解：椭圆方程易得：y2/9+x2=1。而针对第二小题，学生可能会想出的解题方法是：假设直线存在，设立出方程，联立椭圆方程，组成一个方程组，再根据判别式求出k的取值范围，从而得出倾斜角范围。那我们是否可以通过参数方程，转化成三角函数来解答呢，事实证明是可以行的。在总结解题策略时化归思维的运用在一定条件下是可以拓宽解题方法的，化归思维的有效运用可以在增强学生理解能力的同时，提升学生数学思维能力。

3.5整体化策略，夯实化归思想运用

教学实践表明，有意识的放大考察问题“视角”，需将题目看做是一个整体，通过研究其整体结构、整体形式（在此过程中注意已知条件及待求结论在其中的地位和作用），通过整体结构的调节、扩展及转化使题目获解[4]。这种从整体结构考虑，整体观点出发研究问题的思维活动被称为整体思维。

4.化归思想应用要规范

4.1条件转换要全面;在进行数学解题过程中，条件梳理与转化是解题关键，在进行转化时一定要充分考虑条件，挖掘其隐藏性，针对其全面性，切忌顾此失彼造成的转换不等价。

4.2思路要灵活;数学解题过程就是一个由条件进行结论等价转换的过程，但是在其转化过程并不是唯一性的，因此在进行数学解题时，需要从实际条件出发，灵活转换，从不同的角度去思考和解决问题。

结束语：总而言之，化归思想是一个教师在教学过程中通过多途径、多方式、多方法的反复渗透，引导学生善于发现问题、思考问题并解答问题的全过程。化归思想的有效运用可以使高中学生在学习中将遇到的数学难题，使用原始化、简单化的方式解答出来，是具有重要意义的方法和理念。

参考文献

[1] 吴进.化归思想在高中数学教学中的应用[J].中学数学，2018，（1）：75-77.

[2] 孙丹.巧妙转化灵活变通——从”化归法”专题习题课说起[J].中学数学，2018，（13）：88-90.

[3] 雷自学.递推数列通项公式的求法[J].中学课程辅导（教学研究），2018，12（29）：194-195.

[4] 鲁子扬.化归思想在高中数学解题过程中的应用[J].中华少年，2018（22）：129-129.