谈复习课堂教学中计算能力的有效提升
张树斌

摘 要:计算能力的提升是初中数学教学的重要目标之一,这项目标的锁定与实施需要教师从多个角度、多个环节去落实.就数学课堂教学行为而言,我们要结合很多种课型进行开展.笔者就复习课堂教学中的计算能力提升谈几点拙见.
关键词:计算能力;复习课;勾股定理;多元
中图分类号:G632文献标识码:A文章编号:1008-0333(2020)17-0003-02
勾股定理在初中数学的教学过程中是一个难点和重点,学生不仅需要知道勾股定理的来龙去脉,更需要熟练应用勾股定理解决实际应用类问题,此时对学生的计算能力和思维能力都提出了较高的要求.笔者结合勾股定理知识点总结复习一课,就相应环节如何达成计算能力的提升做以下阐述.
一、多元拼图证明,让计算服务证明
证明勾股定理是我们在学习勾股定理的一个必要过程,这个证明的方法和路径有很多种,而我们在课堂中,需要引领学生用一种方法多个策略去证明勾股定理,一方面通过学生的熟练精准的计算来提升学生的计算能力,另一方面是让学生在多元证明的过程中,体验计算的巧妙性、科学性、严谨性,也让学生深刻感受到计算的重要性和必要性.比如,我们让学生通过两种方法拼图和计算来完成以下证明:
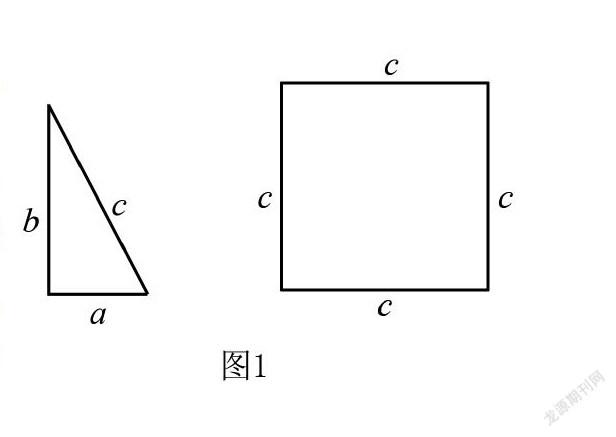
例题1 如图1所示,用硬纸板做成的四个全等的直角三角形(两直角边长分别是a,b,斜边长为c)和一个边长为c的正方形,请你将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的图形的示意图;
(2)利用该图形证明勾股定理.
方法1:拼成如图2所示的图形,此时我们可以结合大正方形面积减去四个小的直角三角形的面积等于小正方形的面积,从而列出表达式:4×12ab+(b-a)2=c2,从而推出勾股定理表达式.
方法2:拼图拼成如图3所示的图形,此时我们同样可以结合大正方形面积减去四个小的直角三角形的面积等于小正方形的面积,从而列出表达式:c2+4×12ab=(a+b)2,从而推出勾股定理表达式.
在这个过程中,学生的计算能力得到有效的训练,而训练的效果就是巧妙地证明了勾股定理.
二、熟悉主要应用,让计算对接应用
数学是一门工具性很强的学科,而计算则是数学学习中的主要工具,可想而知,数学计算成为工具中的工具,核心中的核心,因此,计算一定离不开应用,离不开实战性的训练.为此,在勾股定理的复习过程中,我们在应用环节还是渗透了计算的任务给学生,以任务驱动生长.
1.求边的问题.我们通过勾股定理可以解决“已知直角三角形的两边求第三边”的问题,在问题的启发下,我们建构如上表格,让学生很快建构出“已知直角三角形的两边求第三边”的方法,学生的口算计算和应用能力火速提升.在完成表格后,我们进行一定的运算,以此提升学生的计算熟练程度,训练学生的计算能力.随之,我们再次提问学生,如果“已知直角三角形的一邊与另两边的关系,求直角三角形的另两边.”如下:
例题2 若一个直角三角形的一条直角边长是7cm,另一条直角边比斜边短1cm,则斜边的长是cm.
学生在实实在在的计算和训练中,归纳总结出这个方法.对比前面两种方法,学生不难发现,解决这类问题的一般方法,即已知直角三角形的一边及两边之间的关系,就可以求出第三边.这里就要充分考虑学生对勾股定理应用的熟练程度和学生的计算能力.学生在深入的计算过程中,深刻感受到计算的重要性和必要性.从意识形态上提升了学生对计算题的重视程度.
2.求证平方关系.在初中数学中,很多线段之间存在一种平方的关系,面对这种问题,我们可以借助勾股定理来得以突破,为了让学生深刻感受到这种应用的价值性和实用性,我们还是可以让学生通过计算来达成.这种达成让学生再次感悟计算的重要性,其中计算能力的有的放矢的训练也为学生验证“利用勾股定理可以证明线段平方关系的问题”这一应用的实用性.
例题3 如图4,已知△ABC中,∠ACB=90°,以△ABC的各边为边在△ABC外作三个正方形,S1、S2、S3分别表示这三个正方形的面积,S1=6,S3=25,则S2=.
这类计算让学生明显发现其中巧妙利用勾股定理的计算,结合线段的平方关系而解出答案.学生在解答的过程中,将正方题中面积中的平方关系和勾股定理中的平方关系巧妙融合在一起,在亲自的计算体验中,也积累了这种基本的计算技能.
3.求作n的线段.初中数学的计算,在很大程度上是和图象、线段、作图紧密相关的,这种关系也再次凸显了数学计算的应用之广,也充分凸显了数学的学科魅力和价值.对此,我们需要进一步引导学生在本节复习课中去寻找这层关系,而教师结合具体问题的引导与思考是教学策略的首选.比如,我们需要让学生在数轴上画出表示 13及-10的点.在没有学习勾股定理前,这样点是很难准确地画在数轴上的,但是学好勾股定理以后,我们可以发现13是边长为3和2的直角三角形的斜边,为此,我们只需要构建一个直角三角形即可.同样,-10也可以同样画出来,此时在思考的过程中,对学生的口算、心算的计算能力要求较高,学生看到13和-10以后,要结合勾股定理很快锁定相应的直角三角形和直角边的长度,具体解法如图5所示.
在此,我们充分还原学生计算的机会,让学生在教师的引导下,深入计算训练.计算不仅解决问题,还收获结论,充分提升了学生参与计算训练的兴趣与信心,也促进学生计算能力的可持续提升.
虽然学生参与计算的过程是枯燥乏味的,但是教师在教学过程中,充分结合教学内容的特点,抓住其内在魅力,用科学合理的问题设计,激励学生的参与,我们将收获很多,此时,学生将会兴趣倍增,我们的教学效果也是事半功倍.
参考文献:
[1]张建芬.如何建构富有新意的初中数学复习课[J].中学数学,2019(12):5-6.
[2]薛霞燕,易良斌.基于“教、学、评”一致性的复习课设计——以“二次根式”为例[J].中学数学教学参考,2019(09):2-5.
[责任编辑:李 璟]

