巧用隐圆模型 突破思维壁垒

仇书芹

摘 要：在中考数学试题中，我们经常会遇到一类有关圆的题目，这类题目在条件中没有直接给出圆的有关信息，需要我们分析和探索，挖掘出这些隐藏的圆（简称隐形圆），再利用和圆有关的知识进行求解，由此深感对此类问题通性通法研究的必要性.

关键词：几何;模型;隐形圆

中图分类号：G632文献标识码：A文章编号：1008-0333（2020）17-0029-03

一、根据圆的定义发现隐形圆

圆在几何中的定义是：平面内到定点的距离等于定长的所有点组成的图形叫做圆.定点称为圆心，定长称为半径.当题目中的条件出现“定长”、“定点”这些条件时，可考虑作出隐形圆来解题.

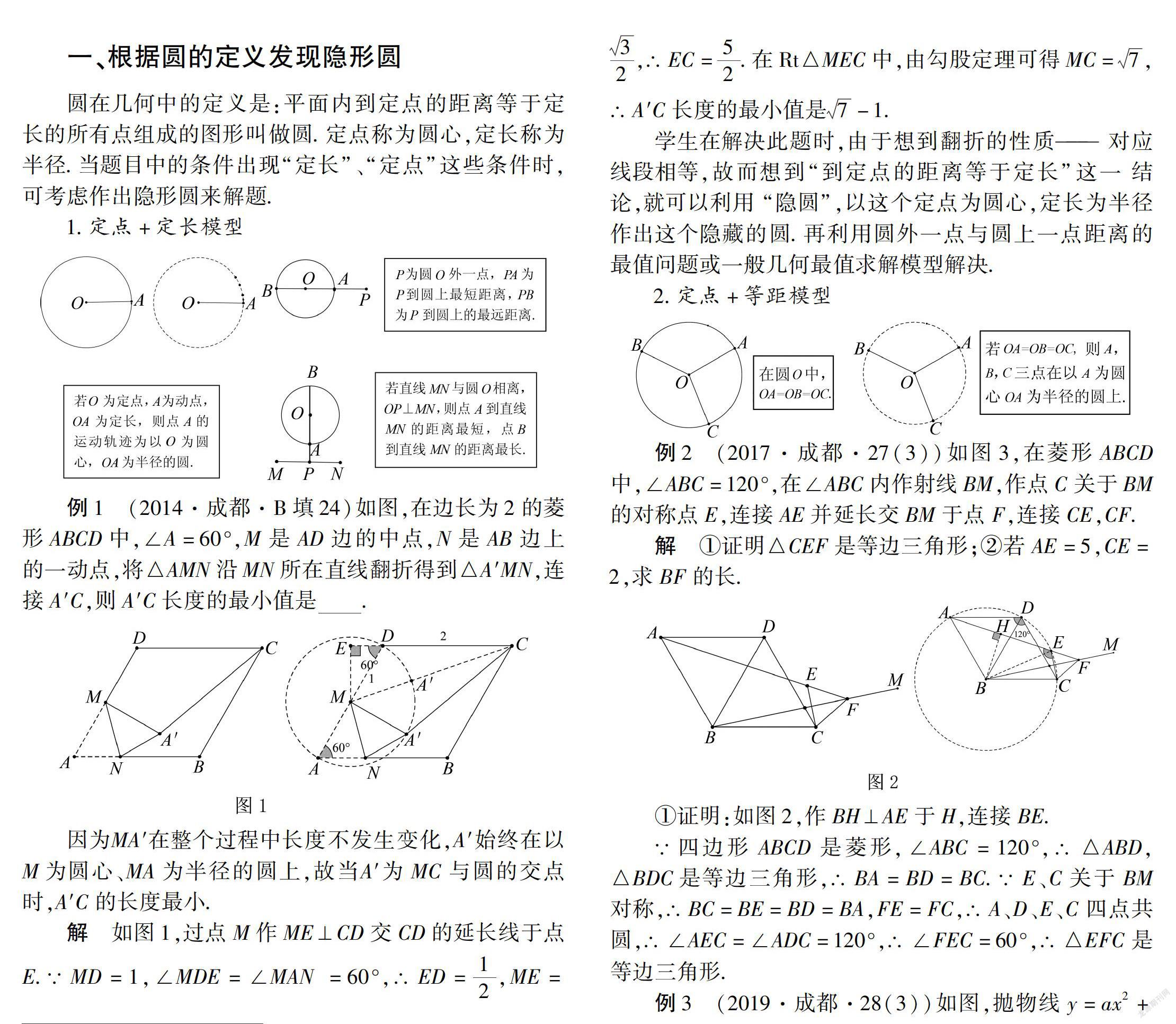
1.定点+定长模型

例1 （2014·成都·B填24）如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是.

因为MA′在整个过程中长度不发生变化，A′始终在以M为圆心、MA为半径的圆上，故当A′为MC与圆的交点时，A′C的长度最小.

解 如图1，过点M作ME⊥CD交CD的延长线于点E.∵MD=1，∠MDE=∠MAN =60°，∴ED=12，ME=32，

∴EC=52.在Rt△MEC中，由勾股定理可得MC=7，∴A′C长度的最小值是7-1.

学生在解决此题时，由于想到翻折的性质—— 对应线段相等，故而想到“到定点的距离等于定长”这一 结论，就可以利用 “隐圆”，以这个定点为圆心，定长为半径作出这个隐藏的圆.再利用圆外一点与圆上一点距离的最值问题或一般几何最值求解模型解决.

2.定点+等距模型

例2 （2017·成都·27（3））如图3，在菱形ABCD中，∠ABC=120°，在∠ABC内作射线BM，作点C关于BM的对称点E，连接AE并延长交BM于点F，连接CE，CF.

解 ①证明△CEF是等边三角形;②若AE=5，CE=2，求BF的长.

①证明：如图2，作BH⊥AE于H，连接BE.

∵四边形ABCD是菱形，∠ABC=120°，∴△ABD，△BDC是等边三角形，

∴BA=BD=BC.∵E、C关于BM对称，

∴BC=BE=BD=BA，FE=FC，∴A、D、E、C四点共圆，

∴∠AEC=∠ADC=120°，∴∠FEC=60°，∴△EFC是等边三角形.

例3 （2019·成都·28（3））如图，抛物线y=ax2+bx+c经过点A（-2，5），与x轴相交于B（-1，0），C（3，0）两点.

（1）求抛物线的函数表达式;

（2）点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC′D，若點C′恰好落在抛物线的对称轴上，求点C′和点D的坐标;

（3）设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当△CPQ为等边三角形时，求直线BP的函数表达式.

解 （3）①如图3，当点P在x轴的上方时，点Q在x轴上方.

∵∠C′BH=60°，由翻折得∠DBH=12∠C′BH=30°.

∵点Q在抛物线的对称轴上，∴QB=QC.

∵△CPQ为等边三角形， ∴QP=QC，∴QB=QP=QC，

∴B、C、P在以Q为圆心QC为半径的圆上.

∴∠PBC=12∠PQC=30°，∴∠PBC=∠DBH，

∴点D在直线BP上.∵B（-1，0），D（1，233），

∴直线BP的函数表达式为y=33x+33.

②如图4，当点P在x轴的下方时，点Q在x轴下方.

同理可得∠PBC=12∠PQC=30°.

设BP与y轴相交于点E，

在Rt△BOE中，OE=OB·tan∠CBP=OB·tan30°=33，

∴点E的坐标为（0，-33），

∴直线BP的函数表达式为y=-33x-33.

综上所述，直线BP的函数表达式为

y=33x+33或y=-33x-33.

从以上例题我们可以看出，当题目的条件中出现一个定点，并能找到到这个定点的距离等于定长的一些点时，就可以根据圆的定义作出隐形圆.

二、根据定线对定角发现隐形圆

圆中的任意一条弦长确定，则所对的圆周角也确定.当题目中出现定长的线段及所对张角为定角时，可考虑作隐形圆解题.1.定弦+直角模型

例4 （2018·成都·28（3））如图，在平面直角坐标系xOy中，以直线x=52对称轴的抛物线y=ax2+bx+c与直线l：y=kx+m（k>0）交于A（1，1），B两点，与y轴交于C（0，5），直线l与y轴交于点D.

（3）若在x轴上有且仅有一点P，使∠APB=90°，求k的值.

解 如图5，由题可得：k+m=1，∴m=1-k.

∴直线l：y=kx+1-k，∴kx+1-k=x2-5x+5，

即x2-k+5x+k+4=0.

∴x1=1，x2=k+4.

∴B（k+4，k2+3k+1）.

设AB的中点为Q，∵点P有且只有一个，∠APB=90°，

∴点P在以 AB为直径的圆上，以 AB为直径的圆与

x轴只有一个交点P，且为切点.

∴QP⊥x轴，∴P为MN的中点.

∴ xp=xM+xN2=1+k+42=k+52，∴P（k+52，0）.

∵△AMP∽△PNB，∴AMPM=PNBN， ∴AM×BN=PN×PM.

∴1×k2+3k+1）=k+4-k+52（k+52-1），

即3k2+6k-5=0，解得k=-1±263.

∵k>0，∴k=-1+263.

2.定弦+非直角模型

例5 （2019·鄂尔多斯·16）如图，在圆心角为90°的扇形OAB中，OB=2，P为AB上任意一点，过点P作PE⊥OB于点E，设M为△OPE的内心，当点P从点A运动到点B时，则内心M所经过的路径长为.

解 如图6，∵PE⊥OB，∴∠PEO=90°.

∵点M是内心，∴∠OMP=135°.

∵OB=OP，∠MOB=∠MOP，OM=OM，

∴△OMB≌△OMP（SAS），

∴∠OMB=∠OMP=135°，

∴點M的轨迹是弓形OB上的圆弧，

∴OB所在圆的圆心Q一定在弦OB的中垂线上，

且∠BQO=2（180°-135°）=90°.

以OB为斜边在OB的左边作等腰Rt△QOB，

以Q为圆心，OB为半径作圆.

∴点M的轨迹是OB，其所对的圆心角∠BQO=90°，

∴内心M所经过的路径长90π×2180=2π2.

三、根据定弦对等角或互补发现隐形圆模型

当位于线段异侧的两个角互补或位于线段同侧的两个角相等，则这四个顶点在同一个圆上，即四点共圆.

例6 （2017·重庆·24（2））如图，△ABC中，∠ACB=90°，AC=BC，点E是AC上一点，连接BE.

（1）若AB=42，BE=5，求AE的长;

（2）点D是线段BE延长线上一点，过点A作AF⊥BD于点F，连接CD、CF，当AF=DF时，求证：DC=BC.

（2）如图7，∵∠ACB=90°，AC=BC，∴∠CAB=45°.

∵AF⊥BD，∴∠AFB=∠ACB=90°，

∴A，F，C，B四点共圆，∴∠CFB=∠CAB=45°，

∴∠DFC=∠AFC=135°.

在△ACF与△DCF中，AF=DF，∠AFC=∠DFC，CF=CF，

∴△ACF≌△DCF（SAS），∴CD=AC.

∵AC=BC，∴DC=BC.

例7 （2019·张家界·14）14.如图：正方形ABCD的边长为1，点E，F分别为BC，CD边的中点，连接AE，BF交于点P，连接PD，则tan∠APD= .

解 如图8，连接AF.

∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE.

易证Rt△ABE≌Rt△BCF（SAS），则有AE⊥BF，∠APF=∠ADF=90°.

∴A、P、F、D四点共圆，∴∠AFD=∠APD.

∴tan∠APD=tan∠AFD=2.

“隐形圆模型”的应用实际上是数学建模的其中一种形式，《数学课程标准》指出，数学教学要让学生亲自经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等方面得到进步和发展.

因此要提高学生解决几何问题的能力，在平时的教学过程中，我们教师要善于引导学生将所学内容整理归纳出类型和方法，经过加工提炼，得出有指导价值、有典型结构的数学模型，培养学生识别模型、应用模型的能力，能在有限的考试时间内，快速破解难题.

参考文献：

[1]沈萍华.道是无“缘”却有“圆”——构造隐形圆解题的几种思路[J].初中数学教与学，2018：59-60.

[2]曹晓荣.构造辅助圆解题的思路与方法[J].初中数学教与学，2019：20-22.

[3]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[责任编辑：李 璟]