“无中生有”巧思维,三角函数妙求解

◇ 山东 万 刚

在三角函数的化简、运算、求值、证明恒等式等问题中,经常会“无中生有”——构造常数、相应的参数、特殊平面图形、平面向量等,进而结合三角函数、平面几何、平面向量等知识,灵活运用三角基本公式进行求解,往往可以使问题的解决更为有效、快捷.

1 无中生“1”

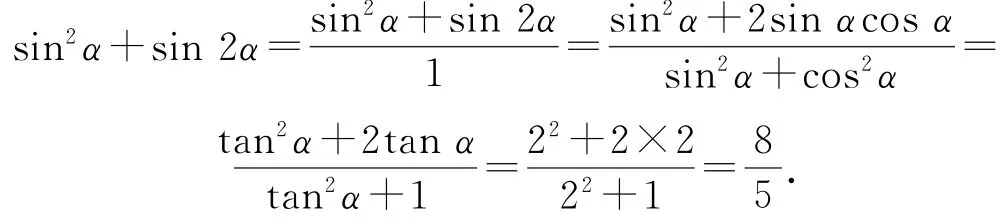
2 无中生“参”

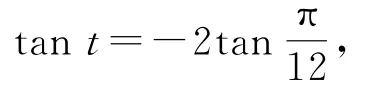
则

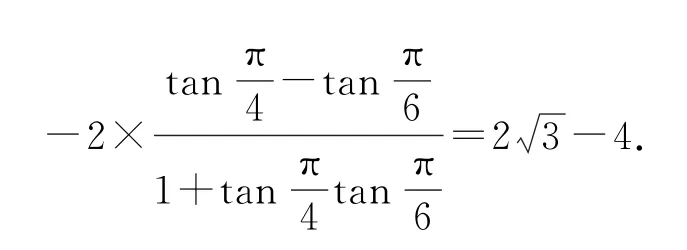
3 无中生“图”

画出y＝sin2x,x∈[－3,3]的图象,如图1 所示,再由sin2x＞0,易得,故所求函数的定义域为

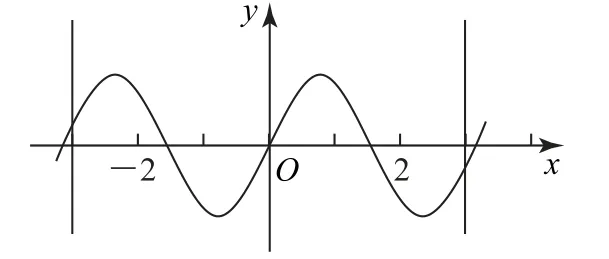
图1

4 无中生“向量”

所以f(x)＝2cosx＋sinx 的最大值为5.

5 无中生“等式”

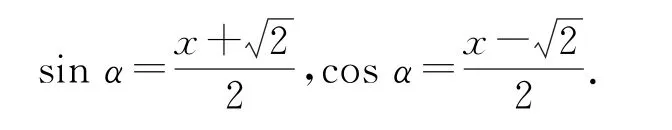
于是,根据sin2α＋cos2α＝1,可得,解得x＝0,即sinα＋cosα＝0,所以sinα＝－cosα.故所求

6 无中生“导数”

cosθ＝－2sinθ.

于是,结合sin2θ＋cos2θ＝1,解得

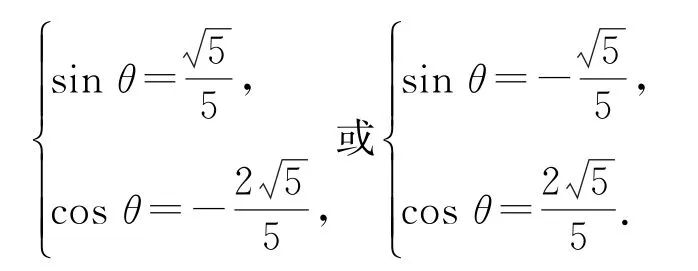
经检验知：前者满足f(x)取得最大值,后者满足f(x)取得最小值.故所求

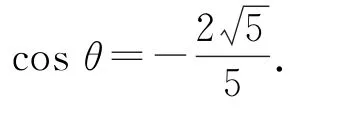
要想真正做到“无中生有”,必须做到“胸有成竹”.平时必须熟练掌握三角函数及其相关知识,多练习,多揣摩,就能不断达到“无中生有”,融会贯通,提升自己的数学素养,提高自己的解题能力.