阀控非对称液压缸数学模型及建模方法研究

李晓园， 陈炘， 叶鹏， 李鑫， 徐祥， 蒋辉， 李琼柱

(红塔烟草(集团)有限责任公司 玉溪卷烟厂,云南 玉溪653100)

0 引 言

液压控制系统的种类及分类方法很多，根据液压放大器与执行元件的不同组合，可分成阀控缸、阀控马达、泵控缸、泵控马达4种[1-2]，其中阀控缸响应快、精度高、应用最广。目前实际使用中的伺服阀，主阀部分多以四通滑阀为主，这是一种结构对称的阀，进油侧和回油侧的结构参数完全相同[3-5]。当信号大小不变，仅改变极性时，阀芯运动方向改变，只变换了执行元件的进出油口，伺服阀两侧的系统及控制参数并没有变化。若采用双杆活塞油缸（又称为对称油缸），则执行元件也是对称的，此时的执行元件只是运动方向发生了变化，其余速度推力等基本参数和未换向前一样。由于这种结构对称导致的控制对称、力学及运动学参数对称，给应用带来了极大的方便，使得对称阀及对称缸的组合形式在相当长的一段时间内居于统治地位[6]。

单杆活塞油缸只有一边有活塞杆，两腔面积不等，所以又称为非对称液压缸。与双杆油缸相比，结构简单、泄漏部位少，同等行程的条件下外形尺寸小，对于一些大型设备或外形尺寸受限的场合有明显的优势。近年来，阀控非对称缸应用逐渐增多，但所使用的阀仍然是对称的。相对系统而言，这就使得系统的整体对称性受到了破坏，执行元件在两个方向上的力学运动参数都发生了变化[7-11]。要想双向都具有满意的控制性能，必须对依据对称特点建立的数学模型及控制策略都做出相应的改变。多年研究积累至今，已产生了许多种阀控非对称缸的数学模型[12-15]。这些模型因研究者着眼点、简化方法不同，从形式到内涵都有一定的差异，根据数学模型得出的伺服系统分析设计、结论也必然不同，这就给以阀控缸为动力元件的液压伺服系统设计使用带来不便，为此对各种阀控非对称缸的数学模型的特点及适用范围作一个讨论是很有必要的。

1 现有阀控非对称缸数学模型及建模方法分析

1.1 基本方程

目前数学建模一般采用分别建立伺服阀和液压缸的基本方程，再加以化简的方式完成。阀控非对称缸无杆腔进油的计算简图如图1所示，基本方程有3类，共5个方程式。

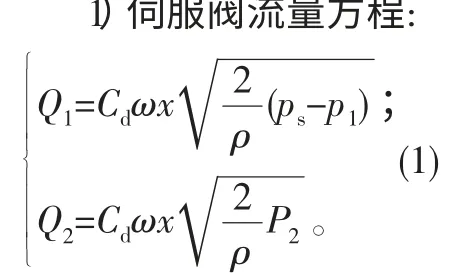
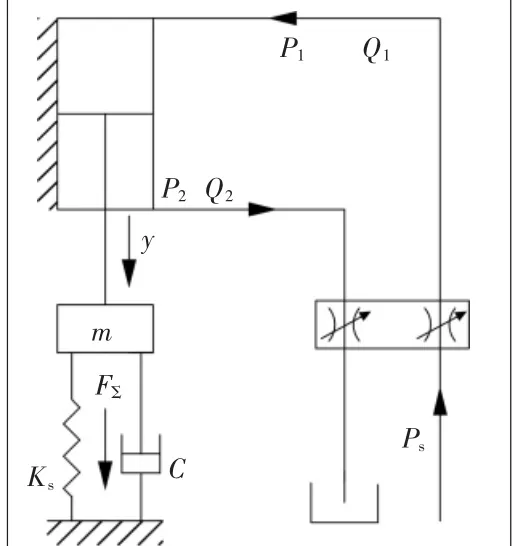
图1 无杆腔进油计算简图

2）油缸连续方程：

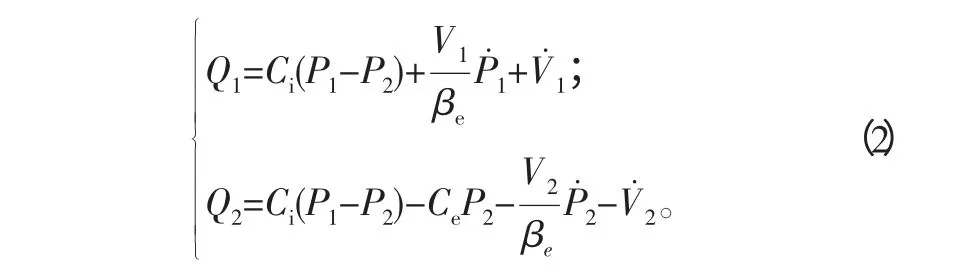
3）油缸力平衡方程：

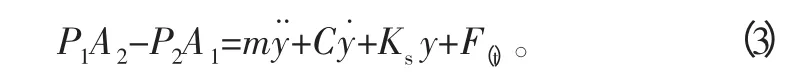
式中：V1为油缸无杆腔有效容积，m3；V2为油缸有杆腔有效容积，m3；P1为油缸无干腔压力，Pa；P2为油缸有杆腔压力，Pa；A1为油缸无杆腔面积，m2；A2为油缸有杆腔面积，m2；Ce为油缸外泄漏系数，m5/N·s；Ci为油缸内泄漏系数，m5/N·s；Ps为油泵供油压力，Pa；y为油缸活塞杆的位移，m；x为伺服阀阀芯的位移，m；F（t）为等效总外负载，N；Cd为伺服阀流量系数；ω为伺服阀主阀阀芯面积梯度，m；C为等效黏性阻尼系数，N·s/m；βe为油液等效体积弹性模量，Pa；M为运动部件总质量，kg；Ks为等效负载弹簧刚度，N/m；ρ为油液密度；V˙1=A1y˙；V˙2=A2y˙。

式（1）～式（3）即为阀控非对称缸无杆腔进油时的基本方程。

1.2 数学模型

线性化取增量式，作拉氏变换后消去中间变量Q1、Q2、P1、P2并简化，理论上就能得出以x为输入、FΣ为干扰、y为输出的较精确的传递函数模型。但这样所得的传递函数非常复杂，实际上无法进行有效分析并得出有价值的结论。为此，现有数学模型都是对上述基本方程作了各种简化处理后得出的。常用的方法是仿照阀控对称缸的处理方式，引入负载压力PL、负载流量QL及静态条件下的连续方程进行简化。PL、QL定义不同就可得出不同的辅助方程，由此得到不同的传递函数模型，常见的有以下3种。

1）取辅助方程为：

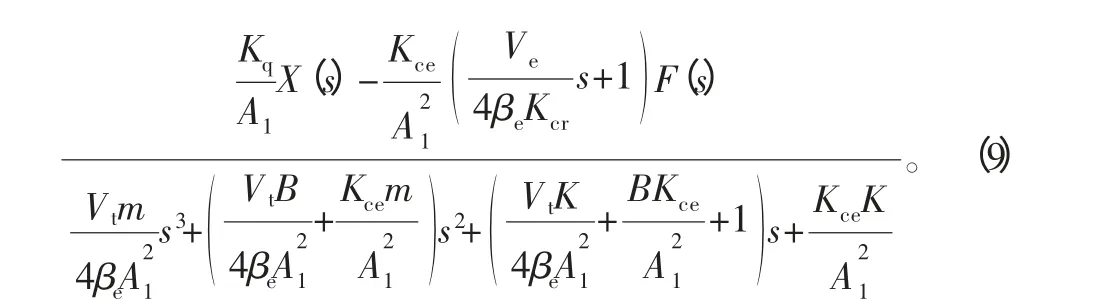
以上3种辅助方程所得出式（5）、式（7）、式（9）所示的传递函数模型，式中各系数的组成及意义，请参考其各自的源文献，此处不再一一说明。

以上3种方法的区别主要在于辅助方程的选取，比较各方法，可发现辅助方程的差别是由于对PL、QL的定义及表达不同引起的，现将我们对于上述方程的认识讨论如下供大家参考：

1）QL的定义。相对于活塞运动所需的流量而言，缸的泄漏量与液容效应可产生的流量很小，若是对称油缸忽略此二项后，可得

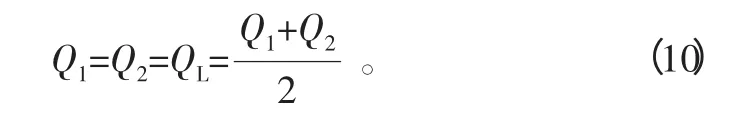
此时的QL可以视为Q1、Q2的稳态近似值，应该是合理且无可非议的。但是对于非对称液压缸来说，任何时候Q1都不可能等于Q2，在此定义下，系统中已找不到与之对应的实际流量，由此带来定义上的偏差是不可避免的，故QL的上述这种定义对于非对称液压缸不适用。

2）PL的定义。若为对称油缸则：A1=A2，令FΣ=my¨+By˙+Ky+f（t）称为总负载，令：则此时式（3）仍然成立，负载关系的定义也不变，而PL=P1-P2，已找不到与FΣ之间的简单对应关系了。显然对于非对称液压缸来说，PL只能采用式（13）的定义。

3）文献[3]分析了PL、QL的定义，从功率平衡的角度证明了QL=(Q1+Q2)/2及PL=P1-P2的定义是不可能的，在输入输出功率平衡的基础上提出采用QL=Q1；PL=P1-nP2作为辅助方程，这里Q1是油缸进油腔流量，显然这种定义方式避免了本节第1）段中所述QL的缺陷，更为合理。

4）静态方程的引入。以上3种简化方法都引用下式：

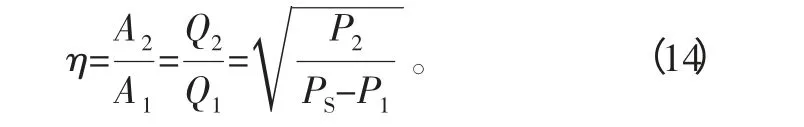
此方程后一半是从式（1）直接得出的精确表达式，前一半则是在忽略液容效应及泄漏量后根据静态连续方程得出的。考虑实际使用中作为伺服系统中可用的油缸泄漏极小，液容效应产生的流量与油缸运动所需流量相比很小，作此简化产生的误差是可以接受的，这也是迄今为止，各种模型简化都无一例外采用的原因。考查式（5）、式（7）、式（9）可以发现，3种简化方法所得到的模型非常接近，但由于辅助变量选取的不同，所得模型的准确程度是有差别的，根据前面对辅助方程的讨论，以方法（3）的假设更为合理，可信度理应最高。

2 精确建模方法

从现有的简化方法可以看到辅助变量PL、QL只是作为运算用的中间变量，在最终结果中并不出现，预先设置PL、QL并非绝对必要。相反PL、QL的定义不当或不准确，还可能产生额外的误差。若能抛弃这一不必要的环节，保留较简单、合理的静态方程为辅助方程，其余直接由基本方程出发，应该能够得出更为精确的数学模型。考虑到非对称液压缸双向的差异，两个运动方向的进油情况并不相同，强行将两个运动方向的数学模型统一用一个方程表达并不可取，两种进油方式对应的数学模型应分别考虑。

2.1 无杆腔进油

如图1所示，阀控非对称缸无杆腔进油，此时的静态连续方程为

从式（20）消去Q1（s）、P1(s)、P2(s) 后可得阀控非对称缸无杆腔进油时的传递函数模型为

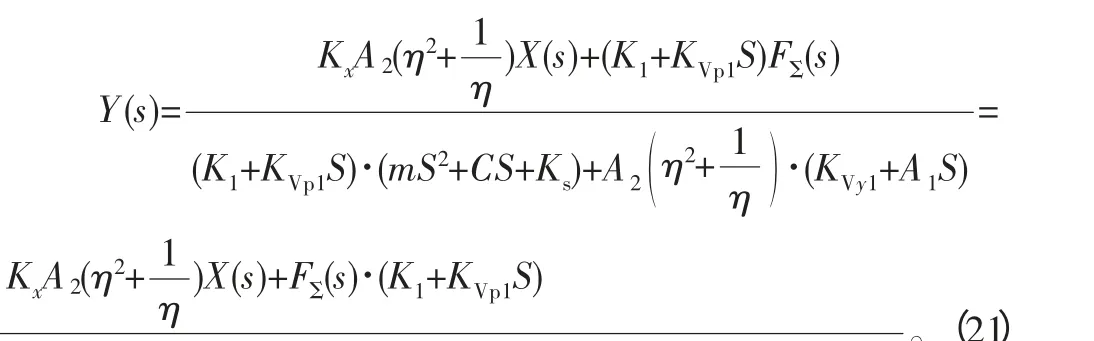
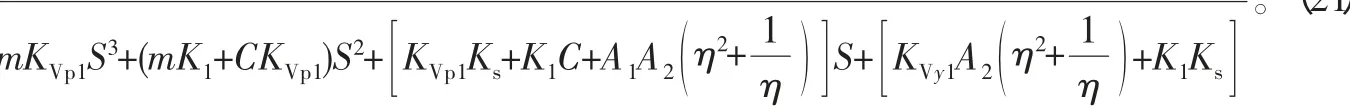
式中：

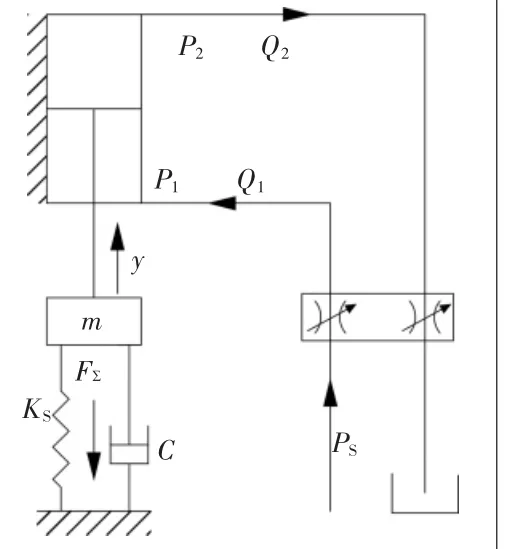
图2 有杆腔进油计算简图

2.2 有杆腔进油

阀控非对称缸有杆腔进油的计算简图如图2所示，此时的静态连续方程为

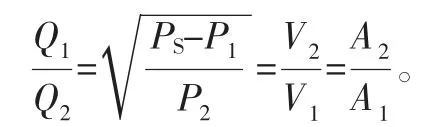
化简后可得

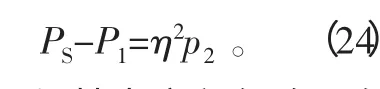
与基本方程组合可得简化的有杆腔进油时非线性模型为：

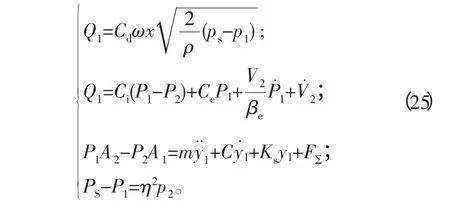
将式（25）线性化取增量式，可得有杆腔进油时的线性化增量数学模型为：

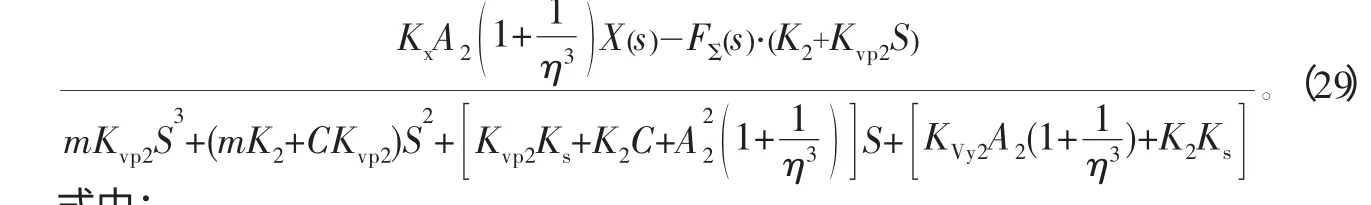
对比式（23）、式（31）两式，二者结构、阶次完全相同，但系数有很大差别，说明非对称油缸两个方向上的控制性能是不一样的，必须分别建模，区别处理。

3 结 语

1）非对称油缸的基本方程一定，中间变量的选取对最终数学模型的形式和精度有重大影响。2）非对称油缸结构的不对称，导致两个方向控制参数的不对称，其数学模型也是不一样的，应该分别建模，区别处理。3）若承认非对称油缸控制的不对称，分别建模，习惯上的中间变量并非必不可少，完全可以不出现而直接建模。