一种弯管管道机器人驱动模块关键结构设计及其运动仿真
裴文超, 张平宽, 张宇尧, 李登超
(太原科技大学 机械工程学院,太原030024)
0 引 言
管道运输目前是运输天然气、工业生活用水及石油等介质的主要工具,居于相当重要的地位,涉及到工业生产和人民生活的各个方面,尤其是金属管道的运输。而在管道的运输中,根据运输路径的变化或结构要求,常会出现弯管部分,因此管道运输是直管和弯管的结合。金属管道的腐蚀破裂会带来难以想象的危险,若天然气、石油输送管道发生爆炸、泄漏危害人们的生命和生态环境的平衡,并且带来一定的经济损失[1]。尤其是城市地下布置的金属管道,不仅容易被腐蚀,而且因为其处于地下深埋环境,对于管道维修也有相当的难度[2]。因此,对于使用中被腐蚀的小管径金属管道进行管内检测、除锈和修补等工作,值得关注而且迫在眉睫。本文中提出的是一种适用于小管径弯管机器人的驱动模块,该种弯管机器人可以在φ90~φ110 mm的小管径里面进行检测、修补、除锈等作业工作,而驱动模块的设计使用,不仅可以使得弯管机器人有更长的作业距离、更高的工作效率,又能使得机器人模块化设计更加完整。本文主要结合理论推导、计算得出该驱动模块关键结构参数同弯管直径、曲率的数值关系,运用此数值关系设计驱动模块并验证其在弯管中的通过性。该项研究为整个弯管机器人模块设计提供参数化设计条件,可以更方便、快捷地设计出适合不同管径的弯管机器人系列产品。
1 驱动机构简介
如图1所示,该种小管径弯管机器人驱动模块分为3部分,两端分别为前、后支撑部分,中间为联结传导部分。驱动模块的工作原理是:通过电动机带动直线凸轮旋转,直线凸轮将圆周运动变为直线运动,带动连杆、滑块、支撑脚,使得驱动模块间歇性地支撑弯管内壁,实现机构的蠕动运动,而棘爪-棘轮结构控制机构整体的前进后退。由柔软并且可以伸缩的波纹管连接前后机架,防止相对转动。依靠对直线凸轮的设计,实现前后支撑、传动的同步性,使得驱动机构平稳地进行蠕动运动,达到驱使整个弯管机器人向前或向后运动的目的。

图1 驱动模块
2 模块结构参数与管道尺寸数值关系
2.1 弯管的选择
根据材质、尺寸等类别,管材被划分为多种多样的规格,《管材和管件选用手册》可以作为选择常用管材的设计依托和验证工具。本次选择的是铸铁管,管径D为100 mm、曲率半径R为76 mm的U形弯管,此弯管的材质和曲率半径在工业生产和居民日常生活中比较常见。选择此种管材型号进行驱动模块的设计验证,可以保证驱动模块的通用性,同时也验证了驱动模块在曲率半径小、弯曲角度大的情况下,可以顺利工作。
2.2 驱动模块长度与通过性关系
为使得弯管机器人驱动模块顺利平稳地通过一定尺寸条件的弯管,其长度应该满足如下条件:因为要使得弯管机器人能够通过弯管,其每一部分都要满足弯管对于长度数值的限制条件。通过分析计算得出限制驱动模块通过弯管需要满足的长度条件为:

式中:R为弯管曲率半径;D为弯管的直径;α为弯管弯曲角度,U形管的弯曲角度为180°;L为驱动模块各单元总长;dmax为模块的直径,为70 mm;Lmax表示在一定几何尺寸的弯管和模块直径dmax的条件下,驱动模块单元能通过弯管的最大长度。
根据推导的数值关系与选择的弯管尺寸标准,得出机构的总长上限为119.24 mm。此弯管机器人驱动模块设计的总长为108 mm, 驱动模块中支撑模块和传动模块的长度分别为35 mm和30 mm,三者均小于能通过弯管的长度极限值。因此,符合机构通过弯管的结构数值关系,该机构在几何关系的约束下,可以顺利通过弯管。
2.3 驱动模块蠕动步长同弯管参数的关系
该弯管机器人是一种以蠕动的方式运动的新颖结构。蠕动式驱动对于蠕动步长有一定的要求,步长过长会导致机构的卡死,且不易实现机构运动的连续性,步长过小,对于机器人前进、后退及作业效果有一定的影响。通过结构的分析,推导出弯管曲率、弯管管径同驱动模块蠕动步长的数值关系,以设计和验证驱动模块运动的可行性与稳定性。

图2 通过性结构分析
当该驱动模块通过180°的U形弯管时,因为机构中的零部件为刚性体,支撑脚具有一定的自适应性,在转弯的过程中,两端的支撑中心会始终固定在弯管中心线上,而中间轴部分会随着角度和蠕动运动的变化,致使整体机构长度变化,而相对于中心线发生一定的偏转。因此简化分析,根据图2所表示的参数,得出蠕动步长同弯管直径、弯管曲率之间在结构上的数值关系为:

式中:D为管道直径;R为弯管曲率半径;Lmax为驱动模块连接传导部分的最大长度;L1为驱动模块压缩后连接传导部分的最小长度;ΔL为蠕动步距;d为驱动模块最大直径。
结合模块结构的设计和上述2.1节中推导出来的可通过弯管的机构最大长度,可以得出蠕动步长同弯管直径、弯管曲率半径的数值关系,该数值关系可应用到弯管机器人驱动模块的设计和验证部分。
2.4 驱动模块支撑脚的设计同弯管参数的关系
本次设计的弯管机器人驱动模块,其支撑方法是利用在圆周上等角度分布的3个支撑脚对管壁施加力的作用。因为转弯过程中该驱动模块机构姿态会随着管道弯曲的角度而发生一定的变化,所以整个机构会有倾倒的可能性。一旦驱动模块支撑部分发生倾倒,在模块未识别而继续运行的情况下,极有可能会在管道中卡死,导致电动机功率过高而损坏,甚至有损坏机器人、堵死管道的可能。为此,需要对该驱动模块进行防倾倒的设计。该驱动模块防倾倒的设计,运用结构尺寸对触角进行结构封闭,从而使其在结构上没有倾倒的可能性,以保证整个机器人的顺利工作运动。
如图3(a)所示,机构收缩的时候,管径和模块支撑脚直径之间有空隙,是最有可能发生倾倒的时候。因此,若支撑脚发生倾倒的临界瞬间,对角方向上的尺寸大于管径,倾倒便不会发生,而且会随着支撑脚以后的支撑运动而自动地随着支撑脚边缘的弧度将驱动模块姿态调整回来。因此,简化分析后,得出数值关系(如图3(b)):

式中:d1为支撑脚收缩后的直径;L2为支撑脚轴向长度;D为管道直径。

图3 防侧倾结构分析
结合此数值关系,可以设计出来在结构尺寸上防止机构倾倒的支撑脚的轴向尺寸和支撑机构收缩的最小尺寸。
3 ADAMS仿真分析
3.1 导入模型
因为在ADAMS软件中创建模型工作量较大,而且也更容易出错,所以在保证其主要结构的前提下,选择SolidWorks软件创建本驱动模块易于进行ADAMS软件分析的三维模型,并将其保存为.X_T文件格式,后导入ADAMS中进行通过性仿真分析。主要有以下4部分工作:1)设置单位为MMKS制,设置重力为默认,为每个零部件添加材料属性为steel;2)为驱动模块需要有相对运动的位置添加运动副,以保证其按照设定的运动原理进行工作;3)通过ADAMS软件的冲激函数法,计算支撑脚同管壁的接触刚度和弹簧的弹性模量等参数并设置;4)在模型树中检查导入模型属性及添加的运动副和弹簧的属性,确认无误的情况下,打开Tool—Model Verify以检查模型是否有过度约束等情况。
3.2 仿真与分析
设置好各部分参数和约束后,进行仿真运算,其仿真过程如图4所示。

图4 驱动模块管内姿态
由图4可以看出,在驱动模块进入弯管、在弯管中部、退出弯管等3种状态下,均未发生干涉。再由图5和图6分析可得,驱动模块前后驱动部分,路径连续并且基本保持一致,速度也基本保持一致,说明整体机构运动具有统一性,并未发生卡顿的现象,该驱动模块可以顺利通过此曲率半径的U形弯管。
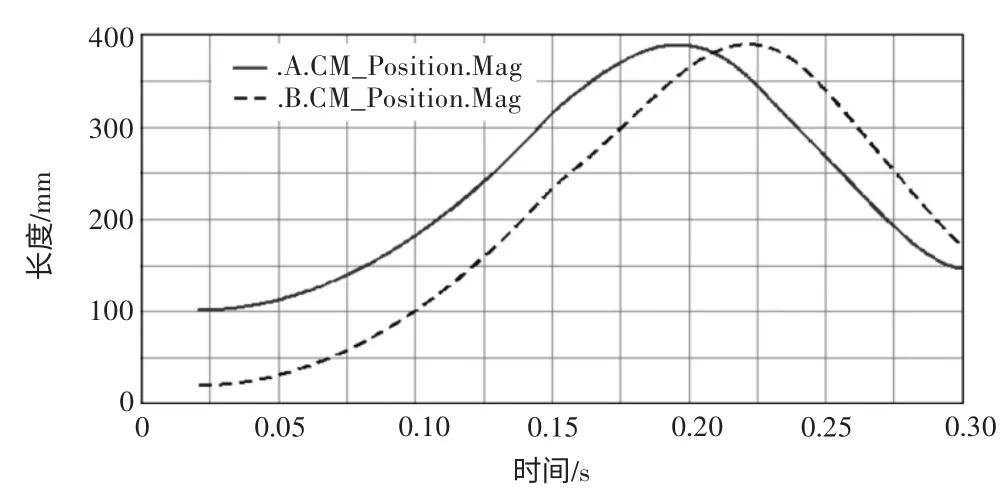
图5 前、后支撑路径分析图

图6 前、后支撑速度分析图

图7 前支撑脚速度分析图
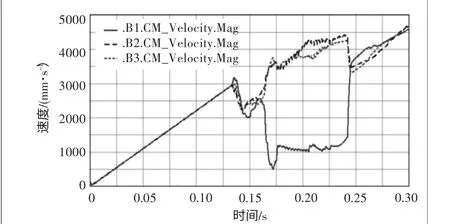
图8 后支撑脚速度分析图
由图7和图8分析可得,模块前后分布的驱动支撑脚A1、A2、A3和B1、B2、B3,其速度曲线基本保持一致,发生偏差的主要原因为:驱动模块需要增加整体机构稳定性,使得前后支撑端的支撑脚错位布置,导致ADAMS软件在仿真过程中由于空间位置的不同而使得测算的速度也不同。整体曲线变化趋势基本保持一致,可得出该驱动模块可以保持整体运动的稳定性。
4 结 语
综合上述分析可得:1)本次设计的弯管机器人驱动模块,其参数是根据本文中依照结构分析计算得出驱动模块参数同弯管直径、曲率半径和弯曲角度的数值关系求得的。通过SolidWorks软件和ADAMS软件的建模、仿真、分析,确定了该驱动模块在生活、工业中常用的管径为φ100 mm、曲率半径为76 mm的U形管材的可通过性,也代表了其在更小弯曲角度的弯管中的可通过性。2)通过实例证明了数值关系的正确性,为后续的弯管机器人驱动模块自动化设计奠定了一定的基础,是弯管机器人自动化设计的一部分。

