土结构接触界面的宏细观参数敏感性分析

王桂萱, 鞠碧玉, 秦建敏

(大连大学土木工程技术研究与开发中心, 辽宁 大连 116622)

土-结构的接触界面是关乎整个工程安全的重要部位．由于土与结构两种材料的性质差异较大, 且接触界面的性质既不同于土体也不同于结构, 导致土-结构接触界面研究难度较大．目前国内外学者针对接触界面的研究主要通过物理试验和数值模拟两种手段．李永辉等[1]针对桩-土界面进行了剪切试验研究, 发现随剪切位移的增大, 界面剪切应力达到极限值后出现软化现象; Li等[2]根据振动台试验结果, 采用三维有限元数值模拟, 分析了土-结构在地震激励下的相互作用, 证明接触压力、应变幅值等随激振增大而增大．物理试验主要从宏观上研究接触界面的力学行为, 结果真实可靠, 但对实验仪器精度要求较高, 且造价较高; 而离散元法(distinct element method, DEM)作为研究颗粒材料力学行为的方法已被普遍认可[3]．Jing和Zhou等[4-6]采用离散元法分析颗粒形状、粗糙度和荷载参数等土-结构界面性质, 解释了土-结构界面的微观机制; 但是目前采用离散元法针对土与结构接触界面的研究较少, 且分析因素单一．本文拟从接触界面内部结构出发, 采用离散元法建立二维接触界面模型[7], 对颗粒间摩擦因数、孔隙比、颗粒形状、法向应力以及刚度比等参数进行敏感性分析, 探讨颗粒材料的宏微观力学响应, 为接触界面的材料优化和改性提供理论参考．

1 离散元计算模型

1.1 孔隙胞元体系

基于孔隙胞元的离散元法[8], 将颗粒体试样看作由n个孔隙胞元构成, 图1为孔隙胞元示意图, 其中σ11、σ22分别为法向与切向应力．以每个颗粒的几何中心为顶点, 顶点间的连线代表相互接触颗粒间的连接,连线构成的多边形空间称为孔隙胞元．通过相互接触颗粒间的相对运动计算每个孔隙胞元的变形．

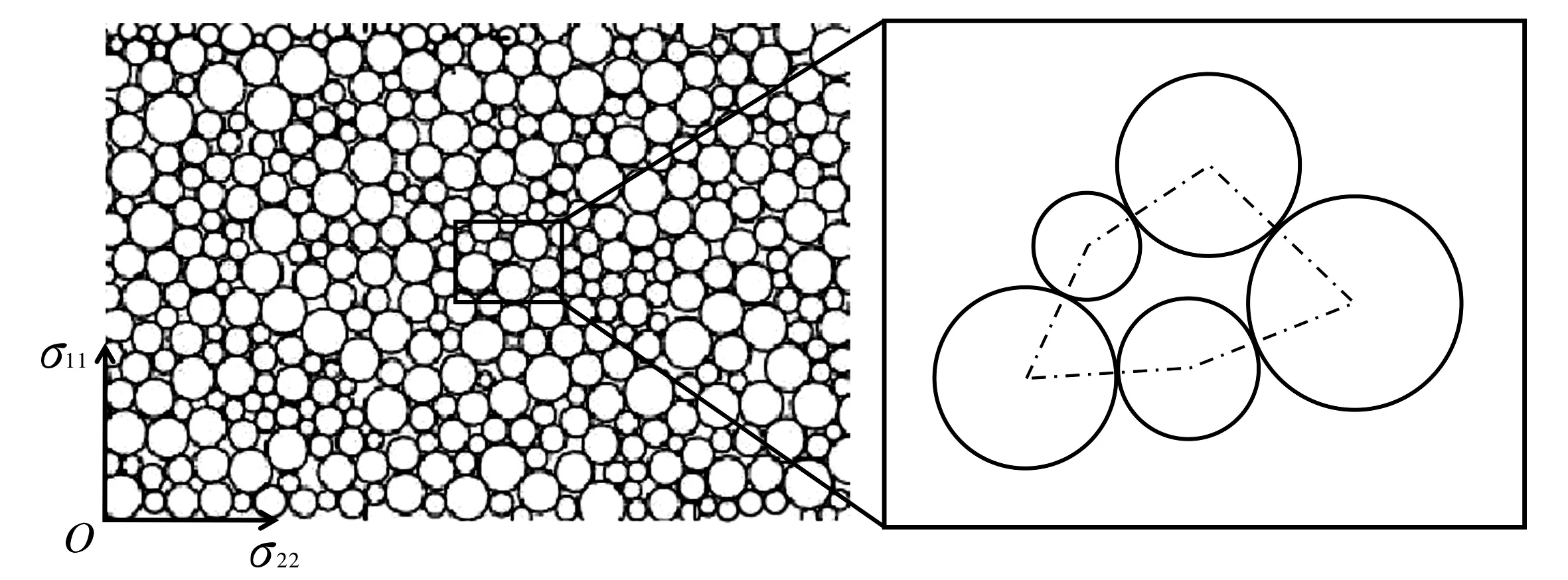
图1 二维孔隙胞元结构Fig.1 Two-dimensional void cell structure

1.2 颗粒体试样

采用圆形颗粒与简单的线弹性接触模型生成二维颗粒试样, 不考虑粒间胶结作用,颗粒在边界范围内随机排列, 颗粒体试样为长60 mm、高15 mm的长方形, 颗粒个数为1 000个, 中值粒径D50=1.1 mm, 颗粒粒径为0.5D50～1.5D50随机分布, 不均匀系数Cu=1.69．试样的初始孔隙比e=0.154, 初始状态为紧密、随机、各向同性排列, 颗粒的初始重叠量为1.01×10-2D50．颗粒重度为20 kN·m-3, 法向刚度kn=2.5×108N·m-1, 刚度比ks/kn为0.25, 颗粒间摩擦因数μ=0.5(摩擦角26.57°)．

1.3 边界条件

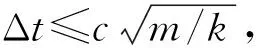
1.4 模型验证

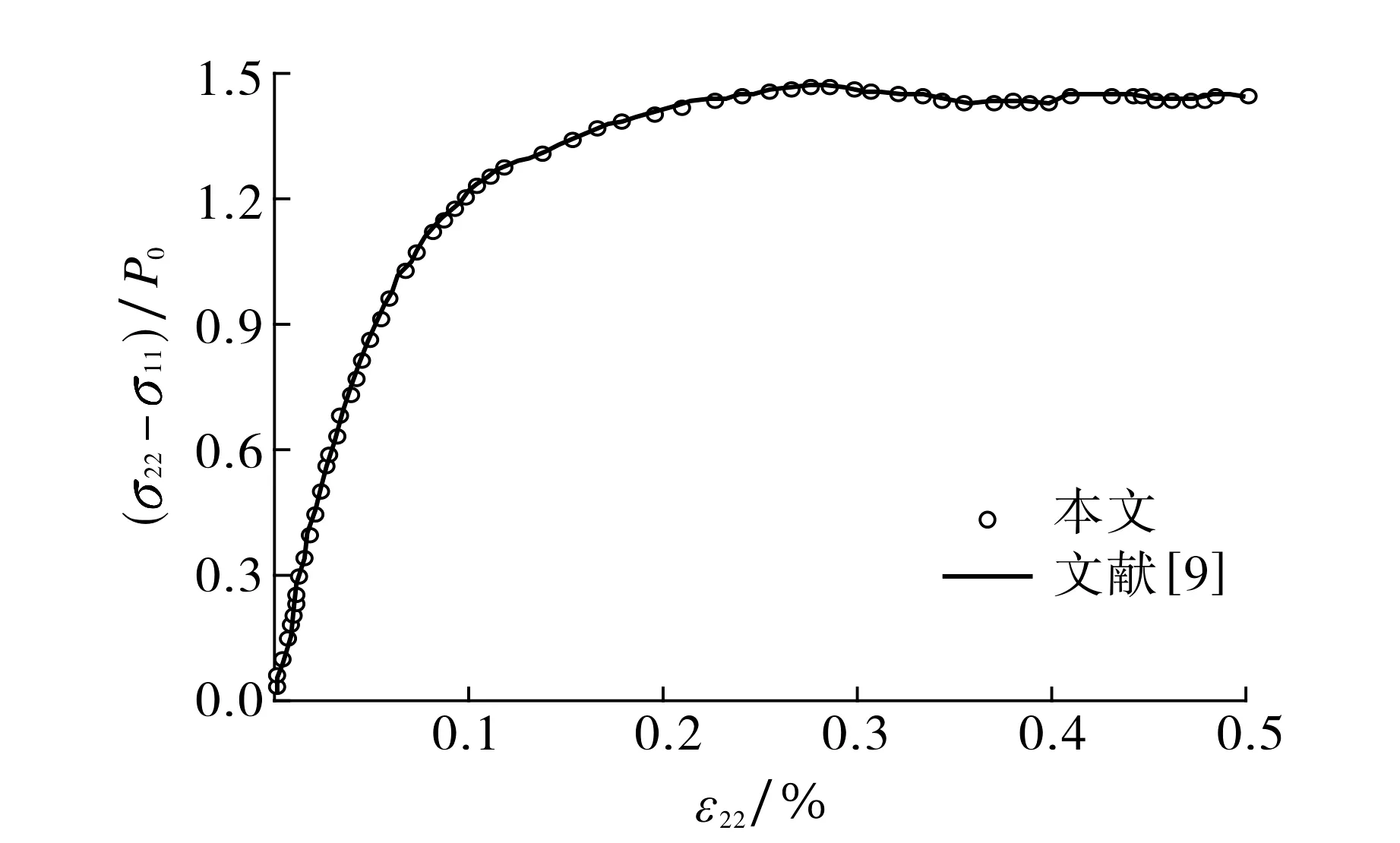
图2 应力-应变关系曲线Fig.2 Stress-strain relationship curves

为了验证二维离散元程序的准确性, 采用离散元程序建立与文献[9]相同的试样模型, 由4 008个颗粒组成的二维颗粒体,材料参数取值与文献相同,接触刚度为常数, 对比结果如图2所示, 其中P0为初始围压,ε22为切向应变．从图2可以看出, 本文计算结果与文献结果基本一致, 验证了二维离散元程序计算结果的可靠性．

2 细观参数分析

2.1 摩擦因数

控制其他物理力学参数不变, 选取μ为0.1～0.9的颗粒体进行对比分析, 得出不同摩擦因数下颗粒体接触界面应力比(σ22/σ11)应变和应力比峰值((σ22/σ11)max)关系曲线, 如图3所示．由图3(a)可见, 当摩擦因数较小时, 应力比基本无峰值, 硬化后无明显软化现象, 此时应力比-应变关系接近理想弹塑性关系; 当摩擦因数较大时, 颗粒体在加载初期的力学性能接近弹性,随着加载的进行, 应力比达到峰值后进入软化阶段, 最后达到平稳的临界状态．软化现象的产生是由于颗粒间存在咬合力, 剪切过程中咬合力不断遭到破坏,导致颗粒体的强度降低．随着摩擦因数的不断增大, 硬化速度逐渐提高, 初始弹性模量逐渐增大, 软化现象也越来越明显．由图3(b)可见, 随着摩擦因数的增大,应力比峰值也逐渐增大,根据最小二乘法拟合结果得出,应力比峰值与摩擦因数成正比,摩擦因数影响土体抗剪强度,摩擦因数越大,颗粒间咬合作用越明显,颗粒体抗剪强度越大．综上所述, 颗粒间摩擦因数对颗粒体的宏细观力学行为具有较大影响．

图3 不同摩擦因数的颗粒体应力比-应变曲线和应力比峰值Fig.3 Stress ratio-strain curve and stress ratio peak of particles with different friction factor

图4为2个不同摩擦因数时法向和切向接触力(颗粒间相接触产生的力)对应力比的贡献．由图4可见, 不同摩擦因数时, 法向接触力均占主导地位,而切向接触力对总应力的贡献均较小; 但随着摩擦因数的增大, 切向接触力的贡献比重有所提高, 但仍远低于法向接触力的贡献值．

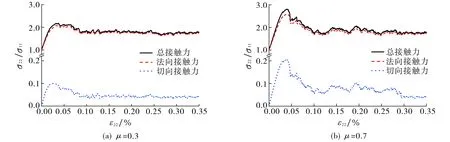
图4 不同摩擦因数时法向、切向接触力对应力比的贡献Fig.4 The contribution of the normal and tangential contact force to the shear stress under different friction factor

图5给出了不同摩擦因数下孔隙比和配位数Nc随切向应变的变化曲线．由图5(a)可见, 加载初期不同摩擦因数下的孔隙比均有所下降, 且随着切向应变的增加逐渐增大, 并趋于稳定．初始孔隙比较小时不存在明显峰值, 当初始孔隙比逐渐增大时,孔隙比峰值和临界值均随之增大．由此可知,剪切过程中颗粒体先经历压实阶段,土体出现剪缩现象;随颗粒间咬合作用的逐渐破坏,颗粒发生滑动、翻转等运动, 土体由剪缩变为剪胀; 随摩擦因数的不断增大,土体剪缩和剪胀现象也逐渐明显．综上所述, 颗粒间摩擦因数对土体剪胀性具有较大影响．由图5(b)可见, 不同摩擦因数颗粒体的初始配位数基本相同,加载初期配位数有所降低, 随后逐渐增大,后期达到平稳状态;摩擦因数较大颗粒体的配位数大于摩擦因数较小颗粒体, 表明接触界面的宏观力学性质受微观配位数的影响．

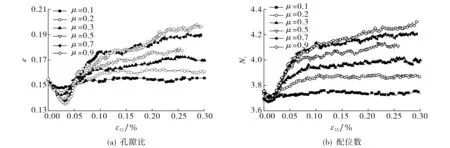
图5 不同摩擦因数的孔隙比和配位数与应变的关系曲线Fig.5 Void ratio-strain and coordination number-normal strain curves with different friction factor

图6 弹性模量、泊松比及摩擦角、剪切模量与摩擦因数的关系曲线Fig.6 Relationship curve of elastic modulus, Poisson’s ratio, friction angle, shear modulus and friction factor

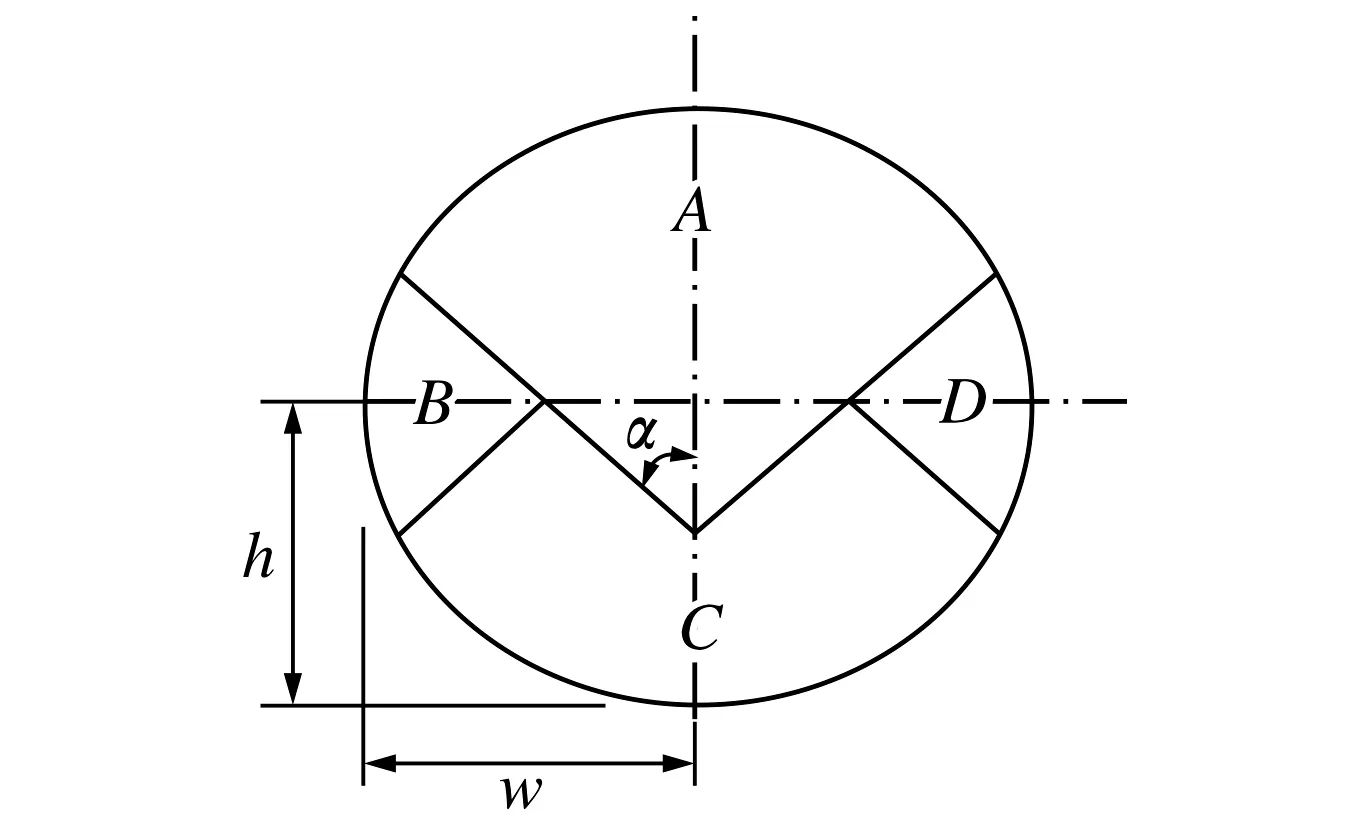
图7 组合圆弧颗粒Fig.7 The combined arc particle

2.2 颗粒形状

表1 颗粒体初始参数

图8给出了二维颗粒体形状分别为圆形和组合圆弧的应力比、孔隙比、配位数随切向应变的变化曲线．由图8(a)可见, 组合圆弧颗粒的应力比和初始弹性模量均高于圆形颗粒,归因于组合圆弧颗粒间的咬合作用较强; 由图8(b)可见,组合圆弧颗粒的受剪膨胀性比圆形颗粒高; 由图8(c)可见,组合圆弧颗粒的配位数大于圆形颗粒,除加载的初始状态外,单个组合圆弧颗粒比单个圆形颗粒的接触数大．

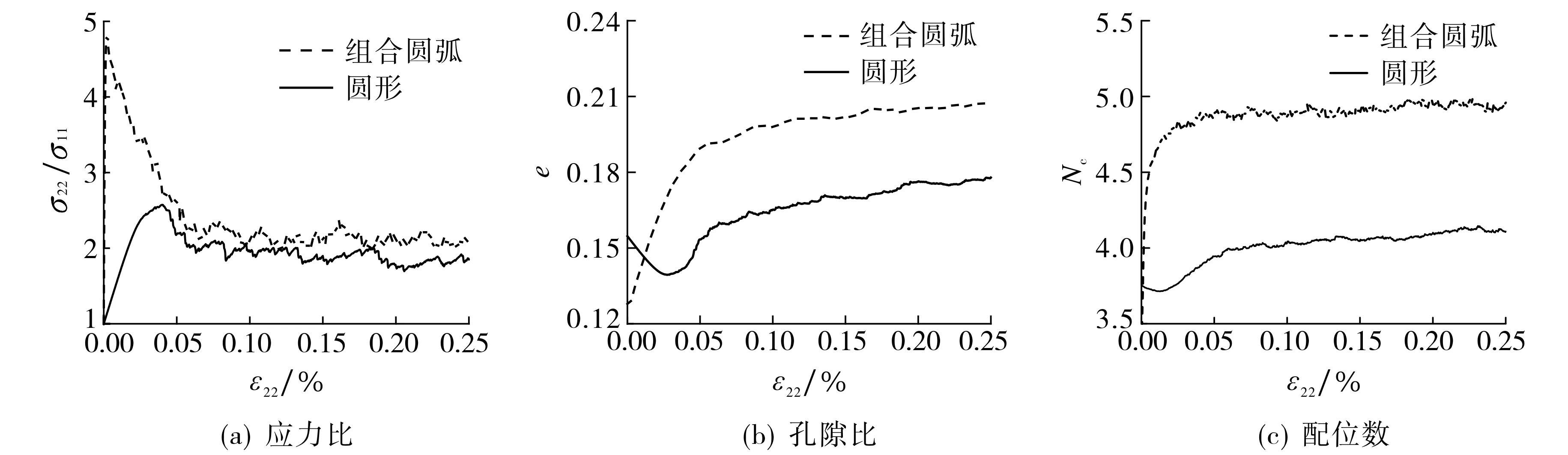
图8 不同形状二维颗粒体的应力、孔隙比、配位数与应变的关系曲线Fig.8 The stress, void ratio and coordination number versus strain under different 2D particle shapes

2.3 孔隙比

以两种孔隙比e=0.12(致密)和e=0.18(疏松)的干砂颗粒体为研究对象, 分析颗粒体初始孔隙比对颗粒体力学特性的影响．两种孔隙比的颗粒体均由1 000个随机排列的组合圆弧颗粒组成, 颗粒密度为2×103kg·m-3, 刚度比为0.25, 摩擦因数为0.5,围压为1.37 MPa．

图9为两种初始孔隙比下应力比和孔隙比与切向应变的关系曲线．由图9(a)可见,两种颗粒体区别明显,排列疏松的颗粒体经历硬化阶段后未出现软化现象,排列致密的颗粒体先经过硬化阶段,在切向应变变化的初始阶段达到峰值,随后发生软化,直至达到与颗粒排列疏松情况基本一致的稳定状态．表明砂土存在临界状态,此状态下不同初始孔隙比的颗粒体强度相同,即临界强度不受初始孔隙比的影响．由图9(b)可见,随加载的进行,初始孔隙比不同的两种颗粒体的孔隙比逐渐接近并趋于稳定．

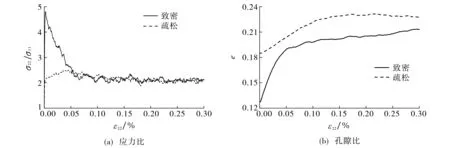
图9 不同孔隙比下应力比和孔隙比与应变的关系曲线(μ=0.5)Fig.9 The stress and void ratio versus strain under different void ratios (μ=0.5)

2.4 法向应力

法向应力是影响接触界面力学特性的重要因素,其限制颗粒运动, 影响颗粒体抗剪强度．选取1 002个颗粒组成的颗粒体为研究对象,初始孔隙比设为0.17,对不同法向应力条件下的接触界面进行数值模拟．图10给出了不同法向应力条件下应力-应变关系曲线．由图10可见,加载过程中参数不变,颗粒体首先经过硬化阶段,到达峰值后开始软化,最后达到临界状态;当法向应力较小时,应力-应变关系接近于理想弹塑性;随法向应力的增大,应变硬化特性增强,软化特性减弱,峰值剪应力和残余剪应力增大．

2.5 刚度比

图11给出了不同刚度比的应力比-应变关系曲线．由图11可见,随刚度比增大,峰值剪应力和残余剪应力变化不大,即刚度比对颗粒体峰值应力的影响较小．

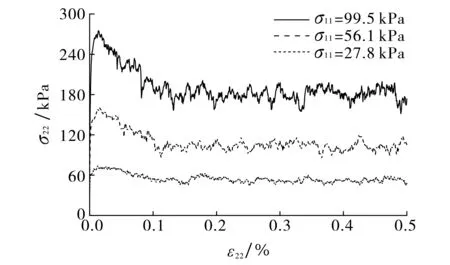
图10 不同法向应力条件下应力-应变曲线Fig.10 Stress versus strain with different normal stresses

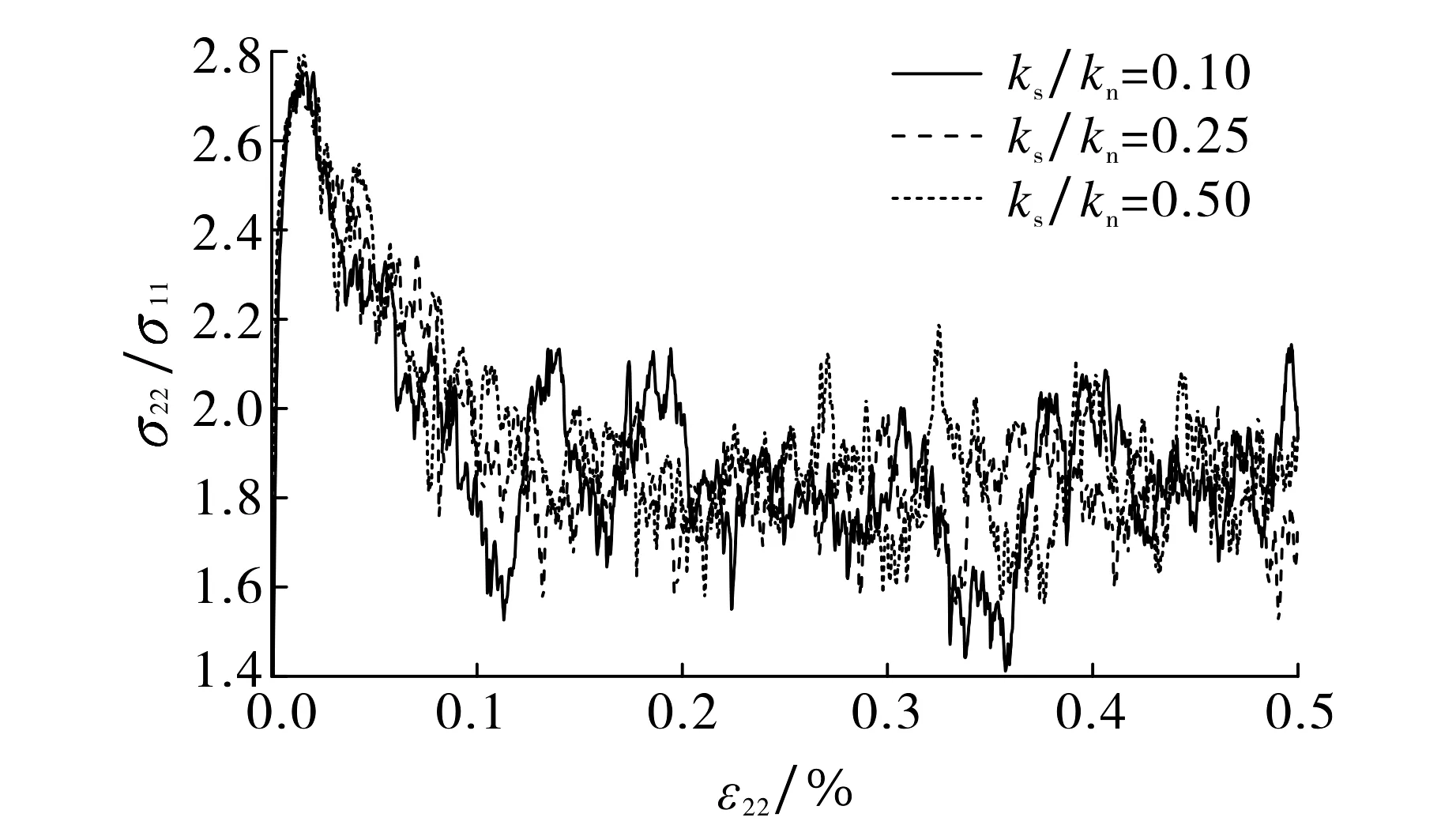
图11 不同刚度比的应力比-应变曲线Fig.11 Stress ratio-strain curves with different stiffness ratios

3 结论

1) 摩擦因数、颗粒形状、孔隙比和法向应力对接触界面的峰值强度影响较大,刚度比对接触界面的峰值强度影响较小; 摩擦因数、法向应力和刚度比对弹性模量影响较大,摩擦因数为0.1～0.3时影响最为显著．

2) 摩擦因数与内摩擦角近似成正比关系,颗粒间摩擦因数较大的土体,抗剪强度和剪胀性较大;组合圆弧颗粒更接近真实砂粒形状,咬合作用较强,受剪膨胀性高,推荐使用组合圆弧颗粒进行模拟;临界强度和临界孔隙比不受初始孔隙比的影响;法向应力越大,颗粒体抗剪强度越大．

3) 接触界面作为连接土与结构的介质,荷载作用下容易产生大变形, 造成结构失稳; 因此, 在确定接触界面材料时,可根据需要选择和调整材料的细观参数,以提高土-结构接触界面强度,增强结构整体的稳定性．