低矮房屋模型风压试验与数值仿真对比
杨 华, 杨俊伟, 朱卫军, 李迺璐, 冯科儒
(1. 扬州大学电气与能源动力工程学院, 江苏 扬州 225147; 2. 扬州大学广陵学院, 江苏 扬州225128)
龙卷风、台风等极端天气对建筑物造成极大的破坏,对低矮房屋而言,破坏主要是气流分离形成负压区,房屋承受的外压突变导致.对此,国内外研究人员围绕低矮房屋风荷载开展了大量数值仿真、现场实测及风洞试验研究.殷惠君等[1]利用多种湍流模型对德州理工大学(Taxas Tech university, TTU)实验屋标准模型的定常风场进行数值模拟; Huang等[2]对低矮建筑屋面坡度及长宽比例对风压的影响进行了研究;周晅毅等[3]采用精细划分网格的缩尺模型对建筑表面风压进行了大涡模拟和风洞试验; 王强等[4]针对日本建筑协会的建筑模型进行数值模拟计算,验证了不同湍流模型的精确性; Ricci[5]和Razavi[6]等对极端风况下低层建筑的风荷载进行了数值模拟分析.以上数值仿真研究可在低成本条件下对复杂建筑进行风环境评估和预测,但是低矮建筑物绕流是典型的钝体绕流,存在严重的脱流区域,准确预测低矮建筑物风压分布的难度较大.现场实测是在实际的低矮建筑周边布置测点,利用测风设备对实际风场进行现场测量,其中具有代表性的有TTU标准模型[7]、艾尔斯伯里实验房等,但由于试验地区的风场特性不同,现场实测成果也难以广泛应用到工程实际中.风洞试验是将分析模型按比例缩小放置在风洞中进行测压试验,利用风洞中模拟的流场进行试验获得风荷载数据[8-10],这是目前确定风荷载较为准确方法.Ozmen等[11]利用风洞试验对不同倾斜角的低矮平屋的风荷载进行了研究;黄汉杰等[12]利用风洞试验分析了大比例建筑模型表面的风压分布.
本文利用不同湍流模型对低矮建筑物TTU标准模型进行数值模拟.同时将TTU标准模型按比例为1∶15制作的缩小刚性模型放置在模拟B类风场中进行风洞试验,在TTU标准低矮建筑中轴线上布置多个测压孔,测量迎风前缘、屋顶、背风后缘附近处的风压值.将模拟结果与试验数据进行对比,分析低矮建筑物模型周围的流体运动规律,验证本文风洞试验数据的可靠性.
1 数值仿真
本文运用Fluent仿真软件对以TTU标准模型按缩小比例为1∶15制作的低矮建筑物模型进行三维定常数值模拟, 为保证数值模拟和风洞试验的环境具有一致性,整体计算区域按照如图1(a)所示的风洞尺寸建模,试验段长宽高分别为7, 3, 3 m, 模型所在截面阻塞比为2.7%.为满足不同风向角工况下标准模型的计算要求,在模型附近选用如图1(b)所示的圆柱体区域进行网格划分,圆柱体半径为1 m,高为3 m.采用结构化网格划分计算区域,共计189万个网格.并在靠近模型表面的区域进行局部网格加密,模型表面第一层网格高度为0.6 mm,伸展率为1.05.
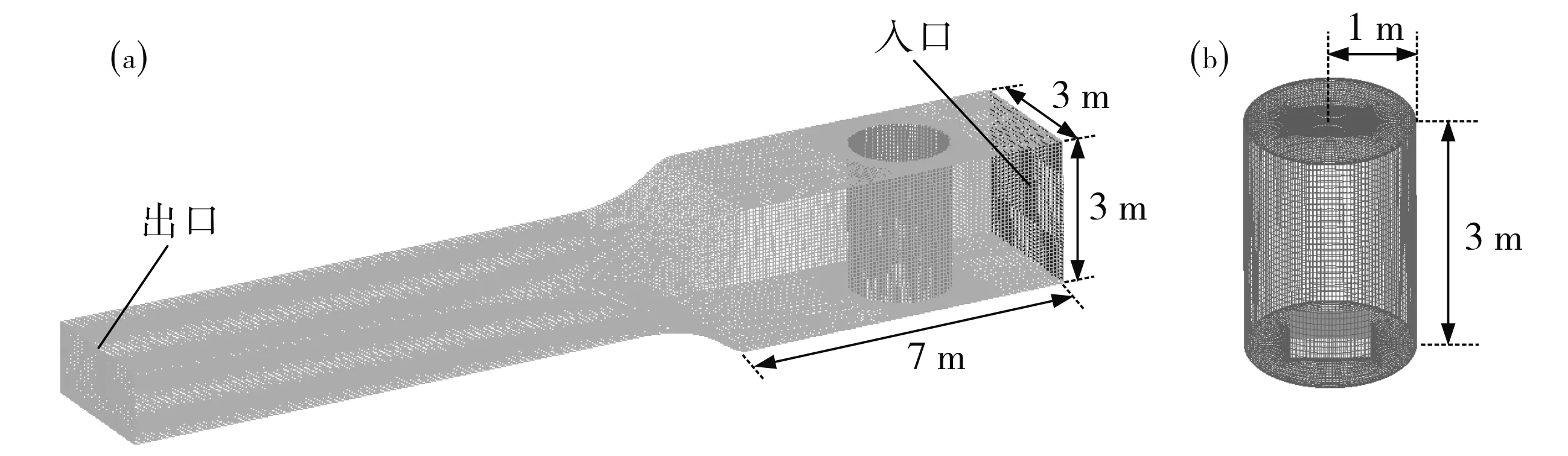
图1 数值计算区域(a)和TTU模型附近网格(b)Fig.1 Numerical calculation area (a) and grid near TTU model (b)
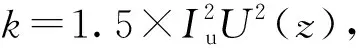
2 风洞试验

图2 风洞试验中B类风场布置及TTU标准模型Fig.2 Terrain B wind field and TTU standard model in wind tunnel test
利用扬州大学风洞的低速试验段进行风压测试,该试验段最大风速为25 m·s-1.图2为利用有机玻璃制作的刚性标准低矮建筑物模型和用尖劈和粗糙元模拟的B类地貌风场, 风洞中横向排列的三座尖劈高2 m, 底宽50 cm,距尖劈2 m的后方布置6排13列粗糙元, 粗糙元为边长6 cm的正方形木块, 粗糙元在风洞轴向上的间距为30 cm,横向间距50 cm.建筑物模型试验区位于粗糙元组正后方2 m处.
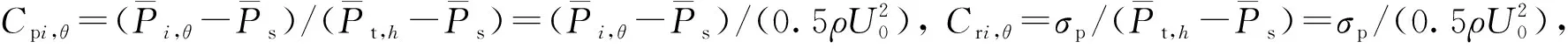
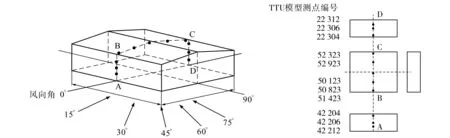
图3 标准低矮建筑风向角定义及测点示意Fig.3 Definition of wind angle and indication of measuring point for TTU
3 结果与讨论
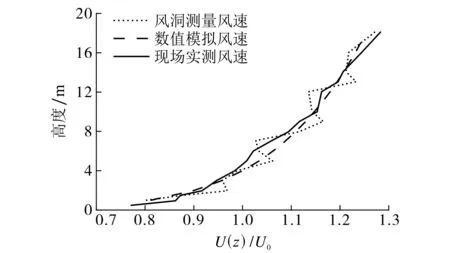
图4 试验区的风速剖面对比Fig.4 Comparison of wind velocity profile in the test area
图4为利用热线风速仪测量的模型试验区风速剖面.如图4所示,风速随高度的降低而减小,越接近地表位置,风速越小,这是地面黏性阻力作用所导致.此外,风洞实测风速剖面及数值模拟拟合风速与B类风场实测的风速分布一致,符合指数分布规律.
将TTU标准模型中的屋檐高度位置作为风速参考点,并将此处的风压作为无量纲参考风压.本文风洞试验(记为YZU-WT)采样6×104个数据, 将0°风向角下模型表面的平均风压、脉动风压分别与TTU-现场实测数据[7]、同济大学风洞(TJ-WT)实测数据[3]、Western University大学风洞(WUO-WT)实测数据[8], 以及采用Transitionk-kl-ω、标准k-ε湍流模型的计算数值进行对比, 结果如图5所示, 图5中横坐标表示以前缘B点为原点的模型中轴线相对壁面位置.由图5(a)可知,YZU-WT试验数据基本处于各类模型实测数据的包络线内,在迎风面区,YZU-WT风洞试验正压值大于其他现场实测数据.平均风压的计算值与试验数据较接近,但在迎风面和迎风的斜顶面,计算值与试验值略有偏差.由图5(b)可见,不同试验的脉动压力系数存在一定偏差,但其脉动趋势基本相同,均在迎风前缘点B处附近出现极大值,并随着相对壁面位置的增加,顺着来流风向脉动风压系数逐渐减小.
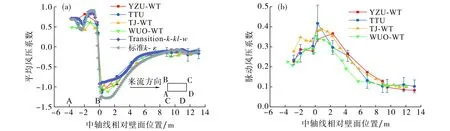
图5 平均风压系数(a)和脉动风压系数(b)的计算数据、试验数据对比Fig.5 Comparison of numerical calculation and measurements about average pressure coefficients (a) and pulse pressure coefficient (b)
图6为利用标准k-ε湍流模型计算得到的不同风向角工况下TTU标准模型的表面压力系数分布图.由图6可见, 迎风的垂直墙面风压均为正,顶面局部为负压.各风向角工况下的墙面受压情况不同,尤其在建筑物檐角附近的压力急剧变化.在斜风向工况下,建筑物会有两个迎风面受正压力,在迎风面中上部分的压力最大,并向两侧及底部减小,背风面及屋顶均受负压,且在迎风顶面的前檐处形成高负压区域,此区域内流体的惯性力要克服压强差和黏性力作用,导致靠近墙壁的流体质点停止向前移动或反向移动,而后再向下游泄出,形成涡流.这种情况对低层建筑物破坏性较大,须在实际工程中引起重视.
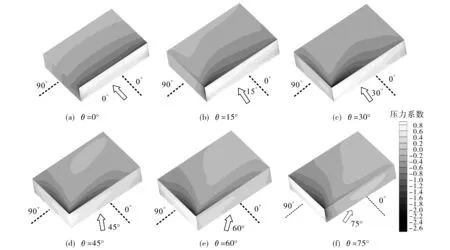
图6 不同风向角的TTU模型表面压力系数云图Fig.6 Cloud diagram of surface pressure coefficient of the TTU model at different income flow angle
图7给出了不同风向角下模型中轴线上各测点的风压系数模拟数据与风洞试验数据的对比结果.如图7所示, 各个风向角下的风洞试验结果与实测值均较接近, 风向角对中轴上的风压系数影响较大,迎风面的风压系数随风向角减小而减小.风向角倾斜时,建筑迎风面的风洞实测风压系数与计算结果略有偏差, 但建筑物顶部和背风面的风压系数吻合度较高.如图7(b)所示,风向角为30°时, YZU-WT实测风压系数与TTU实测数据的吻合度较高, 在迎风前缘处的YZU-WT实测数据值比TTU数值略大.比较2种计算模型的数据时发现,尽管Transitionk-kl-ω模型在数值计算中可得到与工程常用的SST低雷诺数模型相近的结果[13], 但处理钝体绕流问题时并未发现其优势, 图7(a)~(e)的结果显示标准k-ε模型计算结果与风洞实测数值更为接近, 2种模型计算结果的差别主要在负压区.这可能是因为Transitionk-kl-ω模型在模型近壁处所预测的湍流强度比k-ε模型大, 过大的湍流强度引起边界层内外的动能交换, 导致该模型的预测结果存在一定偏差.
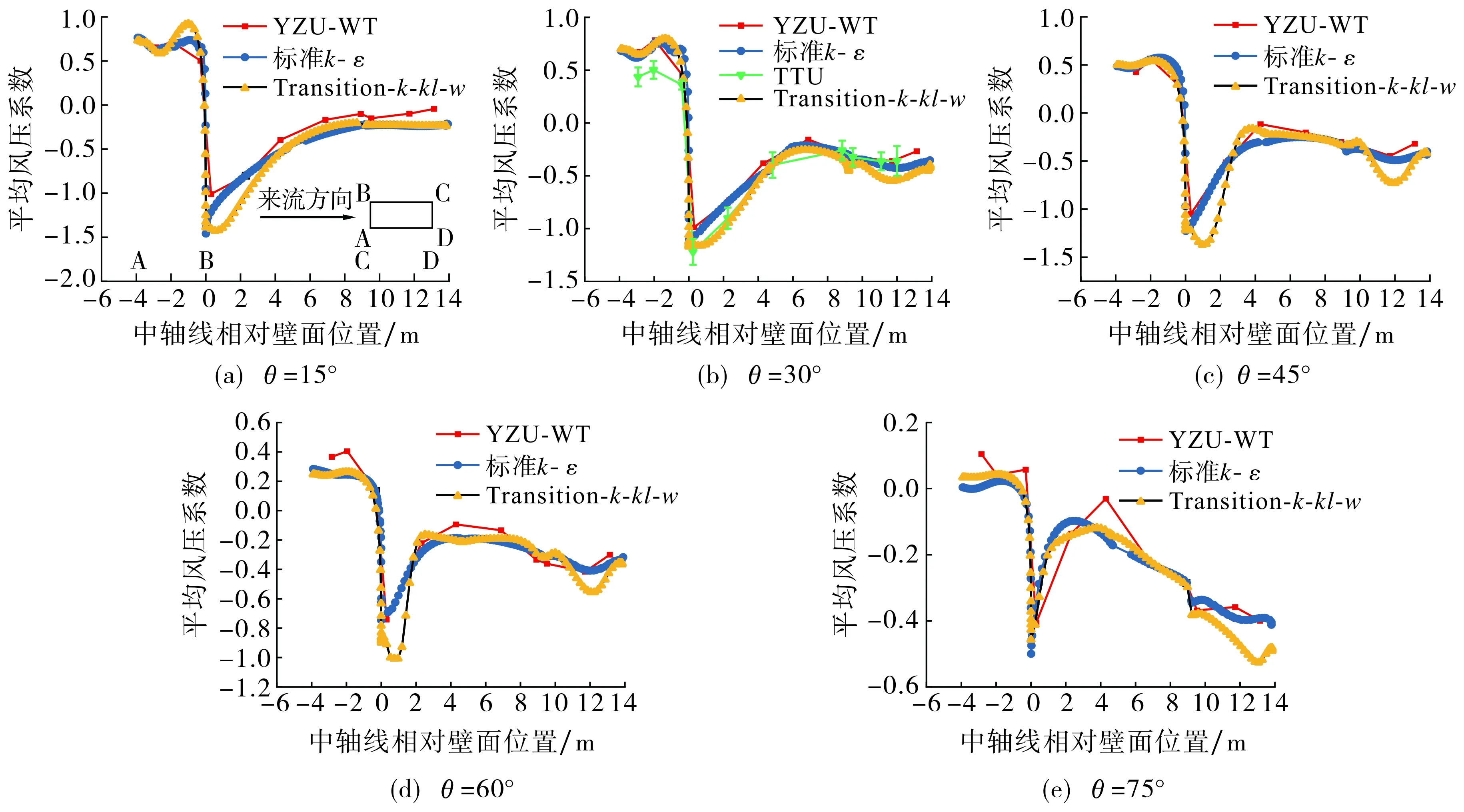
图7 不同风向角下TTU模型中轴线处风压系数数值计算与实测结果比较Fig.7 Numerical calculation and measurements on the central axis of TTU model at different income flow angle
4 结论
本文对TTU标准模型进行数值模拟,同时通过尖劈和粗糙元在扬州大学风洞中模拟B类风场,研究低矮建筑表面压力随风向角变化的一般规律,斜风工况下标准模型的表面压力系数云图表明,各风向角下的绕流情况不同, 靠近建筑物拐角处的涡流及压力变化明显.对于低矮建筑模型, 未见Transitionk-kl-ω模型处理钝体绕流问题的优势,而两方程标准k-ε湍流模型能较好模拟其在不同风向角下的流动特性和风压分布.实验表明本风洞试验对模拟低矮建筑风压分布具有较高的精度,可为工程设计提供可靠的风洞试验数据.

