基于模型平均的超高维数据特征筛选方法

高羽飞, 来 鹏, 何孟霜, 夏文俊

(南京信息工程大学数学与统计学院, 南京 210044)

为了对超高维数据进行分析, 众多学者展开了研究．Fan等[1]提出基于Pearson相关系数的SIS超高维特征筛选方法; Zhu等[2]提出可用于筛选非线性相关变量的SIRS特征筛选方法; Li等[3]在更一般的情况下,提出基于距离相关系数的DC方法, 实现了在无模型假设条件下对超高维数据进行变量筛选,并适用于对分组预测变量和多元响应变量的筛选; Wu等[4]提出基于条件分位数的自由模型特征筛选方法(conditional quantile screening, CQSIS), 该法可用于处理删失数据问题; 在此基础上, Liu等[5]提出适用于给定变量条件下的超高维分位数独立筛选方法; Cui等[6]依据超高维判别分析问题中响应变量是分类变量的特点,提出基于经验条件分布的边际特征筛选方法; Liu等[7]利用条件距离相关系数,构造出针对超高维数据的条件特征筛选过程．以上方法已经在很大程度上改进了传统方法对超高维数据分析的不足,但研究更稳健、有效的特征筛选方法仍然十分有意义．

近年来,模型平均思想在统计学上被广泛运用,它通过对不同的估计模型或者预测模型进行加权,综合考虑它们的性能,进而达到提高模型效率且降低模型误差的目的．Hansen等[8]提出在不确定异方差误差设置下,利用最小化交叉验证准则筛选权重对M个非嵌套近似模型加以组合来提高估计效果的JMA(jackknife model averaging)估计方法; Liang等[9]认为模型平均集成了模型选择过程中固有的不确定性, 通过对候选模型适当加权可以提高拟合模型的预测能力; Chen等[10]利用模型平均边际回归半参数惩罚方法对超高维动态时间序列数据进行了处理分析; Gao等[11]基于留一交叉验证, 提出可用于纵向数据以及包含异方差误差时间序列数据的模型平均方法．本文受模型平均思想的启发,拟将其与条件分位数筛选方法(CQSIS)相结合,给出基于模型平均的稳健超高维数据特征筛选方法．

1 基于模型平均的超高维数据特征筛选(MASIS)

1.1 筛选方法

1.2 理论性质

为了研究MASIS的理论性质,假设[4]:

(H1) 关于正的常数c和M以及α∈(0,1/4), 1≤s≤m, 有+∞>M≥maxk∈Aτs‖dk,τs‖≥mink∈Aτs‖dk,τs‖>2cn-α>0;

(H2) 在Qτ(Y)的领域内,F(y)是二阶可微的．Y的密度函数f(y)一致有界且不靠近0和无穷, 其导数f′(y)也是一致有界的．

定理1在条件(H1)和(H2)下, 对于正的常数c8,c9,c10和c11, 有

(1)

其中Sn,m=max{Sn,τs,s=1,…,m}．进而, 若mink∈Awk≥2cn-α,则

(2)

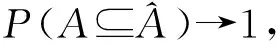
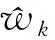
(3)

(4)

则

(5)

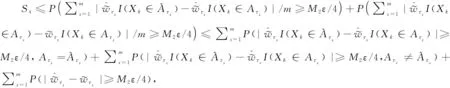
(6)

根据文献[4],得

(7)

(8)

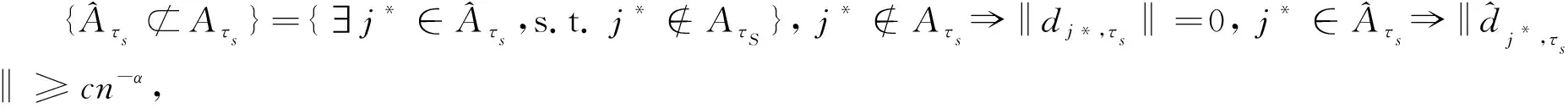
(9)

结合式(4)～(6), (9), 得

(10)

而

(11)

(12)

2 蒙特卡洛模拟

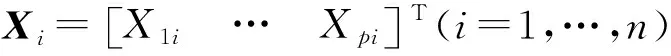
例1考虑线性回归模型Yi=X1i+3X2i+1.5X3i+2X4i+εi, 当ρ和残差εi满足: i)ρ=0.5,εi服从t(1)分布; ii)ρ=0.8,εi服从标准柯西分布时, 模拟结果见表1和表2．从表1和表2中的结果不难看出, MASIS、SIRS以及DC筛选出所有真实重要变量需要的模型规模相似且都较小, 与真实模型非常接近; 而SIS筛选时, 虽然4个真实的重要变量也能筛选出来, 但稳定性不高．比较Pa值, MASIS和SIRS方法均以趋于1的概率在200次试验中将真实重要变量筛选出来, 而DC方法稍差, SIS方法表现最差．

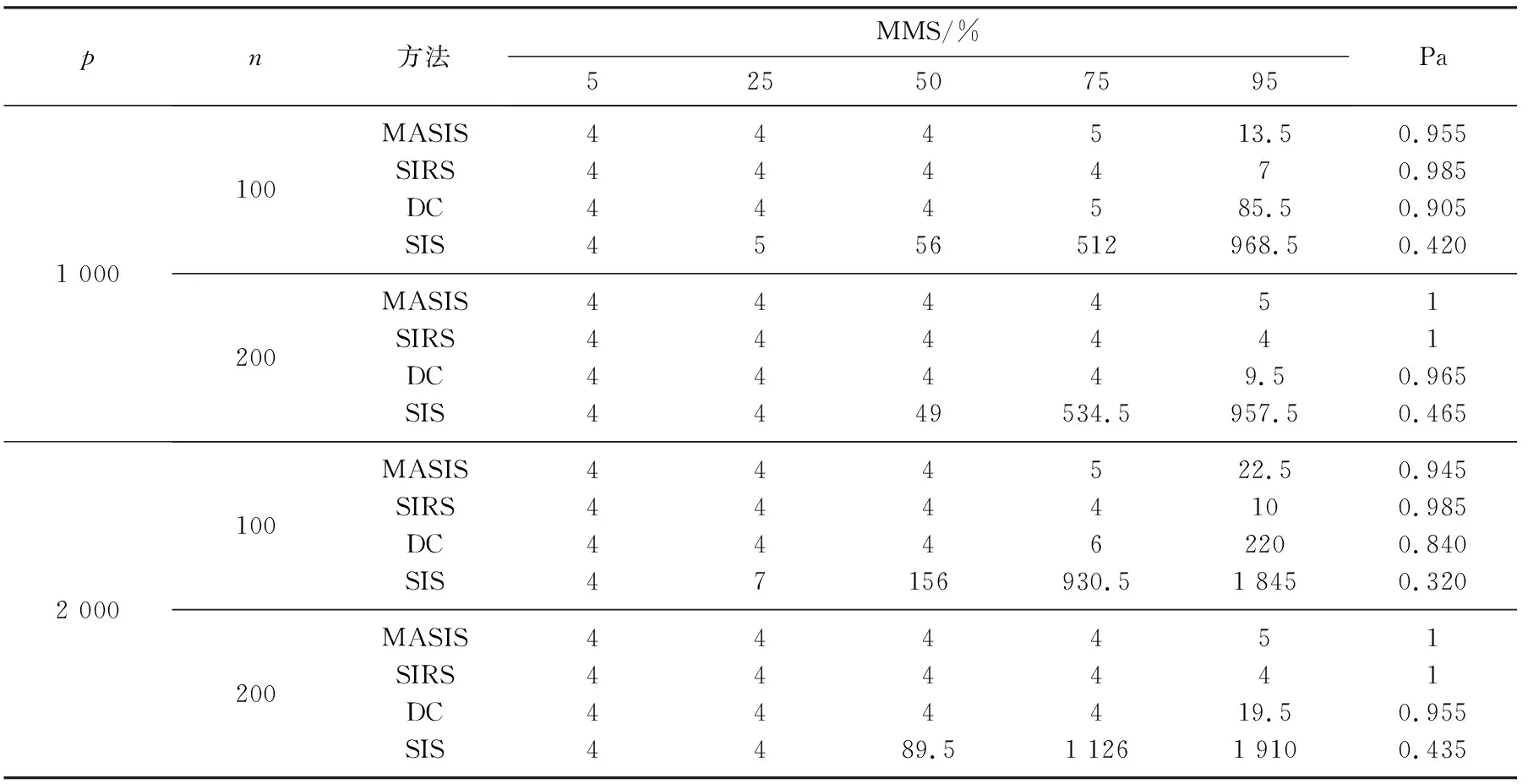
表1 ρ=0.5时残差εi服从t(1)分布的筛选模拟结果

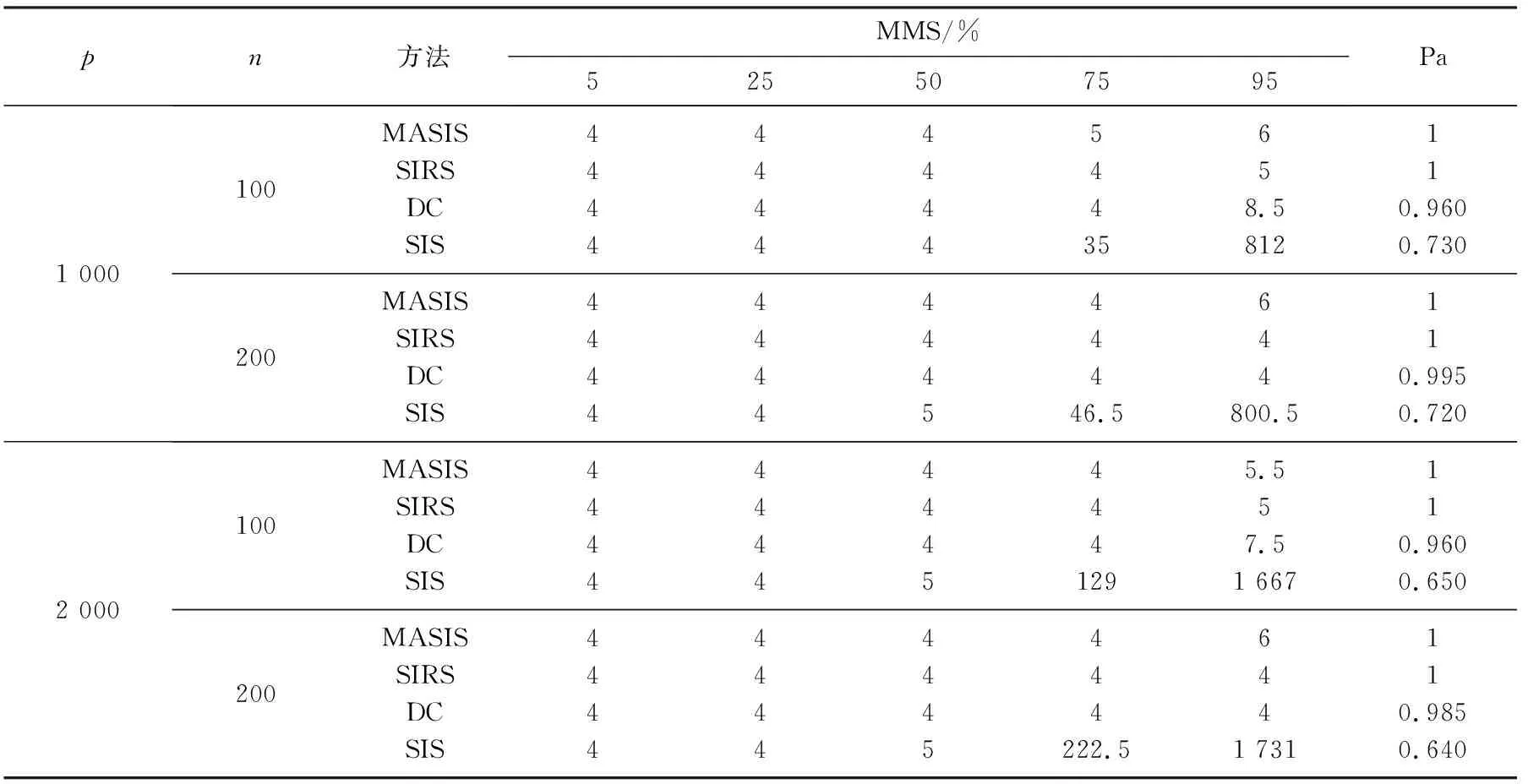
表2 ρ=0.8时残差εi服从标准柯西分布的筛选模拟结果

例2考虑带有交互项的可加模型Yi=3sinX1i+4cos2X2i+2exp(X3iX4i)+εi, 当ρ和残差εi满足: i)ρ=0.8,εi服从标准正态分布; ii)ρ=0.9,εi服从标准柯西分布时, 模拟结果见表3和表4．从模拟结果可以看出, MASIS方法筛选出所有真实重要变量需要的模型规模相似且均较小, 与真实模型非常接近; DC方法的总体筛选效果一般, 且稳定性较差, 而SIS和SIRS方法虽然也可以筛选出4个真实的重要变量,但稳定性都很低．比较Pa值,很明显MASIS方法几乎以趋于1的概率在200次试验中能将真实重要变量全部筛选出, 而DC方法稍差, SIS和SIRS方法表现很差．

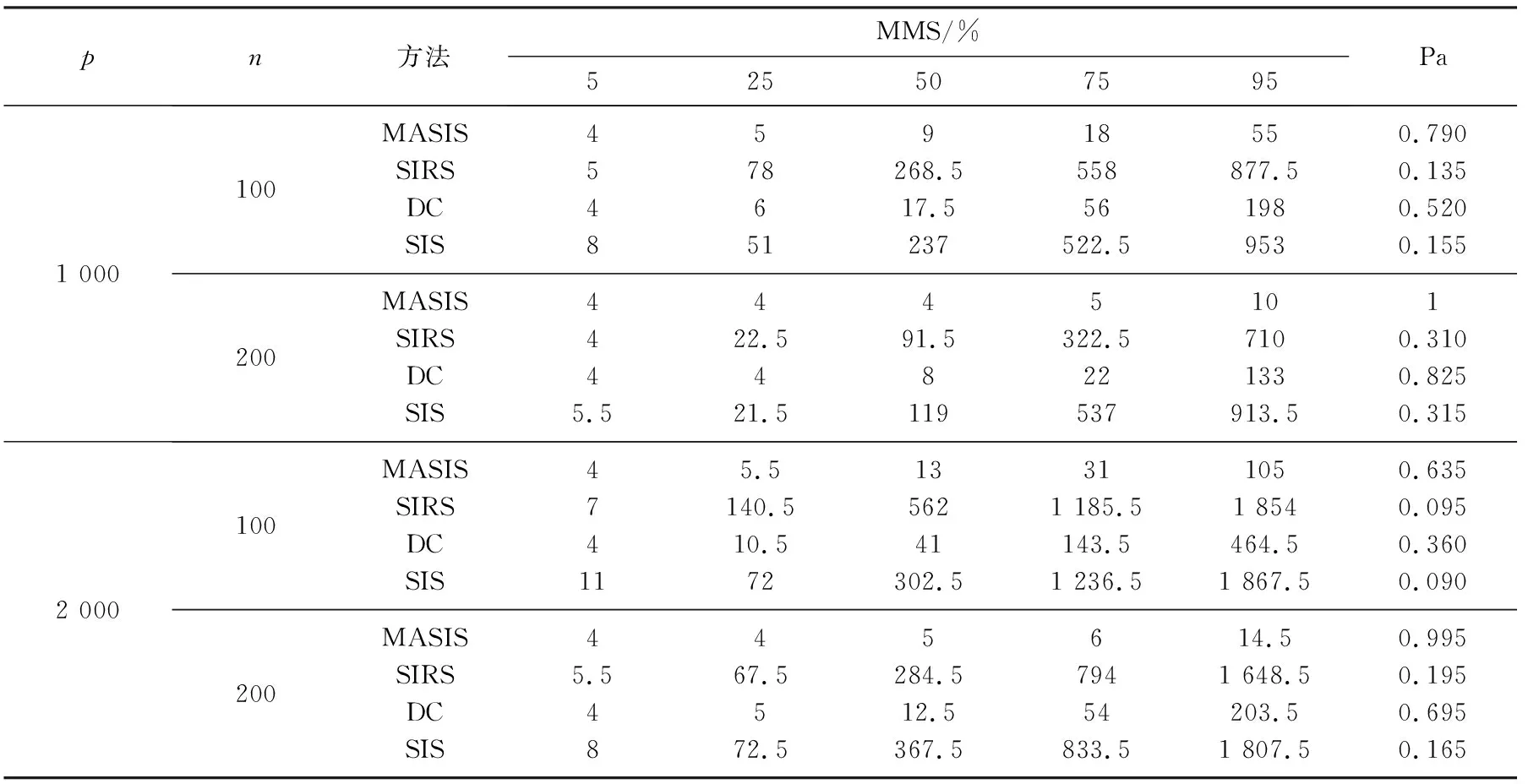
表3 ρ=0.8时残差εi服从标准正态分布的筛选模拟结果

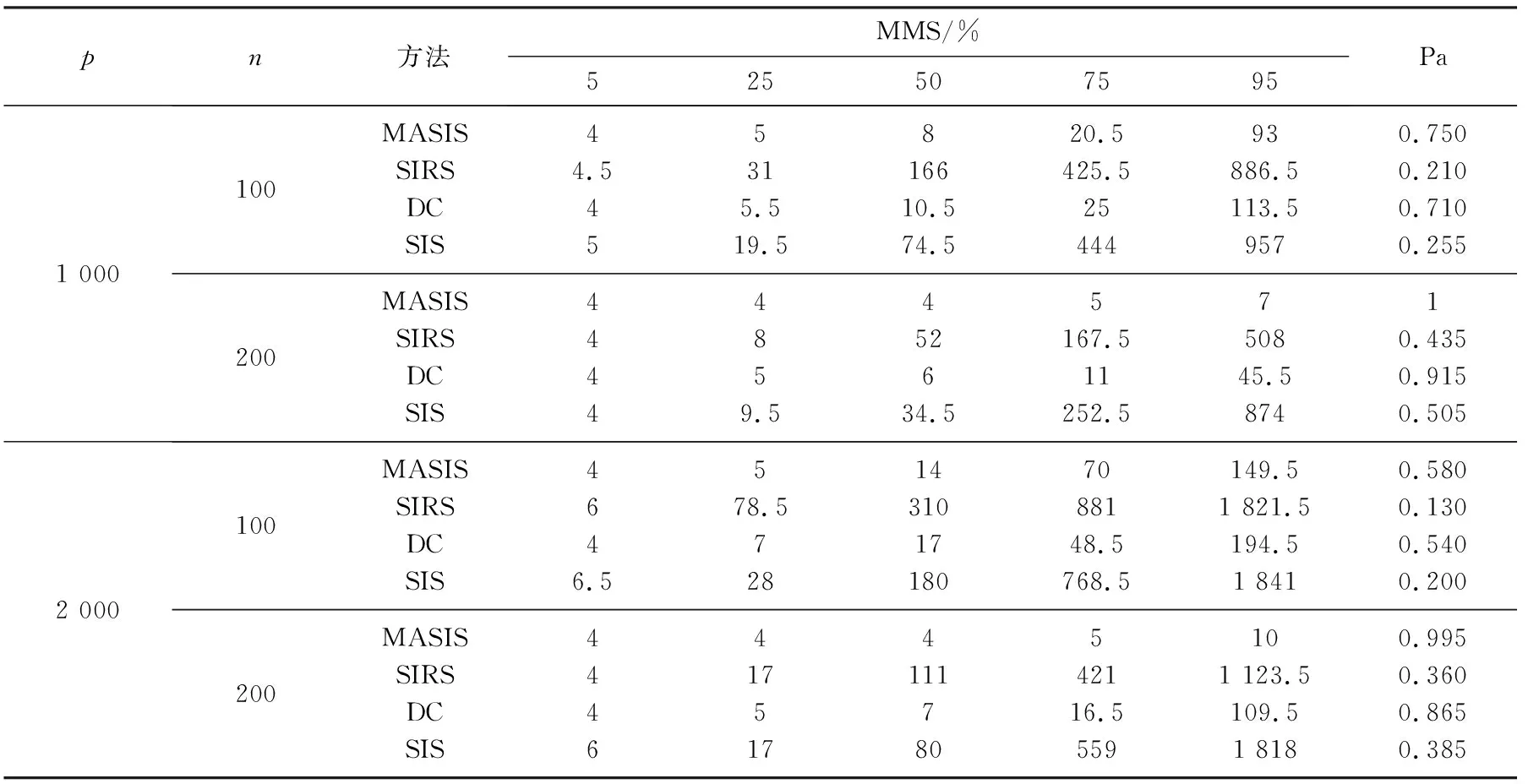
表4 ρ=0.9残差εi服从标准柯西分布的筛选模拟结果

3 实例分析

将MASIS特征筛选方法用于对转基因小鼠心肌病数据的分析中, 筛选出小鼠体内与Ro1相关的基因．转基因小鼠心肌病数据中共有30个小鼠样本,对应的基因数有6 319个, 从实例分析的结果可知[4], 与Ro1相关的基因为Msa.2134.0, Msa.2877.0, Msa.26025.0, Msa.15442.0和Msa.10108.0．

考虑MASIS方法包括第一步的局部筛选以及第二步的加权后筛选, 为了避免遗漏可能的重要变量, 采用2个不同排序筛选变量数d．第一步选择较大的d=100, 第二步选择较小的d值来确定筛选模型的规模, 筛选结果如表5所示．结果表明,当筛选模型的规模达到15时,5个相关基因全被筛选出,而文献[7]利用条件分位数筛选方法(CQSIS)完全筛选出所需模型的最小规模为29．本文方法缩小了筛选模型的规模, 说明MASIS筛选方法在一定程度上改进了条件分位数筛选方法(CQSIS)．

表5 MASIS方法对转基因小鼠心肌病数据的筛选结果

为了进一步研究这15个基因与Ro1之间的关系, 分别建立LASSO、神经网络和分类回归树模型．建模预测结果如图1所示．模拟结果证实, 分类回归树模型的预测情况最好．

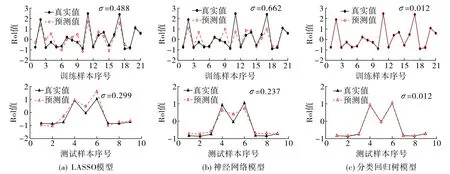
图1 回归预测图及标准差σ(上图为训练集，下图为测试集)Fig.1 Regression forecasting and standard deviation (the training set is shown in the figure above, and the test set is shown in the figure below)

4 结论

本文提出基于模型平均思想的稳健超高维特征筛选方法(MASIS), 分析其确定性筛选性质,并给出了MASIS方法理论性质的证明．通过蒙特卡洛模拟,验证了MASIS方法在处理线性问题和非线性问题时具有很好的稳健性,同时该方法相比较于其他方法,能更好地处理超高维数据中经常出现的异构性和交互作用等问题．自由模型假设的条件,使得该方法具有更广泛的使用范围．数值模拟和实例分析的特征筛选结果显示,MASIS方法比之前的筛选方法能更有效、更稳健地筛选出理想的特征变量,对现有方法进行了恰当地改进．