等价关系C*代数上的*同态
2020-09-08 02:29:50侯成军
扬州大学学报(自然科学版) 2020年3期
韩 笑, 侯成军
(扬州大学数学科学学院, 江苏 扬州 225002)
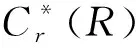

1 基本概念
本文涉及的等价关系C*-代数理论中的概念及术语可参见文献[1,6,10].设X是一个第二可数的局部紧的豪斯道夫空间, 令R⊆X×X表示X上的一个等价关系,R2={(x,y),(y,z)|(x,y),(y,z)∈R}⊆R×R,R0={(x,x)|x∈X}为R的单位空间.若将x与(x,x)等同起来, 则X≡R0可以看作是R中的子集.令r和s分别表示上R的range映射和source映射:r(x,y)=(x,x),s(x,y)=(y,y), 其中(x,y)∈R.称上R的映射(x,y)→(y,x)为逆映射,R2到R上的映射((x,y),(y,z))→(x,z)为R上的乘法映射.
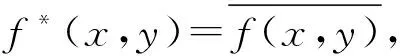

2 主要结果及证明
设X和Y是局部紧的豪斯道夫空间,π是X到Y上的连续映射, 称π是proper映射.若K⊆Y是紧的, 则π-1(K)⊆X也是紧的. 对于x∈X, 有mπ(x)=#{y∈X|(x,y)∈R,π(x)=π(y)}, 其中#S表示集合S的基数.
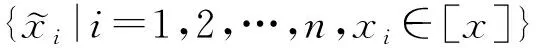


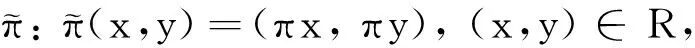

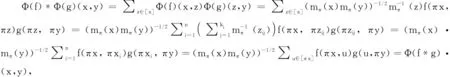

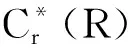
由定理2, 可得如下推论.
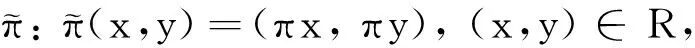

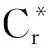
猜你喜欢
语数外学习·高中版下旬(2023年7期)2023-09-25 00:45:13
安庆师范大学学报(自然科学版)(2021年1期)2021-11-28 11:06:20
吉首大学学报(自然科学版)(2020年2期)2020-09-14 08:15:02
五邑大学学报(自然科学版)(2020年1期)2020-06-17 04:13:04
南京大学学报(数学半年刊)(2020年1期)2020-03-19 02:24:44
四川师范大学学报(自然科学版)(2019年1期)2019-02-22 00:33:09
汉字汉语研究(2018年1期)2018-05-26 08:50:07
数学物理学报(2018年2期)2018-05-14 07:32:07
信息安全研究(2016年3期)2016-12-01 06:06:28
衡阳师范学院学报(2016年3期)2016-07-10 07:16:27

