偏心受压桁架式钢骨混凝土柱正截面受力性能分析

曹思琦, 曹大富, 王 琨, 孟睿智, 鲁 琼

(扬州大学建筑科学与工程学院, 江苏 扬州 225127)

近年来, 拼装结构体系是建筑业的研究热点,分为混凝土结构拼装和钢结构拼装．其中混凝土结构拼装需要大量湿作业施工,无法体现拼装体系的优点;钢结构适宜于工业化拼装,但其防腐、防火性能较差[1-3]．桁架式钢骨混凝土构件是空腹式钢骨混凝土的一种,与普通钢筋混凝土结构相比,空腹式钢骨结构中配置的钢骨可显著提高构件的承载力,同时也有效解决了实腹式钢骨混凝土梁柱节点交叉穿筋的问题[4-5]．国内外大量试验研究表明, 钢骨混凝土柱、钢管混凝土柱与钢筋混凝土柱相比具有良好的受力性能和承载能力,但针对空腹式钢骨混凝土柱的研究较少．Campione[6]和戴彬[7]等提出多种空间钢构架混凝土柱的设计形式, 通过试验发现角钢和缀条的参数对混凝土柱承载力具有重要影响．现有桁架式混凝土柱结构的研究主要集中于梁柱节点的力学机理[8],忽视了柱在结构中力学传递的重要性．目前,实腹式钢骨混凝土柱结构被广泛应用于桥梁和房屋结构中[9-10],但空腹式钢骨混凝土柱结构的研究和应用并不多见,尤其是桁架式钢骨混凝土长柱,其研究具有一定的局限性．本文拟通过试验与数值模拟相结合的方法,研究桁架式钢骨混凝土长柱在偏心荷载下的力学性能,分析试件的破坏过程、形态以及重要部位的应力应变数据,研究试件的强度和刚度等性能,推导试件柱受压承载力公式,并通过试验验证数值模拟方法的适用性和可靠性．

1 试验概况

1.1 试件设计与制作

试验共设计制作4根大偏心受压桁架式钢骨混凝土柱, 编号分别为SRCC1～SRCC4．4根柱均设有增大柱头, 柱的截面尺寸均为300 mm×300 mm, 柱高1 700 mm,腹杆选用L30×3的角钢,间距为400 mm, 纵向角钢为L40×4,构件SRCC1～SRCC4的偏心距分别为100, 130, 165, 200 mm．偏压柱的结构见图1．采用C35混凝土,与构件同条件下养护一组(3个)混凝土立方体试块, 进行抗压试验,标准抗压强度实测值分别为44.2, 39.9, 37.5 MPa,抗压强度平均值为40.5 MPa, 轴心抗压强度为30.78 MPa．角钢及钢板采用Q235钢材, 实测材料性能指标见表1．

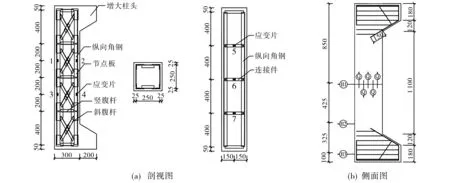
图1 桁架式钢骨混凝土偏压柱结构及测点布置(单位: mm)Fig.1 Structure and measuring point arrangement of truss steel reinforced concrete eccentric compression column

表1 钢材力学性能

1.2 测点位置

钢桁架应变测点位置如图1(a)所示．试件柱的两根纵向角钢的标定形心位置1～4处分别粘贴应变片,用于研究角钢应变; 钢桁架侧面连接件的形心位置5～7处分别粘贴应变片,用于分析连接件约束混凝土作用的变化规律．混凝土表面百分表和千分表的测点位置如图1(b)所示．构件柱的跨中、柱身四分点位置及侧面距柱底100 mm处各布置1个百分表(用B表示), 用于测量每级荷载作用下对应测点的侧向位移; 柱侧面中部从左至右布置5个千分表(用Q表示),用于测量混凝土表面的应变．

1.3 试验加载

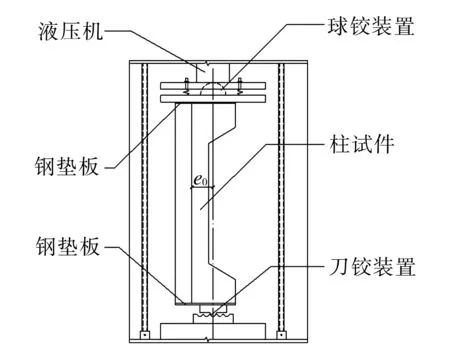
图2 试验加载装置Fig.2 Test setup

图2为试验加载装置示意图, 其中e0为轴向力对截面重心的偏心距．构件柱均为上下铰接, 上端是液压机自带球铰装置,下方为定制刀铰装置; 支座与试件混凝土之间垫设钢板,避免局部受压破坏; 试件柱两端粘贴钢板,加载时钢板对准仪器设定位置,使其受到对称的同轴力作用,以确保加载的精准性及锚固的合理性．静载试验直接由液压机完成,通过调节钢板及试件柱的位置以满足不同偏心率的要求．首先,对桁架式钢骨混凝土试件柱进行预加载,预载值不超过开裂荷载的70%,检验试件柱内部结构是否接触良好、仪器能否正常工作并获得准确的数据; 其次, 进入正式加载阶段,根据开裂荷载、标准荷载和极限荷载进行分级,其中标准荷载取预估极限荷载的70%,加载时竖向荷载从0开始,逐级增加,直到破坏为止．试件未开裂前,分为3级加载,达到开裂荷载计算值的90%后,每级荷载取标准荷载的5%,直至试件出现第1条裂缝;试件出现裂缝后,取标准荷载的20%进行加载,达到标准荷载后每级荷载取标准荷载的10%,达到极限荷载的90%后,每级荷载取标准荷载的5%,直至构件破坏．为了使试件变形能够充分发挥并趋于稳定,试件开裂前每级加载持荷时间不少于30 min, 开裂后每级加载持荷时间不少于10 min．其中构件SRCC1加载耗时270 min, SRCC2加载耗时230 min, SRCC3加载耗时220 min, SRCC4加载耗时200 min, 平均耗时230 min．

2 试验结果与分析

2.1 裂缝分布和破坏形态

图3为试件的主要破坏形态．加载初期构件处于弹性状态;荷载增大到极限承载力Nu的30%时, 构件受拉区出现裂缝,后期逐渐发展为主要裂缝, 其中试件SRCC3从柱侧身延伸至柱表面共出现5条裂缝, 最大裂缝长度达到7 cm; 当荷载达到Nu的50%时, 原有裂缝继续开展,不同偏心率的最大裂缝不等; 加载至Nu的70%时, 横向裂缝延伸缓慢, 中和轴迅速移动,受压区高度明显减小,此时受拉区角钢开始屈服, 最大裂缝宽度达到0.25 mm; 继续增荷, 受压区出现竖向裂缝, 直到受压区混凝土被压溃, 此时达到构件的Nu．试件屈服前, 偏心率越大, 裂缝宽度越大,最大裂缝宽度为0.26 mm; 试件屈服后,裂缝宽度也随偏心率增大而增大,但最大宽度不超过0.3 mm, 说明桁架式钢骨混凝土偏压柱具有良好的抗裂性能．由此可见, 核心混凝土柱三向受力作用的大小影响屈服后构件的抗裂性能, 受压作用越大,混凝土柱屈服后最大裂缝宽度越小,试件受弯性能越好．

图3 试件的主要破坏形态Fig.3 Main failure modes of specimens

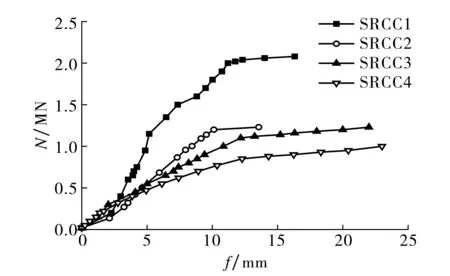
图4 偏压柱荷载-侧向位移曲线Fig.4 Load-lateral displacement curve of eccentric compression column

2.2 荷载-位移曲线

图4为偏压柱荷载N与侧向位移f的关系曲线．柱端竖向荷载由液压机测得, 侧向位移值由百分表B1测得．从图4可以看出, 偏压构件开裂前, 其侧向挠度近似呈直线增长,试验柱处于弹性工作阶段;继续增荷,受拉区混凝土开裂,受拉区角钢开始发挥作用, 荷载-侧向位移曲线出现第1个拐点, 与之对应的荷载为开裂荷载; 第1个拐点出现后偏压柱的刚度有所降低,但侧向挠度依旧随荷载的增大近似呈直线增长,偏压柱具有一定的塑性特征;随着竖向荷载的增大,受拉区纵向角钢达到屈服,内力臂增加,中和轴缓慢向试件受压区移动,受压区角钢也开始慢慢屈服,侧向挠度进一步加大;当受压区混凝土达到抗压极限值时,混凝土被压溃．由此得出,同等竖向荷载作用下,偏心距越大,其侧向位移越大．

2.3 混凝土应变曲线

图5为偏压柱截面高度h与混凝土应变ε的关系曲线．混凝土表面应变情况由图1(b)试件跨中混凝土表面粘贴的5个千分表测得,其中混凝土应变受拉力时为正,受压力时为负．从图5可以看出, 偏压柱的截面高度-混凝土应变随荷载增加而增大, 受压区高度随偏心率的增大而减小．分析试件破坏过程,得出偏压柱中部截面的平均应变基本符合平截面假设．

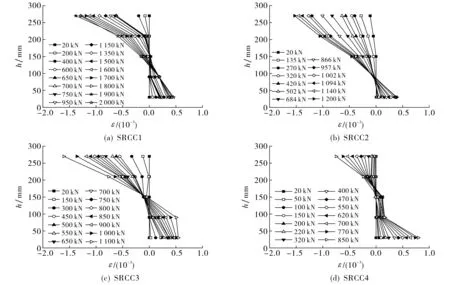
图5 偏压柱截面高度-混凝土应变曲线Fig.5 Section height-concrete strain curve of eccentric compression column

2.4 荷载-应变曲线

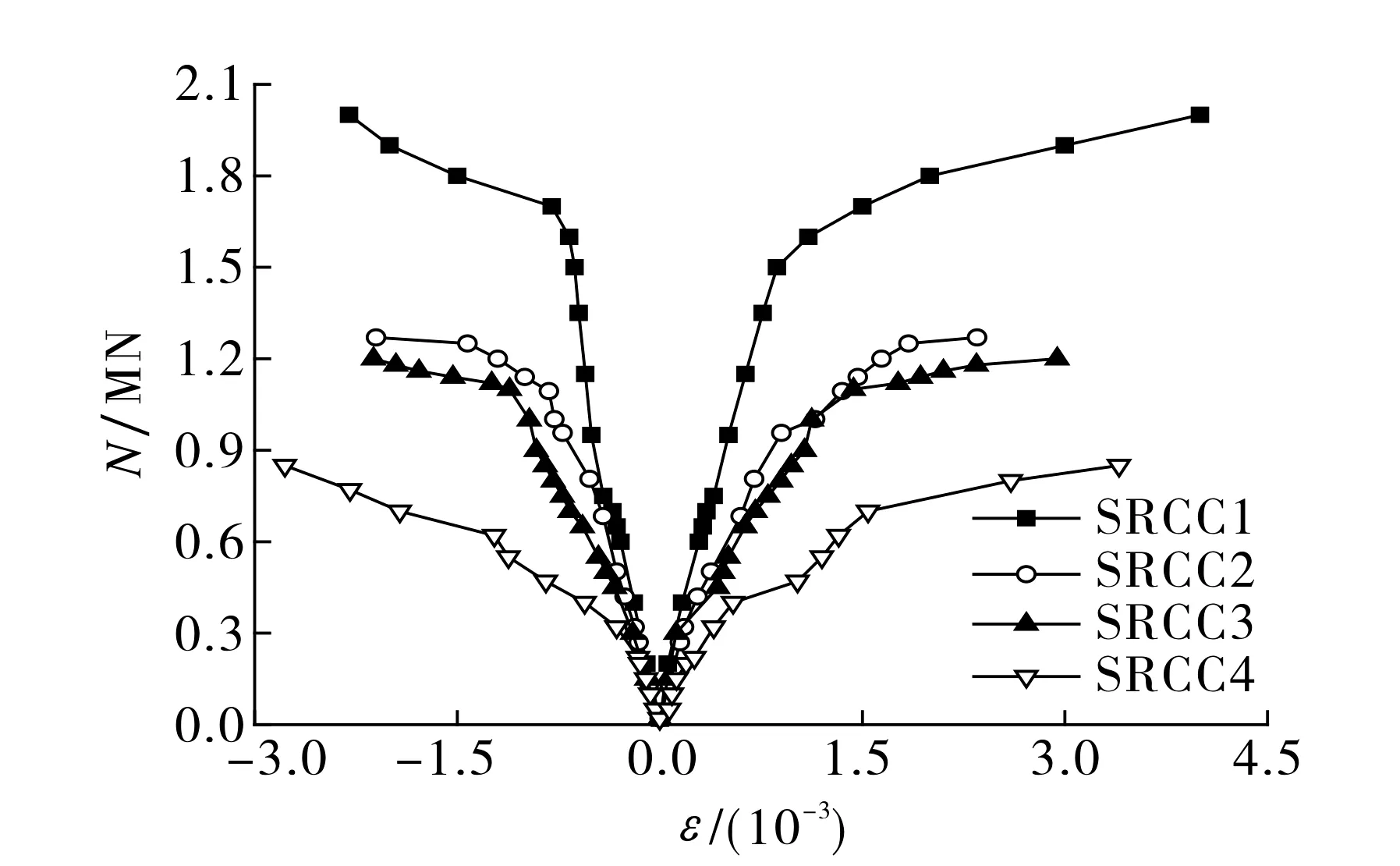
图6 偏压柱角钢荷载-应变曲线Fig.6 Load-strain curve of angle steel for eccentric compression column

图6为偏压柱角钢荷载与应变的关系曲线, 桁架式钢骨混凝土柱和荷载具有对称性,对称的拉应变或压应变取平均值．从图6可以看出, 偏压柱开裂前, 各角钢应变测点随荷载增大近似呈直线增长, 偏压柱处于弹性阶段; 当荷载达到Nu的70%时, 受拉区纵向角钢屈服; 当荷载达到Nu的85%时, 受压区纵向角钢屈服,偏压柱刚度逐渐降低,拉应变呈非线性增长;随着荷载继续增大,角钢进入强化阶段, 拉应变也随荷载的增大而增大, 荷载达到Nu时受压区混凝土压坏, 试件破坏．4根偏压柱表现出相似的受力趋势,角钢的最大应变为2.5×10-3～4.0×10-3, 但各构件的Nu存在明显差异,Nu随偏心距的增大而减小,符合试验设计阶段的推测．

2.5 开裂荷载、屈服荷载和极限荷载

表2为各试验柱的开裂荷载Ncr,e、屈服荷载Ny,e和极限荷载Nu,e的实测值．从表2可以看出, 构件的开裂荷载、屈服荷载和极限荷载随偏心距的增大而减小, 开裂荷载与极限荷载的比值约为0.3, 屈服荷载与极限荷载的比值约为0.7, 该数值与普通钢筋混凝土受弯构件的荷载比值相近, 验证了桁架式钢骨混凝土偏压柱结构的荷载可靠性．

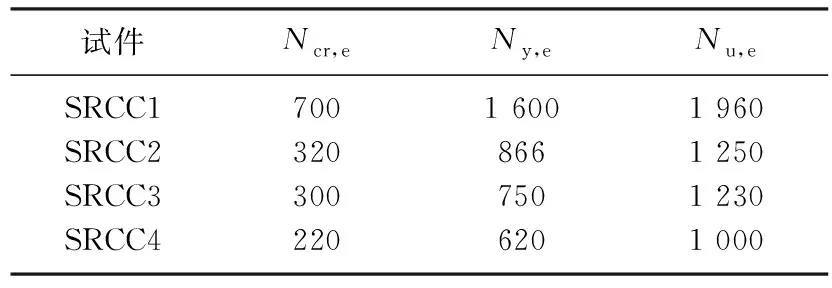
表2 各试件开裂、屈服和极限荷载

3 有限元分析

3.1 模型建立

混凝土本构采用混凝土损伤塑性模型,箍筋外保护层无约束混凝土区和箍筋约束混凝土区的混凝土采用Mander模型, 混凝土受拉应力-应变关系依据《混凝土结构设计规范》(GB50010—2010)．混凝土的膨胀角φ取36°, 流动势偏量值ζ取0.1,初始的双轴抗压屈服强度与单轴抗压屈服强度之比σb0/σc0取1.16, 拉伸子午面上和压缩子午面上的第二应力不变量之比Kc取0.666 7, 黏性因数μ取0.001．试验构件的钢骨架中的竖腹杆、斜腹杆、连接件等在钢骨混凝土中起箍筋作用,在满足精度要求的前提下, 为了便于计算, 钢骨采用理想弹塑性模型．

将角钢、节点板和连接件组合成钢骨作为嵌入单元,采用嵌入区域约束(embedded region)来模拟钢骨与混凝土之间的相互关系,解决钢骨与混凝土的粘结问题．建模过程中,为避免支座处及加载点应力集中,在柱上下端设置刚度较大的刚性垫块．假定支座上方和加载点下钢块与混凝土在接触面上点的平动自由度相同,采用绑定(tie)约束进行模拟,简化模型,便于计算．

3.2 计算结果

3.2.1 破坏形态

图7为偏压柱混凝土等效塑性应变图．从图7可以看出, 荷载作用下构件柱出现受拉区和受压区, 混凝土表面中部一侧受压, 混凝土在受压区应力最大,发生破坏,破坏情况与试验破坏形态较为一致．图8为偏压柱混凝土钢骨应力云图．从图8可以看出, 偏压柱的受拉区与受压区差别明显,整个模型的计算过程是从受拉角钢屈服,到受压角钢屈服,最后到受压区混凝土被压碎,模拟结果与试验情况基本吻合．

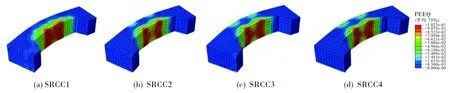
图7 偏压柱混凝土等效塑性应变图Fig.7 Concrete equivalent plastic strain diagram of eccentric compression columns

图8 偏压柱混凝土钢骨应力云图Fig.8 Steel bone stress cloud diagram of eccentric compression columns

3.2.2 极限荷载

表3 柱极限荷载实测值与分析值对比

3.2.3 荷载-位移曲线

图9为有限元模拟结果与试验结果的偏压柱荷载-位移曲线．从图9可以看出,试验结果与模拟分析结果基本吻合．偏心率越大,极限承载力越小; 相同荷载条件下偏心率越大,变形越大．

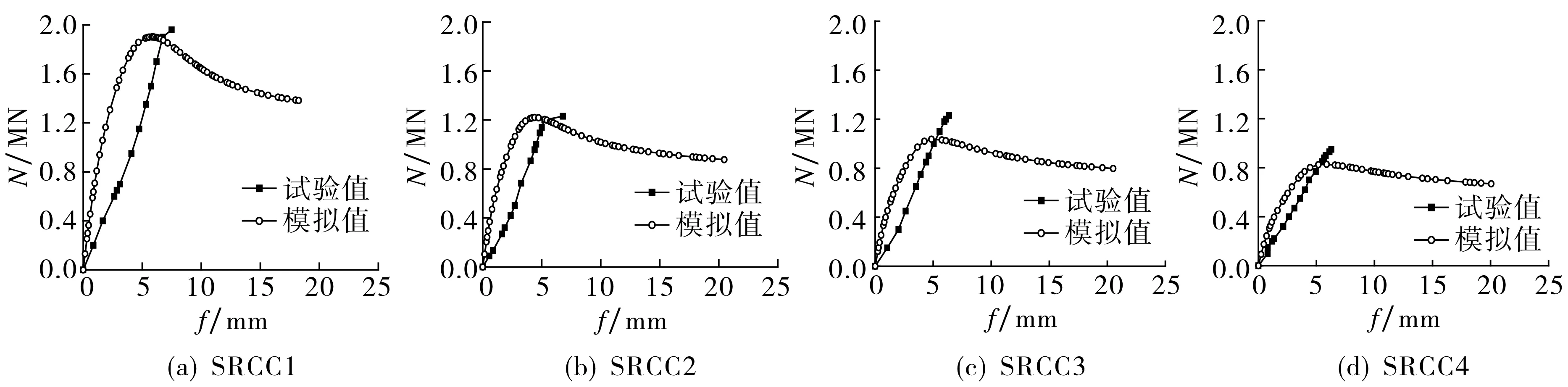
图9 偏压柱荷载-位移曲线对比图Fig.9 Steel bone stress cloud diagram of eccentric compression columns

4 混凝土长柱偏压承载力计算

计算桁架式钢骨混凝土柱受弯承载力采用的基本假设为: 1) 截面保持平面; 2) 不考虑混凝土的抗拉强度; 3) 混凝土受压应力-应变关系与《混凝土结构设计规范》(GB50010—2010)中正截面受弯承载力计算中的本构关系相同; 4) 纵向角钢的平均应力取角钢平均应变与其弹性模量的乘积, 且不超过其屈服强度; 5) 角钢拉应力达到其抗拉强度设计值fy．

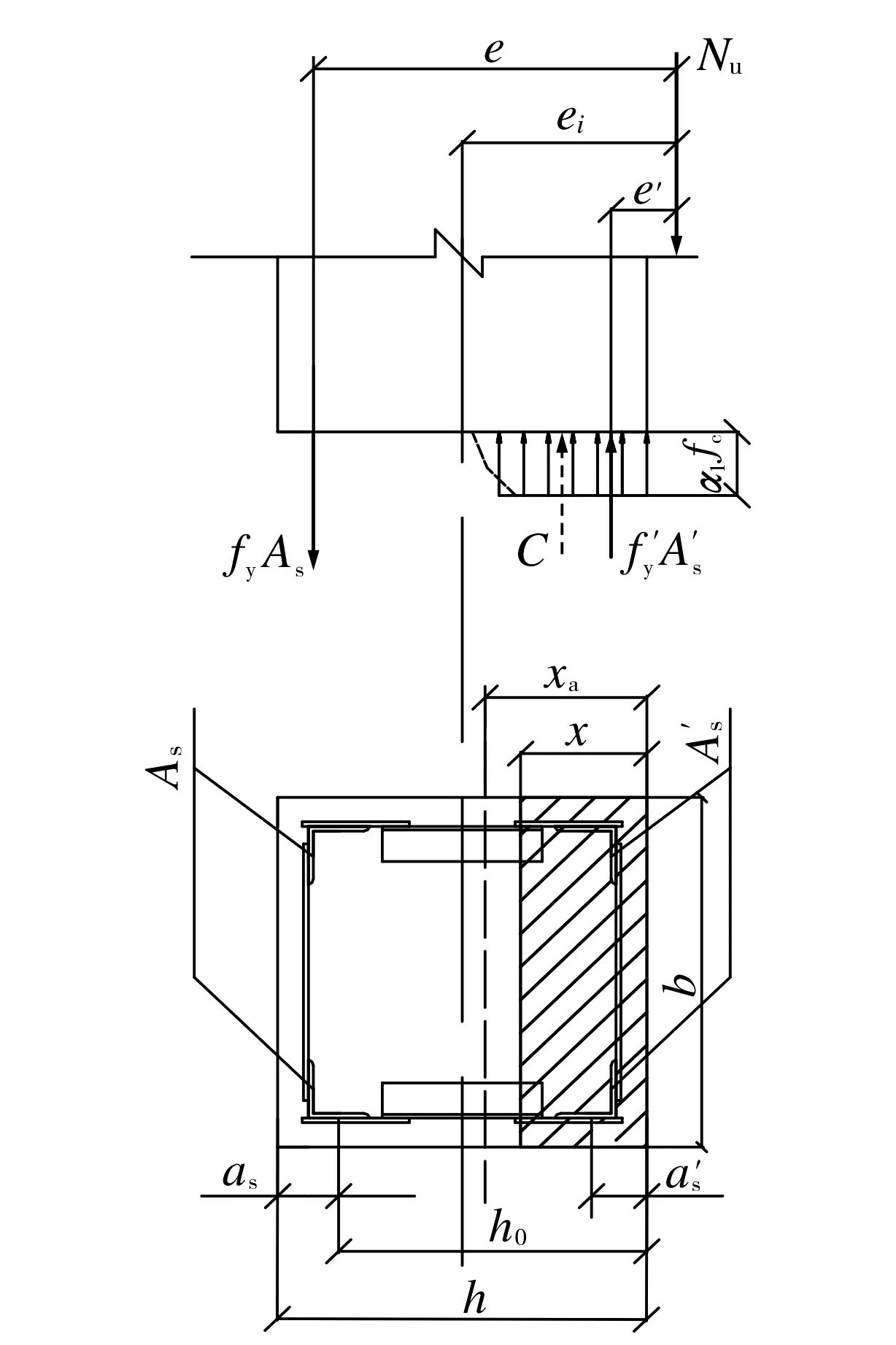
图10 矩形截面大偏压受压承载力计算应力图形Fig.10 Calculation stress pattern of bearing capacity under large eccentric compression of rectangular section

通过试验分析可知, 桁架式钢骨混凝土柱受拉区角钢先达到屈服强度, 然后受压区混凝土被压碎,受压区混凝土曲线应力图形可用等效矩形应力图代替, 如图10所示．由图10可知, 平衡条件轴向内外力之和及受拉角钢合力点的力矩之和均为0．桁架式钢骨混凝土偏压柱承载力荷载Nu=λ1α1fcbx+f′yA′s-λ2fyAs,Nue=λ1α1fcbx(h0-x/2)+f′yA′s(h0-a′s),e=ηei+h/2-as, 其中λ1和λ2为强度增大系数,根据试验数据线性回归得到λ1和λ2分别为2.78和4.19;α1为受压区混凝土矩形应力图应力值与混凝土轴心抗压强度设计值的比值;fc为混凝土轴心抗压强度设计值;b为矩形截面宽度;xa为截面实际受压区高度;x为等效矩形应力图受压区高度;fy,f′y为普通钢筋抗拉和抗压强度设计值;As,A′s为受拉区和受压区纵向普通钢筋截面面积;e,e′为轴向力作用点至受拉钢筋As合力点和受压钢筋A′s合力点之间的距离;h0为截面有效高度;a′s为纵向受压钢筋合力点至受压区边缘的距离;η为偏心受压构件考虑二阶效应影响的轴向偏心距增大系数;ei为初始偏心距;as为纵向受拉钢筋合力点至截面受拉边缘的距离;C为混凝土压应力的合力．

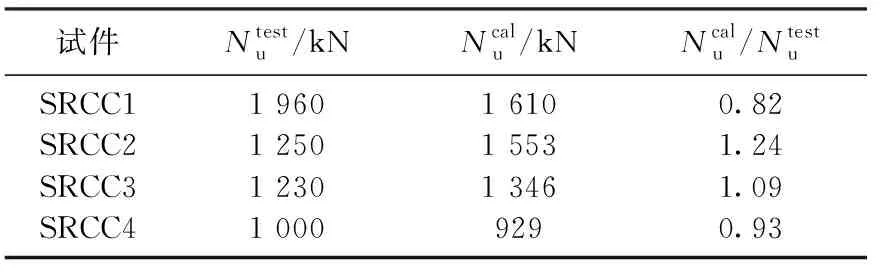
表4 大偏压柱承载力计算值与实测值比较