基于粒子群和布谷鸟搜索的BP神经网络优化方法研究

秦琪怡，郭承湘，吴帅，姚旭艺，陈宁江*，3

(1.广西大学计算机与电子信息学院，广西南宁530004；2.广西中医药大学网络和信息化管理办公室，广西南宁530200；3.广西多媒体通信与网络技术重点实验室，广西南宁530004)

0 引言

BP神经网络是基于梯度搜索技术寻找期望值与均方误差最小的多层前馈神经网络，依靠大量数据学习挖掘潜在规律以对未知事件做出合理假设与预测。BP神经网络算法基于结构优化和权重训练且具有强大的学习和搜索能力而被广泛使用[1]，但是传统的BP神经网络算法常伴有收敛慢、易陷入局部最优等问题[2]。对此，不少研究工作从不同角度探讨了通过结合智能规划算法来优化BP神经网络，例如：基于遗传算法的BP神经网络优化方法[3]，主要解决局部最优问题，但收敛速度较慢；基于粒子群优化算法(particle swarm optimization, PSO)的优化方法[4]，其前期收敛速度快，但迭代后期搜索能力较弱；基于布谷鸟搜索算法(Cuckoo search, CS)的优化方法[5]结合布谷鸟的巢寄生性与Levy飞行搜索机制实现高效寻优，全局搜索能力较强，但收敛速度较慢等。在当前不少实际应用领域中，例如产品安全风险预警应用[6]，仅使用传统的单一的BP神经网络或者简单融合智能规划算法的优化模型，仍在模型的寻优效率、准确率、稳定性等方面有提升需求，故近年也有将两种算法进行联合优化BP神经网络的研究工作[7-9]。粒子群优化算法与布谷鸟搜索算法均为群仿生智能算法，各自在全局搜索能力与收敛速度等方面有不同的表现：PSO算法前期收敛速度快，迭代后期搜索能力欠缺；CS算法全局搜索能力足，但收敛速度相对较慢[10]。

笔者对将粒子群算法和布谷鸟搜索算法融合的优化方法进行了探讨，提出一种分层的优化算法融合的MB-PSO-CS-BP模型，目标是减小BP神经网络初始化的敏感性，减缓其陷入局部最优的问题，最终提升预测效果。

1 MB-PSO-CS-BP模型

本文设计的MB-PSO-CS-BP模型如图1所示。该模型采用分层优化框架，下层为粒子群优化(PSO)模型，基于信息共享机制通过个体间竞争与协作相结合，用于BP神经网络算法前期搜索优化；上层的布谷鸟搜索算法(CS)计算鸟窝的适应度并基于Levy飞行机制改进鸟窝，找到全局适应度的最佳鸟窝结合，转化映射为BP神经网络对应的权值与阈值，能够较好地收敛于全局最优解。

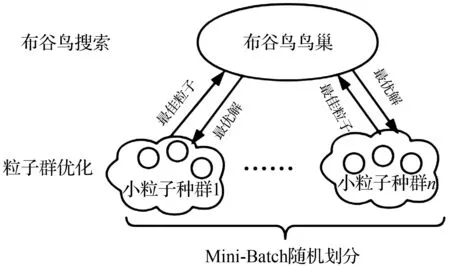
图1 MB-PSO-CS-BP模型框架Fig.1 Framework of MB-PSO-CS-BP model

BP神经网络算法的核心为梯度下降技术，在此方面尚需优化空间，对此笔者采用Mini-Batch批量计算[11]的方式提高模型训练效率。Mini-Batch算法是集梯度下降与随机梯度下降为一体，将数据集切割为多个小块计算的小批量梯度算法[12]，在减少计算量的同时能够减小梯度下降的随机性。打乱训练集与切分训练集是Mini-Batch梯度下降算法的核心步骤，训练集乱序示意图如图2所示。

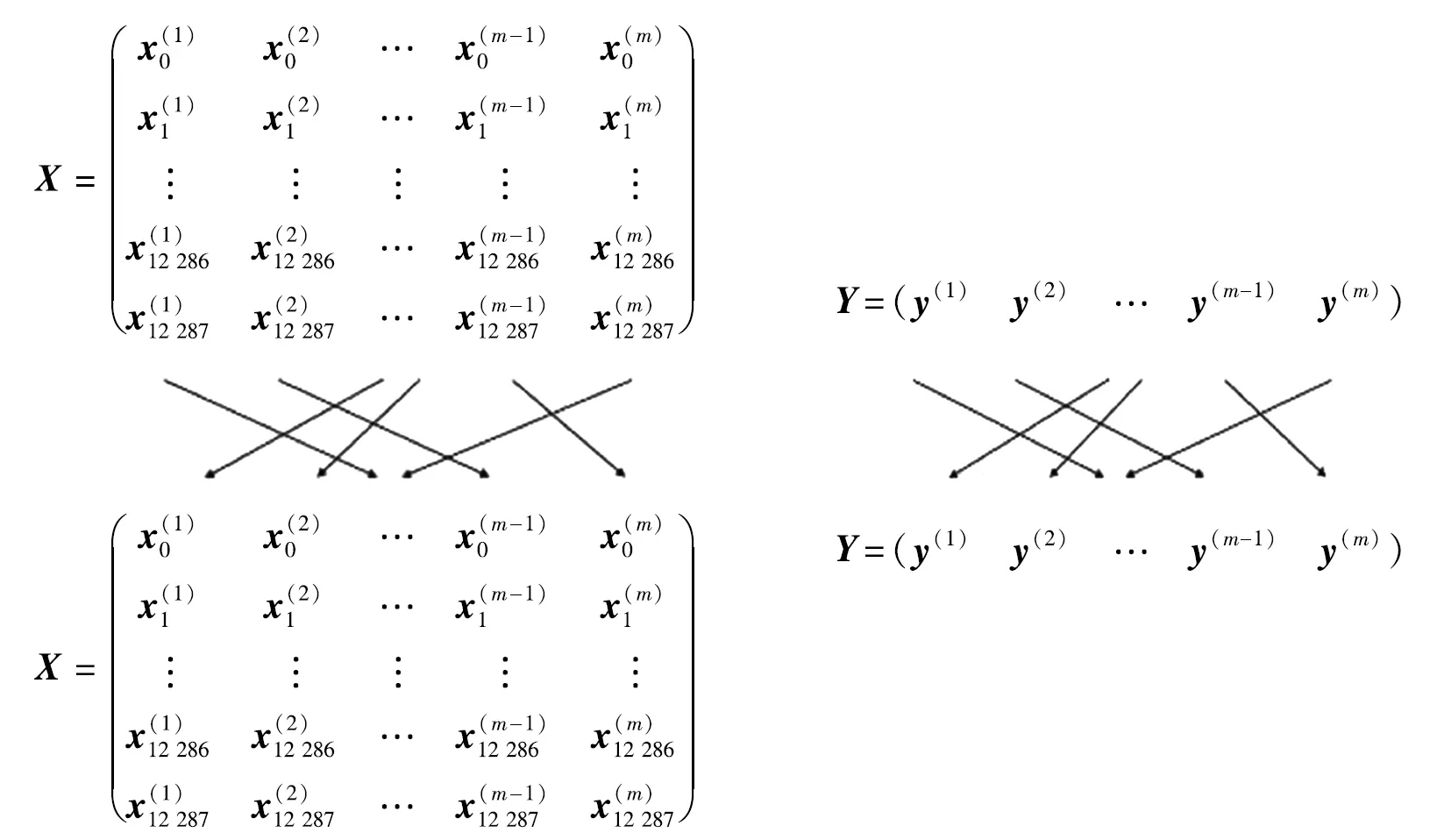
图2 Mini-Batch算法中的训练集乱序示意图Fig.2 Schematic of training set disorder in Mini-Batch algorithm

在图2所示例中，随机变换训练集顺序以确保样本被随机分成不同小批次，乱序过程中训练数据X与其对应的训练标签Y保持相对应。之后以2n为单位(本文将Mini-Batch的size设为64)切分乱序的训练集，切分为数个子集的数据集分别进行梯度下降，训练集切分示意图如图3所示。Mini-Batch梯度下降算法中的误差损失以上下波动的方式下降，总体为下降趋势，能够大幅提高训练效率。

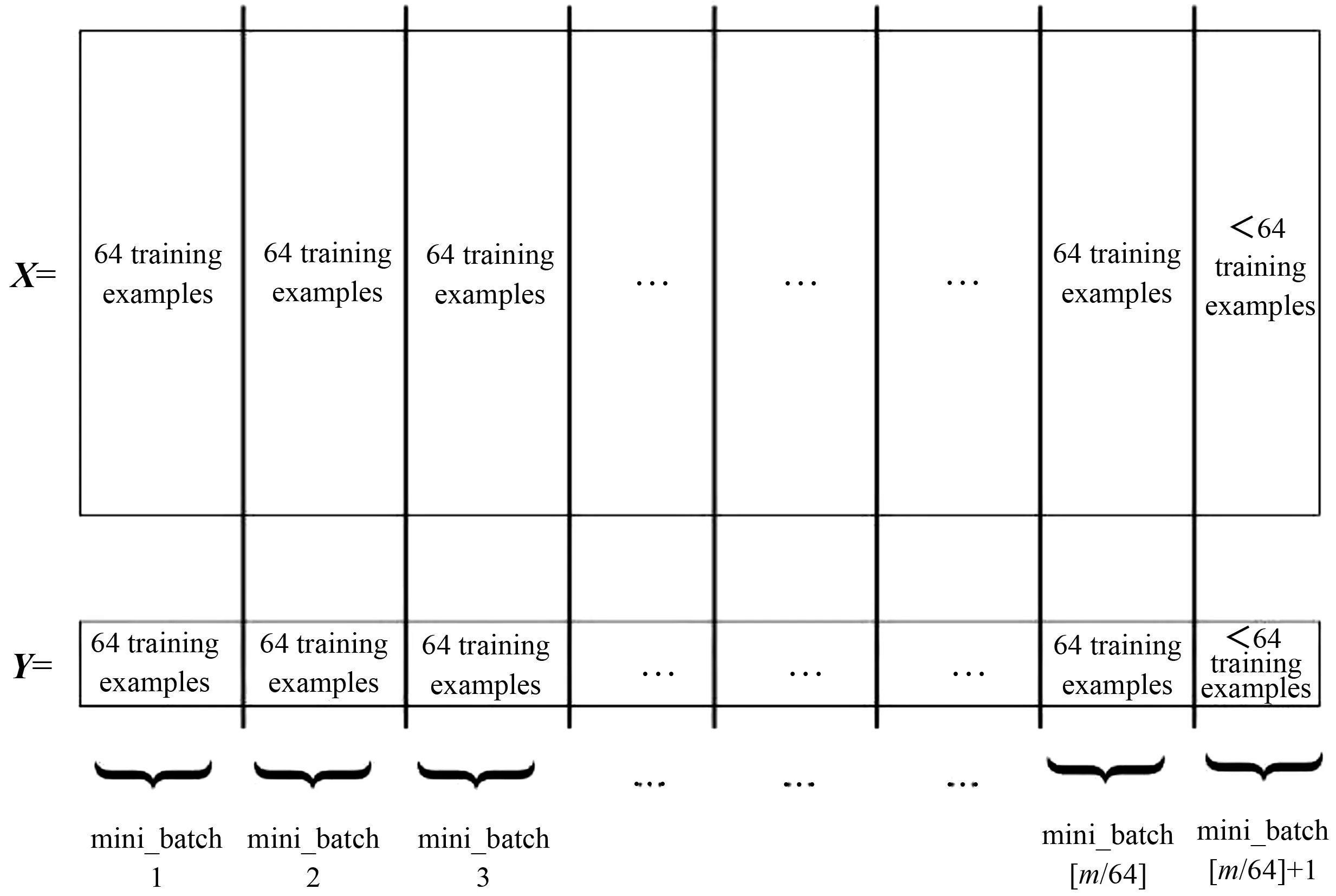
图3 训练集切分示意图Fig.3 Schematic of the training set cutting

综合以上，MB-PSO-CS-BP模型的基本思想为：随机生成2n个包含神经网络权值阈值信息的粒子，使用Mini-Batch算法将初始化粒子随机打乱顺序[13]，并按规则将粒子群分为多个小种群；下层运行PSO算法局部搜索的优势优化各小种群，将每个小种群求得的最佳粒子送到上层；上层运行CS算法进行全局搜索，进行深度优化，将求得的最优解返回到各小种群，将粒子群打乱重新分组；重复上述步骤。当符合终止条件时，将求得的全局最优粒子转化为BP神经网络初始化格式，进入BP模型继续训练。该模型的执行算法流程如图4所示。

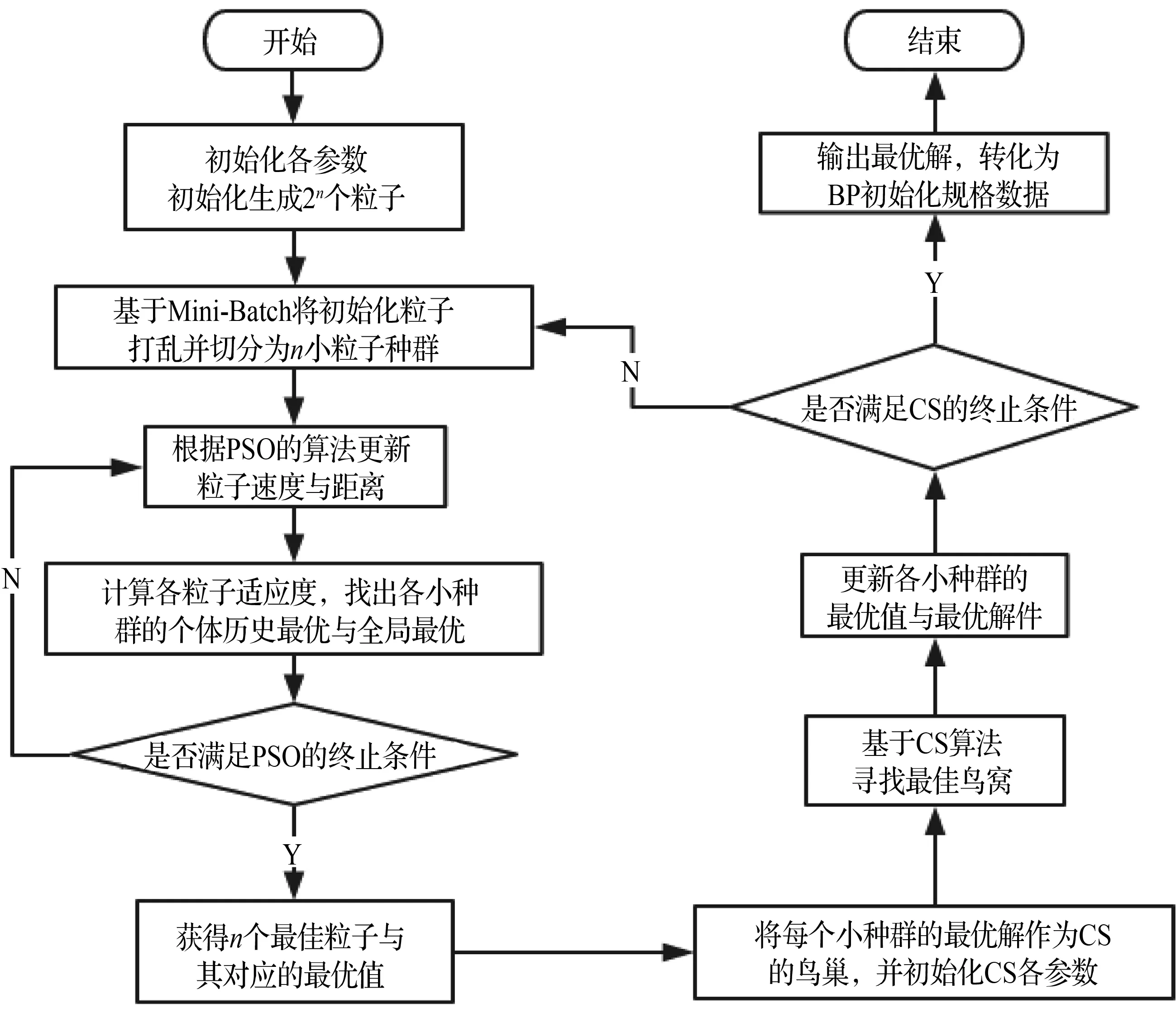
图4 MB-PSO-CS-BP算法流程Fig.4 Flow chart of MB-PSO-CS-BP algorithm

主要步骤说明如下:

Step 1:初始化BP神经网络的结构(本文设置BP神经网络结构为3层)，设其节点数分别为input、hid1、hid2、output。

Step 2:根据式(1)初始化2n个粒子，设置小种群个数为n，将适应度函数设置为BP神经网络的均方误差[1]，并初始化PSO算法中各参数，设置粒子个数及迭代次数；确定粒子搜索空间维度D，即单个粒子的规模，PSO中粒子维度与神经网络的连接节点的权值与阈值相映射，其中包含神经网络中所有的权值与阈值。D的计算如下所示：

D=input×hid1+hid1×hid2+hid2×output+hid2+output。

(1)

设置初始惯性权值ω、加速度常数c1和c2、随机初始化粒子群速度r1和r2，并基于抑梯度异常给定解空间范围[-bound,bound]，如下所示：

(2)

Step 3:使用Mini-Bacth算法将粒子群打乱，随机分为n个小粒子种群。

Step 4:计算各粒子适应度作为个体历史最优值，各小粒子种群的最优适应度作为小种群全局历史最优值，整个粒子群的最优适应度作为全局历史最优解。

Step 5:根据下述公式更新各粒子的速度与位置，并计算其适应度。

v(t+1)=ω(t)+c1×r1×(pbest-x(t))+c2×r2×(gbest-x(t)),

(3)

x(t+1)=x(t)+v(t+1)。

(4)

Step 6:将粒子当前适应度与个体历史最优值对比，若优则替换更新个体历史最佳粒子与个体历史最佳适应度。

Step 7:计算小种群的最优适应度，将其对应最佳粒子作为小种群最优解。

Step 8:计算大粒子种群最优值，与历史全局最优值比较，若优则更新替换全局历史最优值与全局历史最优解。

Step 9:判断PSO算法是否可终止，若可以则继续执行step 10，否则返回step 4迭代执行。

Step 10:将n个小粒子种群最优解作为CS算法的初始鸟窝，并初始化CS算法中各参数。

Step 11:计算各鸟窝适应度，并基于Levy飞行机制迁移鸟窝计算新窝适应度。将新旧鸟窝的适应度进行比较，若优则替代更新。鸟窝改进公式如下所示：

(5)

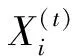
Step 12:CS算法优化最优解返回各小种群，与小种群历史最优解比较，若优则替代更新。

Step 13:判断是否符合终止条件，符合则执行step 13，否则返回step 3迭代执行。

Step 14:最后输出CS算法搜索的最优解，映射转化为BP的权值阈值用于后续的模型训练。

设粒子数为N，小种群数为n，PSO算法迭代i次，CS算法迭代j次，两层优化迭代m次，则MB-PSO-CS-BP的权值阈值初始化算法的时间复杂度为O(N×i×j×m)，该算法保留了PSO算法收敛速度快与CS算法全局搜索能力强的特点，但时间复杂度较高。

2 实验

2.1 实验配置

为验证MB-PSO-CS-BP算法的优化效果，与分别只用PSO和CS算法来优化BP神经网络的方法(分别记为PSO-BP、CS-BP)进行对比实验。实验是以某省食品药品监督部门提供的食品抽样检验数据为训练数据，使用BP神经网络进行预测食品安全风险。实验执行的软硬件环境基本参数为：CPU Intel(R) Pentium(R) CPU G640@2.80 GHz，8 GB内存，Python 3.7编程，操作系统为Win 10。

2.2 实验过程

在实验中提取两组数据集(分别命名为Dataset 1、Dataset 2)作为训练数据，数据集Dataset 1与数据集Dataset 2均从源数据中以2∶1随机抽取1 500条数据作为训练数据，从余下数据中随机抽取375条数据作为测试数据,分别在数据集上放入PSO-BP模型、CS-BP模型与MB-PSO-CS-BP模型各训练多次，从多个指标进行对比。有关实验参数设置如表1所示。

表1 实验参数设置Tab.1 Experiment parameter setting

2.3 结果与分析

基于数据集Dataset 1与Dataset 2进行训练模型，图5展示了各个模型在两个数据集上训练均方误差的变化。由图5可知均方误差在各模型上都呈下降趋势。PSO-BP模型在迭代600次左右收敛开始稳定，CS-BP模型的均方误差上下震荡非常大，PSO-CS-BP模型在迭代500次左右收敛趋于稳定。

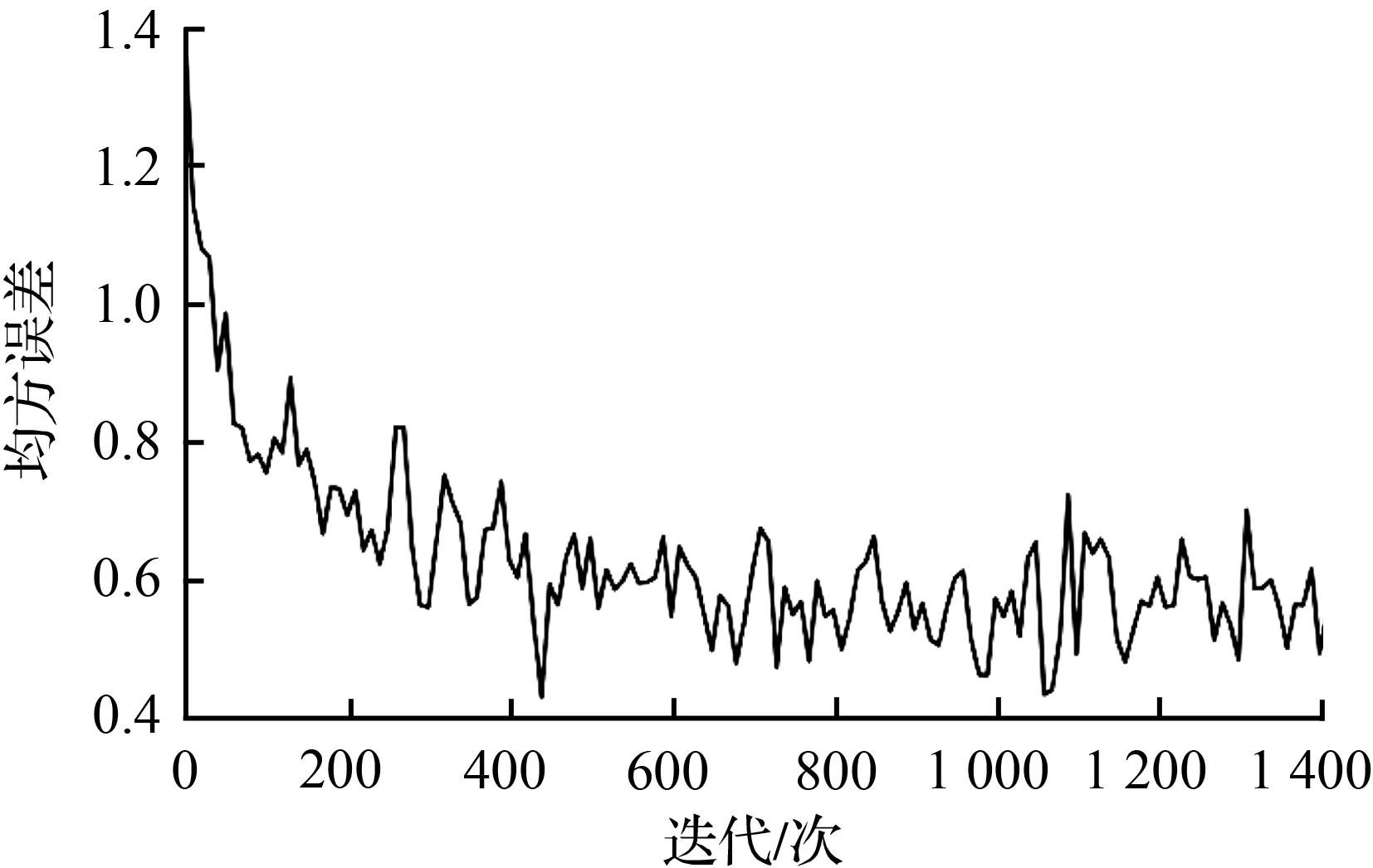
(a) Dataset 1的PSO-BP模型误差变化

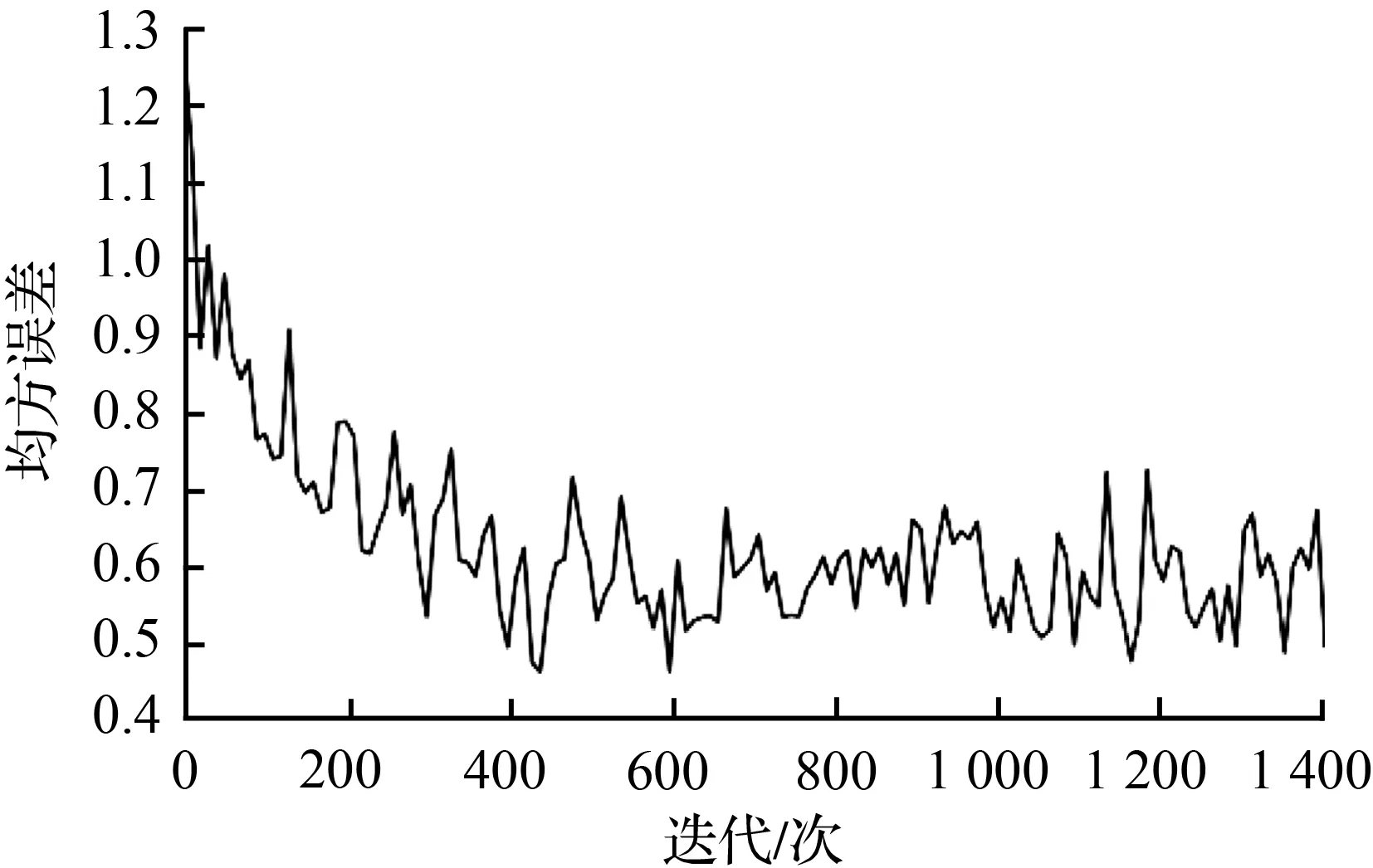
(b) Dataset 2的PSO-BP模型误差变化

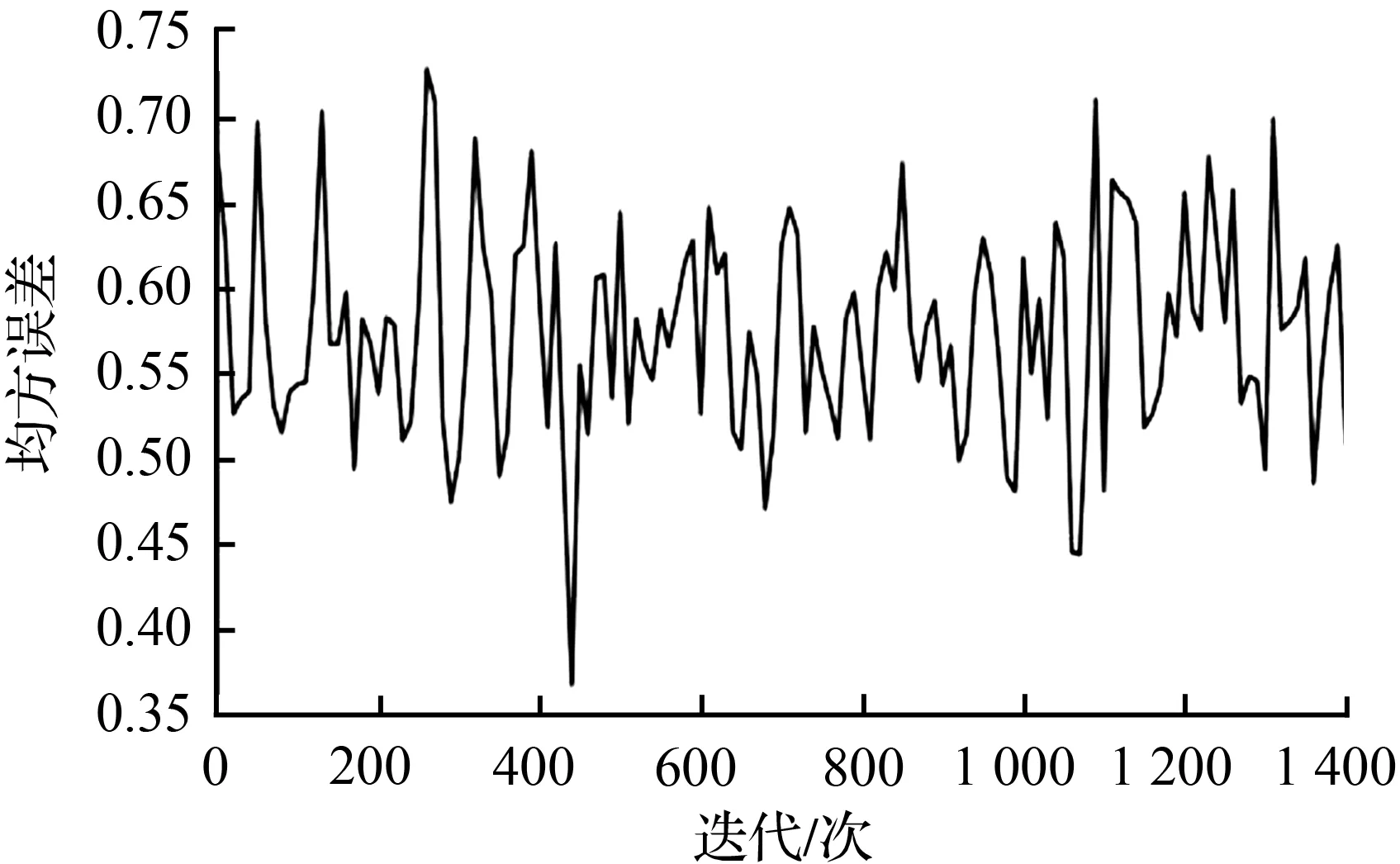
(c) Dataset 1的CS-BP模型误差变化

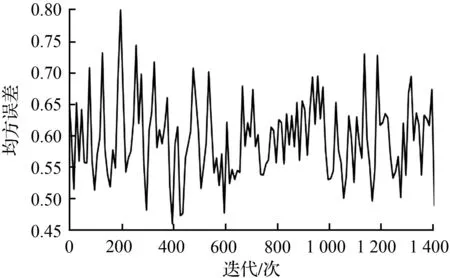
(d) Dataset 2的CS-BP模型误差变化

(e) Dataset 1的MB-PSO-CS-BP模型误差变化

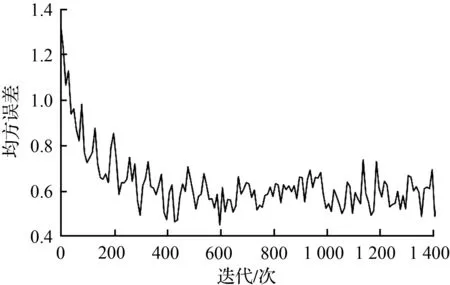
(f) Dataset 2的MB-PSO-CS-BP模型误差变化

表2和表3分别给出各模型在训练集Dataset 1、Dataset 2上的训练结果，列出实验的平均值。由表2与表3可见，经MB-PSO-CS-BP模型搜索的全局最佳粒子对应的全局最佳值，均小于其他模型搜索结果。从均方误差、准确率等维度的参数上可见该模型的性能更佳，一定程度上避免了BP神经网络陷入局部最小值，提高了模型精度。此外，从两组训练数据实验结果上来看，PSO-BP模型与CS-BP模型在不同数据集上的训练结果有优有劣，其训练效果并不稳定，模型使用者需经过多次训练模型择优选取较好的结果，而MB-PSO-CS-BP模型在不同训练集上均有不错的训练结果，且多次训练的结果较稳定。

表2 训练集Dataset 1的训练结果Tab.2 Training results of the training set Dataset 1

表3 训练集Dataset 2的训练结果Tab.3 Training results of the training set Dataset 2

表4给出了MB-PSO-CS-BP、PSO-BP、CS-BP模型特点比较。

表4 3种模型的特点比较Tab.4 Comparison of the characteristics of the three models

3 结语

本文提出了一种新的基于粒子群优化和布谷鸟搜索融合的BP神经网络优化模型，采用分层优化框架，将PSO用于底层多种群局部搜索，将CS用于顶层全局搜索，寻得的最优粒子转化作为BP神经网络的权值阈值的初始化，结合Mini-Batch算法，以克服收敛慢、陷入局部等不足。本文在实际数据集上进行了实验验证和对比，结果表明所提出的MB-PSO-CS-BP模型结合了PSO算法与CS算法的各自优点，缓解了BP神经网络陷入局部最小值的困境。下一步的工作将考虑使用基准函数等加强测试所提出模型的普适性，还可考虑分别在PSO与CS层次做进一步的深入优化以提高整体的性能。