高架简支梁桥柱式墩横桥向随机地震动响应

林桂武,葛新广,吴辉琴,李暾

(广西科技大学土木建筑学院，广西柳州545006)

0 引言

高架桥是一种能跨越河流、峡谷等障碍物并具有传力路线明确、施工简单、造价低的经济性桥型，且近年来随着城市立体交通的发展需要，城市高架桥也随着城市发展的需要大量涌现。然而，该类桥梁结构属于典型的“头重脚轻结构”，动力性能较差。1994年美国Northridge 地震导致数座桥梁倒塌；1995年日本阪神地震中，Hanshin高架桥全线路发生侧向倒塌[1]；2008年中国汶川大地震中在映秀镇附近一座高架桥桥梁因柱式桥墩剪坏发生数跨侧向倒塌或整体落地[2]。对近30年地震桥梁破坏情况调查统计，桥梁工程在每次大地震中都受到严重破坏，其中高架柱式桥墩因根部的破坏尤其严重。作为生命线工程的桥梁基于地震动的研究一直是广大工程人员的研究重点[2-6]。

桥梁地震动响应研究中，地震输入的选择至关重要，目前桥梁设计主要以地震动时程分析[4,7]和设计反应谱理论为主，随机激励下桥梁的地震动分析文献较少。然而地震动发生具有时间、空间及强度的随机性，而时程分析为确定性激励分析、反应谱理论为准静力分析，两者都与实际地震动存在明显的偏差。HOUSNER[8]于1947年提出用白噪声激励模拟地震动，开创了用随机激励研究结构地震动的先河。20世纪60年代，随着人类地震动时程记录的不断积累，日本学者KANAI[9]和TAJIMI[10]在对大量地震时程记录的基础上提出了过滤白噪声激励模型，工程上称之Kanai-Tajimi谱。该随机模型将基岩运动看做白噪声振动过程，其上覆盖土层看做过滤器，能根据场地不同来模拟地震动对地面运动的影响。虽然该模型过分夸大低频振动的影响，但仍能较准确的反应地震动的振动特性，是其他地震动随机激励模型的基础，受到广泛的应用[11-12]。

结构随机地震动响应的分析方法主要有频域法和时域法[12-13]。频域法中，因结构的动力响应与地震激励功率谱有直接代数关系而受到广泛应用，其中虚拟激励法[14]是其典型的代表。时域法是将结构的响应能表达成脉冲函数与地震动激励的杜哈梅积分形式，模态法是其典型代表，其中从解微分方程的角度，将二阶运动方程转为一阶运动方程而产生的复模态方法[15-16]具有能解决各类非时变结构的地震动响应的特点而得到广泛的应用。实际工程应用时，常需要获得结构的时域响应值；频域法应用时需要转换为时域值进而存在数值积分的复杂问题，虽然一些基于频域法的快速算法的提出[17]，对于复杂的地震动激励模型或者大型结构的响应分析频域法仍然存在计算效率低下的突出问题。此外，动力可靠度分析是结构抗震设计的关键问题之一，而结构响应谱矩是可靠度分析的基础，然而，目前计算谱矩的方法存在需要数值积分且计算量较大的问题。

本文以广西柳州某城市高架桥的多跨简支梁桥为研究背景，在侧向地震动作用下将其等效成4质点结构；地震输入采用Kanai-Tajimi随机谱，并利用其基于白噪声的过滤器微分方程，与桥墩运动方程联合组成非经典阻尼运动体系。利用复模态方法[13, 16]研究了随机激励下的质点位移、质点速度及质点间剪力的协方差分析。最后基于谱矩的定义，推到了桥墩各质点响应的0阶、1阶谱和2阶谱矩的解析解。

1 工程概况

广西柳州某城市高架桥，依据公路桥梁抗震设计规范，按7度设防。上部结构采用横向7片20 m跨度的简支小箱梁组成，一联7跨；桥墩采用采用边长为1.8 m的正方形的双柱墩，墩高20 m,采用板式支座。桥墩参数如图1所示：

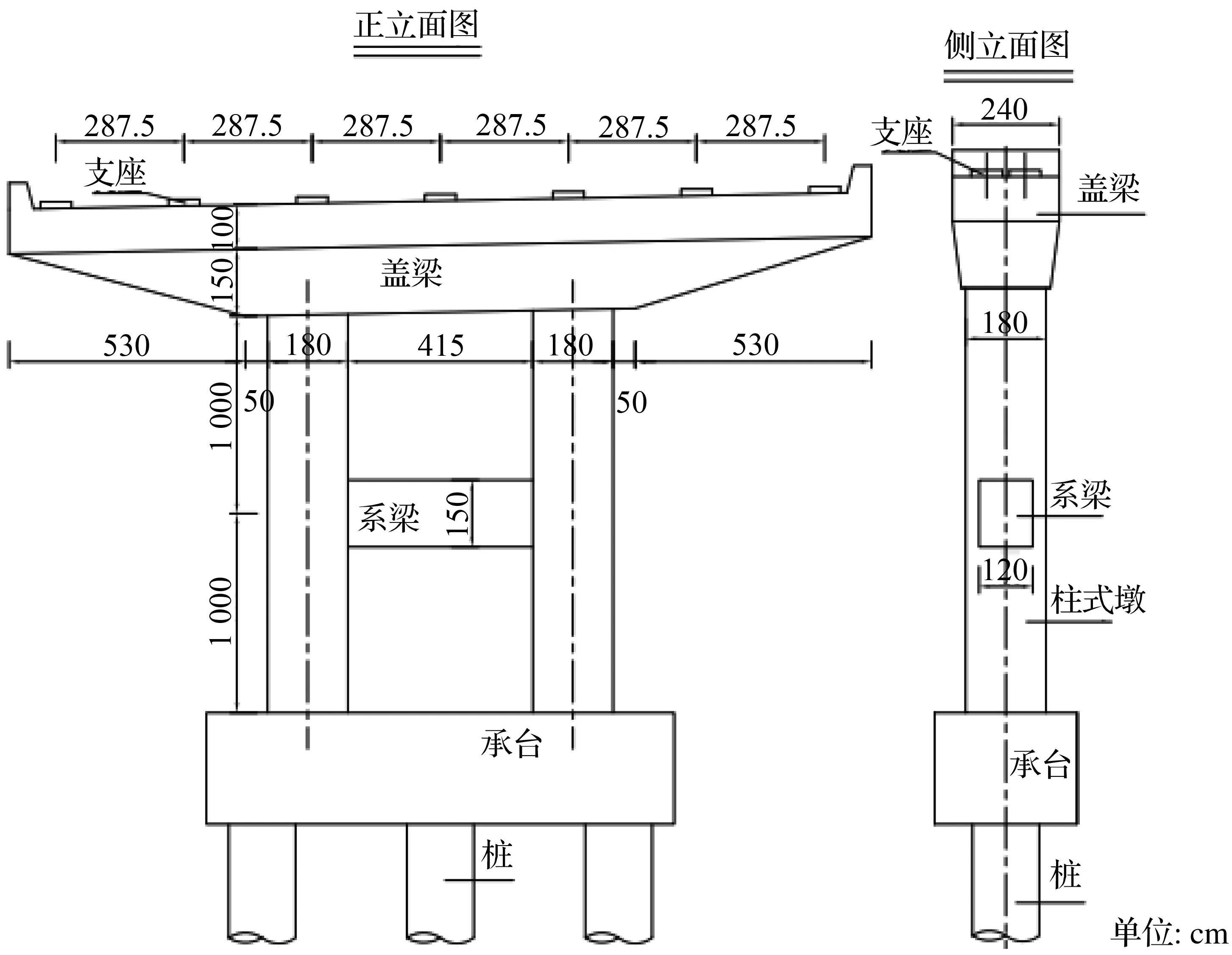
图1 桥墩构造图Fig.1 Structural diagram of pier

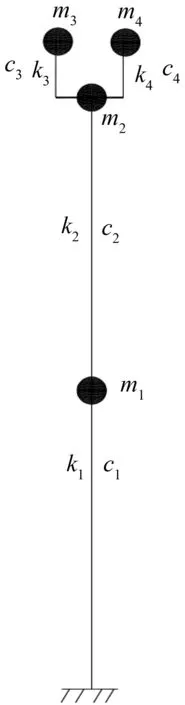
图2 桥墩计算简图Fig.2 Calculation map of pier

2 桥墩地震动运动方程

2.1 桥墩动力基本参数

根据结构动力学的离散原则，桥墩以系梁和盖梁为横向系，立柱为竖向系，其等效成双柱二横梁的框架结构，利用结构力学求出其横向抗侧刚度。根据系梁拉结作用，桥墩最后等效成如图2所示的m1-m2的2质点结构，集中质量分别取横向系和对应立柱的质量。桥墩采用钢筋混凝土，其阻尼按瑞雷阻尼由阻尼比计算，阻尼比取0.05。上部结构通过支座与桥墩盖梁相连，可等效成梁体质量、支座构成的振动体系；质点质量取20 m跨度简支梁的总质量的一半计；抗侧刚度k3,k4按照所采用支座的力学参数计算获得，根据支座的阻尼性能，由阻尼比来计算c3及c4，本文研究支座阻尼比对减震性能的影响，此处数值待定。结构振动基本参数见表1。

表1 结构振动基本参数Tab.1 Basic structural vibration parameters

2.2 桥墩地震动方程

由动力学知识，质点m1的运动方程：

(1)

质点m2的运动方程：

(2)

质点m3的运动方程：

(3)

质点m4的运动方程：

(4)

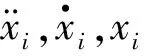
(5)

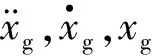
(6)

式中，S0为地震动强度常数，δ(τ)为Dirac函数。

地面运动的绝对加速度与Kanai-Tajimi谱的关系：

(7)

令：

(8)

联立式(1)～(5)及式(7)，桥墩运动方程表示为：

(9)

3 桥墩各质点动力响应的统一表达式

引入状态变量：

(10)

方程(9)改写为：

(11)

式中:

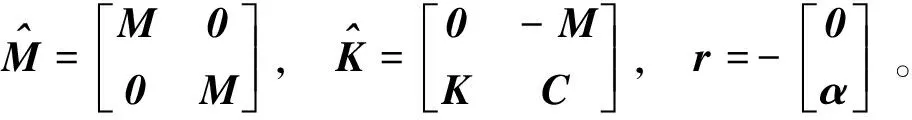
依据复模态理论[16]，方程(11)存在特征值矩阵P，右特性向量V、U,且特征值矩阵P为实部为正值的对角阵，上述参量支架存在关系：

(12)

引入复模态变换[16]：

y=Uz,

(13)

式中，z为复模态广义变量。

将式(15)代入式(11)并利用正交性，式(11)变为：

(14)

把式(12)代入式(14)，并整理为：

(15)

鉴于P为对角阵，则式(15)有分量形式：

(16)

式中，zi,ηi,pi分别为z,η,P的分量。

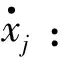
(17)

(18)

式中，uj为右特征向量矩阵的第j行向量，桥墩各个质点处响应的强度系数：

λj,i=uj,iηi,

(19)

式中，uj,i右特征向量矩阵的第j行第i列元素。

由结构力学理论并根据结构计算简图2可知，桥墩质点间的剪力为：

Vi=ki(xi-xi-1)，i=1～2,

(20)

式中，Vi表示桥墩第i质点与i+1质点之间的剪力。

对式(20)求导，可获得剪力的变化率：

(21)

同理，支座剪力及其变化率为：

V3=k3(x3-x2)，V4=k4(x4-x2),

(22)

(23)

根据式(17)、(22)，剪力可统一表示为：

(24)

根据式(18)、(23)，剪力的变化率可统一表示为：

(25)

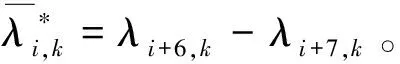
为后文推导方法，由式(17)、(18)及式(24)、(25)可知，桥墩质点处的位移及速度、质点间剪力及其变化率响应可统一表示为：

(26)

式中，l代表响应量，其第i个响应分量为：

(27)

式中，各响应的强度系数sl,i。

4 桥墩质点响应分析

4.1 响应协方差分析

由式(26)及随机振动的协方差定义[16]，响应Sl的协方差为：

(28)

由式(27)、(28)中的分量可表示为：

(29)

把式(6)代入式(29)：

(30)

利用Dirac的函数性质，式(30)改写为：

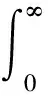
(31)

对式(31)积分：

(32)

由式(28)、(32)，基于Kanai-Tajimi谱的桥墩动力响应协方差为：

(33)

令：

(34)

则桥墩响应的协方差可表示为：

(35)

从式(47)中可知，桥墩基于Kanai-Tajimi谱的动力响应的协方差等于桥墩各个动力特征值所对应的指数函数的线性组合。因此，可以认为，多自由结构响应的协方差可转化为其振动特征值对应的协方差的线性组合，且表达式非常简洁。

4.2 响应谱矩分析

根据Wiener-Khinchin关系[16]，桥墩l响应的单边功率谱为：

(36)

式中，GSl(ω)为桥墩质点响应的单边功率谱。

把式(35)代入式(36)：

(37)

对式(37)进行积分：

(38)

由谱矩的定义[16]，谱矩αS,i可表示为：

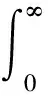
(39)

由文献[17],质点响应0阶谱矩、2阶谱矩与响应的协方差存在如下关系：

(40)

(41)

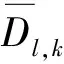
质点响应1阶谱矩的分析，把式(38)代入式(39)并取l=1，得：

(42)

对式(42)积分：

(43)

根据文献[17]可知，

(44)

则谱矩αSl,1可表示为：

(45)

由式(40)、(41)、(45)可知，结构动力响应的0-2阶谱矩均有解析解，且表达式简洁明了，与虚拟激励法[19-20]所提方法相比，本文方法不需要积分，计算效率大大提高。

5 参数分析

桥墩按7°设防，场地土为中硬土，其Kanai-Tajimi谱的参数为ξg=0.8,ωg=16.5rad/s,S0=0.006 9 m2/s3，对以下问题进行分析：

①支座阻尼比为0.05时,桥墩复振动特征值及对应的强度系数。

根据文中式(12)计算出桥墩的地震动复振动特征值，共10个，且两两共轭，共轭对的模值是相等的，为此共轭对按1个模态合计，计5个模态；按特征值模值从小到大进行排序，分别称之为模态1至模态5。根据复模态理论可计算模态1至模态5对应的强度系数，计算结果如表2。

由表2可知，模态3的等效阻尼比0.8，自振圆频率为16.5 rad/s，与Kanai-Tajimi滤波器的场地特征值与阻尼比一致，这是由式(5)本身能解耦为2个一阶微分方程的原因；模态3的强度系数的实部与虚部均比其他模态值大，说明地震动激励的振动作用在各个模态中其主导作用。模态1及模态4的强度系数也较大，但模态1及模态2特征值模值相差不大，但模态2强度系数很小，原因不明。

表2 各模态特征值及强度系数Tab.2 Vibration mode number, eigenvalue and modal strength coefficient

②支座阻尼比0.05时,桥墩位移及剪力的谱矩计算。

利用本文公式(40)、(41)及(45)计算桥墩各质点位移及剪力的0-2阶谱矩如表3、表4。

表3 质点位移谱矩Tab.3 Mass displacement spectrum moment

表4 质点间剪力谱矩Tab.4 Spectrum moment of shear forces

③支座阻尼比对桥墩侧向变形及剪力的影响。

阻尼是耗能的，因此需要分析桥墩支座的阻尼对桥墩侧向变形及桥墩内力的影响。为此，分别就桥墩支座阻尼分别取0.05、0.1、0.15、0.2、0.25工况下的位移和质点间剪力进行对比分析，如图3和图4所示。

从图3和图4可见，随着桥梁支座阻尼比的增加桥墩各质点的位移及各质点间的剪力明显减小。因此，支座阻尼对于桥墩抗震效果影响明显。桥梁设计时可采用大阻尼的支座可有效减震。

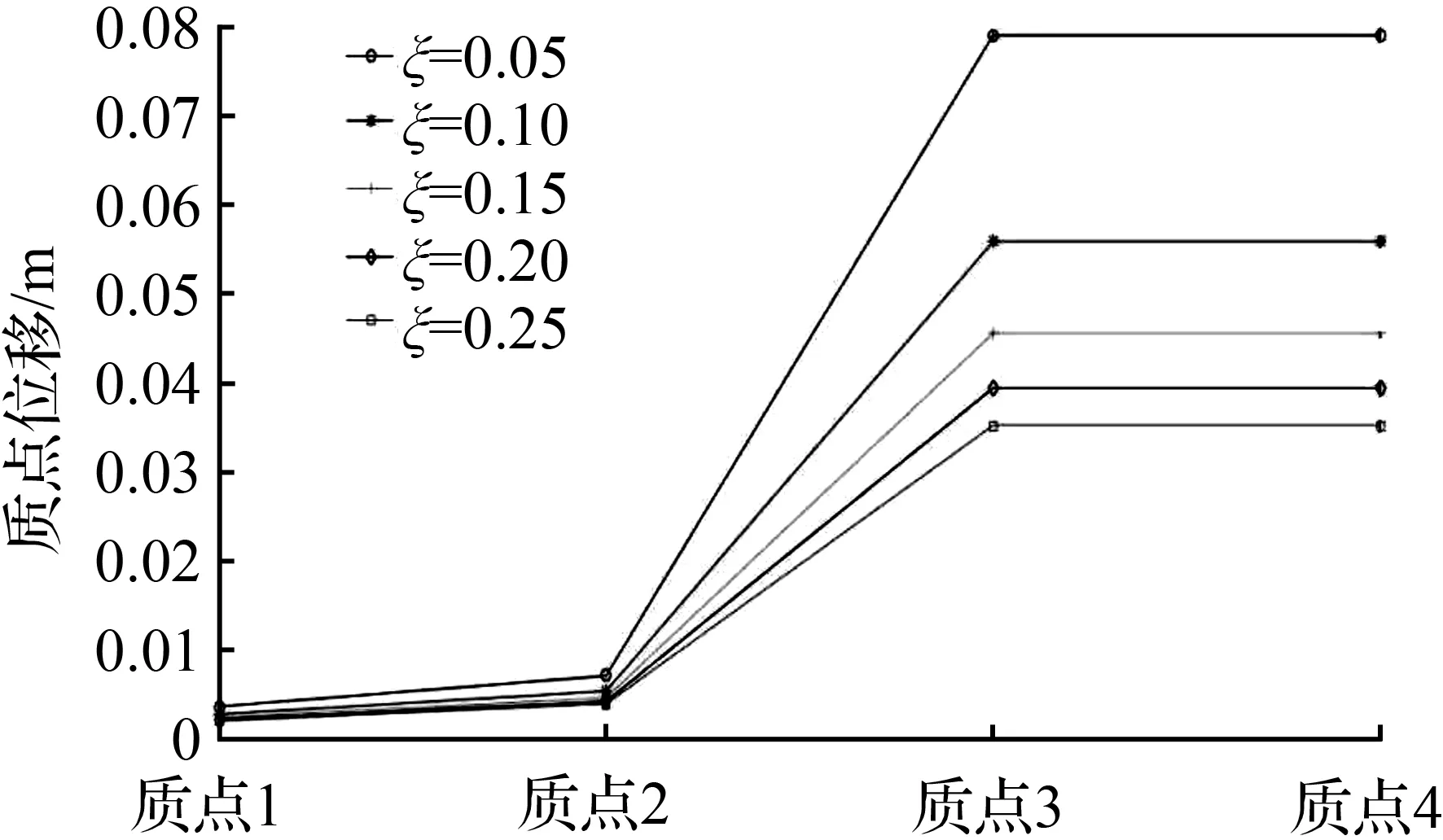
图3 桥墩各振动质点位移方差与桥墩支座阻尼比关系Fig.3 Relation between variance of displacement of vibration masses and damping ratio of pier support

图4 质点间剪力随支座阻尼比变化Fig.4 Relation between variance of shear force of vibration masses and damping ratio of pier support

6 结论

本文通过对一高架桥柱式的桥墩在Kanai-Tajimi随机地震动下的动力响应进行分析，结合Kanai-Tajimi滤波方程提出了该随机激励下响应、谱矩等振动特征的简明解析解，并分析了支座阻尼比对桥墩减震的影响，取得如下结果：

①利用随机振动理论对桥墩基于随机地震动激励下的振动响应分析，可较准确的描述实际地震动桥墩的动力响应，为桥梁基于抗震性能设计提供依据。

②将Kanai-Tajimi谱的滤波方程与桥墩的动力方程联立求解，可将复杂的地震动激励模型精确转化为白噪声激励，能极大的提高计算效率。

③本文所提方法为时域法，能获得桥墩地震动响应分析的0-2阶谱矩的解析解，与虚拟激励法等频域法相比，无需积分，计算效率高。

④桥墩支座类型众多，对于抗震的桥梁应优先考虑阻尼比高的材料制作，可有效减少桥墩的剪力及弯矩，提高其抗震性能。