基于NMF-SVM模型的上肢sEMG手势识别方法

隋修武，牛佳宝，李昊天，乔明敏

天津工业大学 天津市现代机电装备技术重点实验室，天津 300387

1 引言

表面肌电信号（sEMG）是肌肉运动过程中各运动单元产生的生物电信号经肌肉纤维传到皮肤表层的微电信号的叠加[1]，运动神经通过协调不同运动单元实现目标动作，因此对表面肌电信号中蕴含的运动信息的解析有利于区分不同的运动模式。目前利用肌电信号对假肢进行控制的主要研究集中在基础层面，如林上耀等人利用ADS1198 对肌电信号进行128 路的高密度采集[2]，Joseph R K等人利用混合模型对肌电信号进行去噪[3]；Meng Q、杨大鹏、Nishad A等分别在时域、频域和时-频域对信号进行特征值的选取[4-6]；Li C 对反向传播网络进行优化，从而实现对假肢的控制[7]。虽然以上相关研究取得了良好的效果，但也同时存在一些问题。例如高密度信号采集导致的超高维数据处理速度延迟过高，模式识别的效果过于依赖分类器的选取且往往忽略肌肉间的协同而靠牺牲维数来增加信息量。

目前基于表面肌电信号进行动作识别的研究多是采用首尾连接的方式将各通道计算出的特征值堆叠起来，并没有考虑到各动作的形成是由不同激活程度的肌肉相协调完成的，同时若仅选取少量特征值又达不到应有的分类效果。本文通过组成规律性的特征矩阵并降维得到代表不同动作对应肌肉激活程度的系数矩阵进行分类，充分利用所提取特征之间的关联和肌肉的协同以提高信息的利用率。首先选取与目标识别动作关系密切的上肢肌肉进行肌电信号的采集并计算特征值之后，利用本文提出的特征值排列规则组成特征矩阵，运用非负矩阵分解将特征矩阵在保留运动信息的前提下进行降维分解，进而利用支持向量机对分解信息进行训练和识别。本文还比较了传统SVM 分类器的分类效果，结果证明特征矩阵的构建较好地解决了信息量与维数之间的矛盾。本文将按照如图1的思路展开研究。

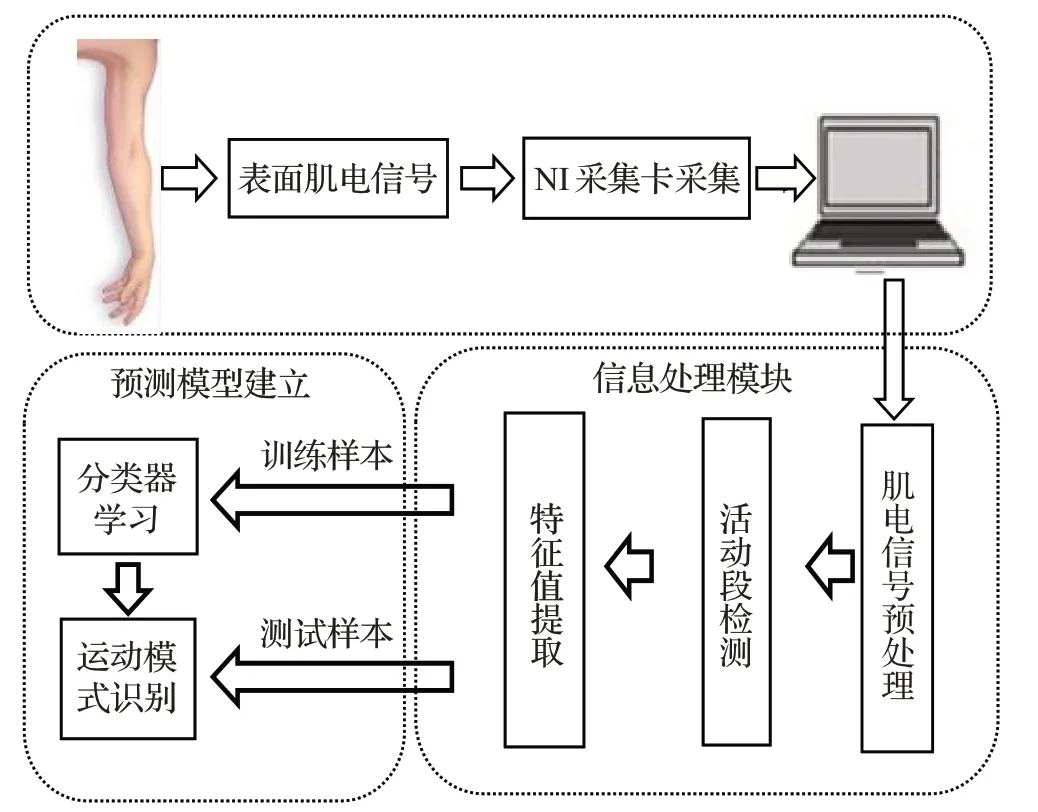
图1 基于sEMG的动作识别模型原理图

2 实验数据采集及预处理

2.1 实验数据采集

实验对象均为右利手且无上肢运动功能障碍或关节损伤病史。其中男性4名：年龄为23～25岁，体重55～75 kg，身高160～181 cm；女性4 名：年龄为23～25 岁，体重42～54 kg，身高152～175 cm。所有受试者均自愿参加此测试，受试前24 h 内未作剧烈运动，以满足实验要求的非疲劳条件。

实验采集采用埃力智能科技有限公司TB0820表面肌电仪对肌电信号进行采集，采样频率为1 000 Hz，仪器内置截止频率2 000 Hz 的低通滤波器和截止频率为10 Hz的高通滤波器。记录两种手部动作和四种腕部基本动作方式，其中手部动作包括握拳和张手，腕部动作包括屈腕、抬腕、腕左旋、腕右旋。采样频率为1 000 Hz，采用贴片式一次性生物电极片采集表面肌电信号，采集片应顺着肌纤维方向粘贴。采集前先用酒精擦拭采集部位，去除皮肤表面油脂和皮屑。采集过程中记录受试者的编号、信号采集开始时间、运动状态等信息。由于手部和腕部的运动多与前臂肌肉群的尺侧腕屈肌、指浅屈肌、掌长肌及指伸肌有关，因此本实验主要选取以上四块肌肉进行采集，采集的具体位置如图2所示。

图2 上肢表面肌电采集位置

2.2 信号预处理

实验对象正坐且两手臂自然下垂，受试者每个动作重复进行，一组动作完成后受试者有5 min休息时间，每种动作各采集20 组，同种动作做完后受试者有足够的休息时间。由于肌电信号频率范围在20～1 000 Hz且主要能量集中在50～150 Hz[8]，因此对信号进行截止频率为20 Hz的巴特沃斯二阶高通滤波，截止频率为500 Hz的巴特沃斯二阶低通滤波，以及50 Hz的工频陷波。

表面肌电信号由于其微弱性，易受到电路及外界环境的干扰，其中以工频干扰、基线漂移、白噪声等干扰最为严重[9]。而仅仅利用采集装置的滤波功能达不到对白噪声的降噪，本文根据肌电信号的特点利用非线性小波变换阈值法对信号进行滤波。首先用正交镜像滤波器（QMF）对信号进行滤波后得到噪声信号的小波系数ω，之后利用非线性函数y(ω)=sign(ω)(|ω|-t)作用于数据，并根据设定变阈值，由此给出小波系数的估值，其中σ为噪声强度。再设置一个信号能量阈值，将大于等于此阈值的小波系数等于0，然后进行小波反演重建，进而获得信号f(t)的估值[10]，其滤波前后对比如图3所示。

从滤波前后的频谱对比图4 可以看出带通、带阻、陷波器和非线性小波变换阈值滤波可以有效地将电路以及外界干扰产生的大部分噪音去除，同时由直流电路产生的干扰分量也被完全清除。

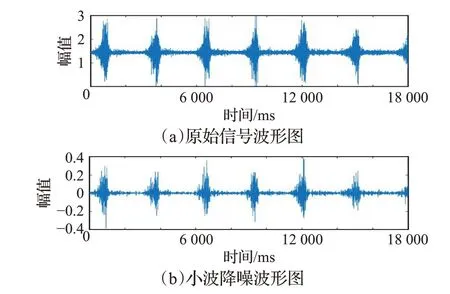
图3 滤波前后信号对比图（握拳）

图4 降噪前后频谱对比图（握拳）

2.3 活动段检测

肌电信号一般可分为静息信号和活动信号[11]，静息信号常伴随着人体的背景噪声信号，平均能量低；活动信号为肌肉运动时产生的生理电信号，平均能量高；静息信号和活动信号波形特点有明显的不同，前者变化较为缓慢，而后者在幅度上变化剧烈。本文采用双门限检测法利用短时能量和过零率两个特征进行端点检测。根据信号设置能量阈值、TL、TH和过零率阈值ZCR，当其中一路的某帧信号大于TL或者大于ZCR时，即认为信号的开始起点，当大于TH时，则认为正式的活动信号，如果保持一段时间，则确认这段信号即运动信号。

图5 肌电信号活动段检测

根据此方法对握拳动作的尺侧腕屈肌的肌电信号做端点检测分析，其结果如图5 所示，红线表示通过双门限检测法检测出的肌肉活动段肌电信号，可以看出做出握拳动作的两段信号均被正确识别出。经实验测试该方法监测的有效率为95%，部分监测失误主要为肌肉疲劳引起的背景噪声过大所致，该方法满足了实验需要。

3 特征值及特征矩阵的计算

肌电信号的特征值种类可分为五大类：时域特征、频域特征、时频域特征、基于非线性分析特征和基于参数模型的特征[12]。本文选取了时域中的均方根值(RMS)、频域中的中值频率(MF)以及时频域中的三级小波包系数方差最大值(Emm)、小波包系数能量最大值(VARmm)作为特征值。以上四种特征值计算方法如下。

均方根值能够反映肌电信号振幅变化，常被用于实时地、无损伤地反映肌肉活动状态，具有较好的实时性。其计算方法如下：

其中，n代表信号的长度，x代表信号值。图6 为由肌电信号计算得到的均方根变化图。

图6 sEMG和RMS信号示意图

中值频率反映了信号的不同频率分量的变化，其计算公式为：

其中，Psd(f)为功率谱密度估计函数。

建立在小波分解基础上的小波包变换是一种基于完整二叉树结构的信号分解与重构算法[13]。它对肌电信号的子空间的低频部分和高频部分同时进行分解，提高了其时频分辨率，是一种精细的信号分析方法。小波包系数的计算为：

其中，h(m-2l)和g(m-2l)是尺度p下的两组函数，p代表级数。

在经过3层小波包变换后，原始肌电信号f(t)被分解成为8个不同的频段分量，如图7所示，取分解得到的小波包系数的能量(Emm)和小波包系数的方差(VARmm)，然后对两项指标分别取最大值。分解结果不仅可以反映原始信号的频域细节信息，而且通过分解系数重构的信号叠加后和原始信号保持一致，充分体现了分解系数对原始信号信息的还原能力。因此提取不同动作模式下肌电信号的小波包分解系数作为特征，可以为多样性模式辨识提供良好的条件。

图7 3层小波包分解树

计算得到以上四种特征值后，本文提出了一种特征值的组织方式，即按照行代表示肌肉类型，列代表特征值类型的规则，对提取的四路信号特征值进行排列组织，即可得到实验所需4×4维的特征矩阵。如表1为对握拳动作信号提取特征值后按照上述排列要求组成的一组特征矩阵。

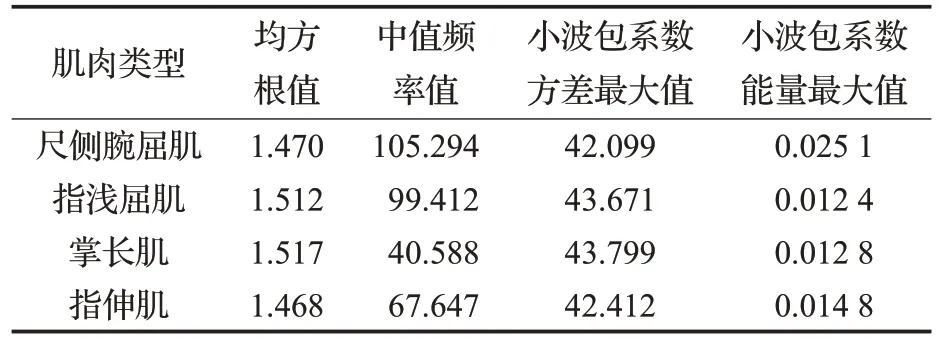
表1 握拳动作特征值排列组成的特征矩阵

这种特征值的组织方法不仅可以存储肌肉的运动信息，且保存了运动过程中肌肉的协同作用，在所选能够代表运动类型的有限的肌肉前提下最大限度还原了完整动作在时域、频域以及时频域的内在联系以及肌肉配合。

4 NMF-SVM模型建立

本文对上述组成的特征矩阵进行降维以降低计算成本以及满足实时性识别的要求。非负矩阵分解具有占用存储空间少、分解形式和分解结果的可解释性以及实现的简便性等优点，刚好满足实验快速准确的要求。且特征矩阵的元素均为非负数，也符合运用非负矩阵分解的前提条件。

为了达到降维且便于分类器训练识别的目的，将上述组成的4×4 维的特征矩阵分解为一个4×1 维和一个1×4 维的矩阵的乘积，即n=4,r=1。为了确保分解得到的矩阵包含原矩阵的运动信息，需要对分解的过程进行优化。分解过程中W、H的初始值是随机的，由于残差优化目标D可能存在局部最小，所以不同的初始W、H值可能会得到不同的分解结果。非负矩阵分解通常有两种更新规则，分别是交替最小二乘法和乘性更新法[16]，其中前者的收敛速度更快且相对稳定而后者对初始值较为敏感，因此可以先利用乘性更新法从多个初始值估计W、H，再用交替最小二乘法从前者估计的W、H中寻找更优结果。更新计算方法如下：

步骤1分解得到的矩阵与原矩阵之间的噪声可表示为：

其中，V表示原矩阵，W表示分解后的基矩阵，H表示分解后的系数矩阵。

步骤2为保证分解的精度，需要寻找WH使||E||最小，这里引入损失函数D(V,WH)，即分解模型可表示为优化问题：

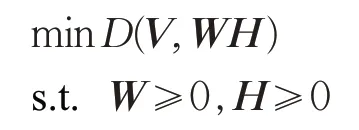
则目标函数可表示为：

步骤3假设||E||符合高斯分布，那么可求得最大似然函数：

步骤4通过迭代计算，得到多组初始系数矩阵W和基矩阵H。

步骤5再利用交替最小二乘法计算最优解，为了规避过拟合等问题，使优化问题正则化，目标函数可表达为：

其中λ是正则化项的系数。

步骤6先固定H，将损失函数D(W,H)对Wi求偏导，令倒数为0，得到：

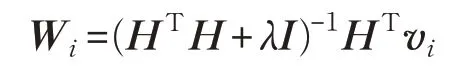
同理固定W可得：

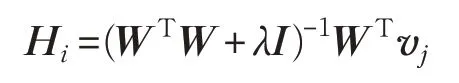
其中，vi是V的第i行，vj是V的第j列，I是单位矩阵。

步骤7通过对乘性更新法得到的多组初始矩阵分别进行多次迭代优化，得到损失函数最小时的系数矩阵W和基矩阵H。

通过非负矩阵分解将由肌电信号特征值组成的4×4 维特征矩阵降维为包含肌电信号肌肉间内在联系的1×4维的基矩阵与4×1维的系数矩阵的乘积，以降低分类器的学习训练时间与计算复杂度。

将六种动作的特征矩阵降维后得到的系数矩阵送入到分类器进行训练，实验选取了支持向量机作为动作识别实验的分类器。

支持向量机是针对小样本学习问题而提出的一种新的机器学习方法，其较好地解决了以往机器学习模型的过学习、非线性、维数灾难以及局部极小值等问题，具有较好的泛化能力[17]。然而，该方法在大规模训练样本时，同样存在训练速度慢、稳定性差等缺陷，因此通过上述的非负矩阵分解方法将样本进行降维大大缓解了训练的复杂度，能够有效解决支持向量机的局限性。

由于支持向量机最初是为二值分类问题设计的，当处理多类问题时，就需要构造合适的多类分类器。本文采用“一对一法”对六类动作进行分识别，分类器的个数G可由公式计算：

其中k为需要识别的类别数。

5 实验与结果分析

实验将从两方面对所提模型进行分析：（1）为验证模型的有效性，将利用相同样本信号对NMF-SVM模型与传统SVM 进行对比实验。（2）为判断模型的识别性能，将训练样本与验证样本的数据来源分割开来用以实验，以评估方法的通用性。

利用支持向量机对降维后的特征矩阵进行分类，每种动作使用1 000组特征矩阵按照7∶3的比例参与分类器的训练和验证，训练和验证的样本不重叠且从实验者中平均调取。采用特异度、灵敏度、准确率作为识别效果的评价指标，将某一动作模式被正确判别为该模式的情况记为真阳性，将不属于某一动作模式被判别为不是该动作的情况记为真阴性，则特异度表示不属于某一类且被正确判定的概率，灵敏度表示属于某一类且被正确判定的概率，此处的灵敏度和准确率数值上相等，将分类效果通过混淆矩阵定量显示出来。

表2 所示为相同实验条件下NMF-SVM 模型与传统SVM 的对比实验结果，A 组实验为利用NMF-SVM模型进行的实验分类结果，混淆矩阵的每一行代表分类器对某一动作实际分类的标签分布，每一列代表原始标签样本被分类器判定的标签分布情况。例如，表2的第一行表示分类器对受试者男A 的300 组“握拳”动作的识别分布，其中292组被正确分类为“握拳”动作，5组被错误归类为“左旋”动作，3组被错误归类为“右旋”动作，分类器的灵敏度、特异度和准确率分别为97.3%、99.8%和97.3%。第一列表示标准的“握拳”动作样本中有292组被成功分类，另有1组样本被分类器错分入“左旋”模式，2组样本被错分入“右旋”模式。

表2 NMF-SVM模型与传统SVM动作模式识别结果统计

与B 组实验中传统SVM 的识别结果比较，统计结果表明：（1）实验对象的平均动作模式识别率在95.55%以上，各动作模式识别准确率普遍高于传统支持向量机。（2）识别模型对于各动作判别发生错误分类的样本主要集中在“左旋”和“右旋”动作。分析原因在于左旋和右旋动作涉及到尺侧腕屈肌、掌长肌的皮下滑动旋转，而表面贴片电极仅随着表面皮肤移动，两者之间发生较大相对位移，进而导致采集到的表面肌电信号混有来自于其他信号源的信号，因此在进行模型训练时左旋和右旋与其他动作的支持向量存在重叠的现象。

考虑到模型的通用性，即模型中参数的确定是基于提取了部分受试者肌电信号通过训练的，但模型的确立应对其他部分人同样适用。同时为了分析所提模型在相同被试和不同被试条件下的识别性能，实验设计了男女混合验证的方式以消除性别的影响，按照性别将实验对象划分为两组，其中男女组中分别随机抽两位的肌电信号作为训练信号，其余四位的肌电信号则作为验证信号。

表3 所示为训练与验证的数据分别来源于不同的实验对象，即训练样本与验证样本不相关。由表3的统计结果分析可知：（1）所提模型的平均准确率为95.0%，依然具有较高的识别率。（2）本实验对比表2 中实验训练样本容量小的情况下平均准确率仅降低了0.55%，说明由模型计算得到的各动作系数矩阵有较好的辨别性。（3）男女肌电信号样本实验的识别效果无明显差别，在训练样本足够的情况下，模型的兼容性良好。同时可以看出，各受试者在“左旋”和“右旋”动作的识别率依然较其他动作偏小，电极片与肌肉间的相对滑动是之后模型需要针对优化的一个重要方面。

表3 样本分离实验动作模式识别结果统计

本文采用的表面肌电信号采集仪的转换和传输延时小于2 ms；特征提取过程采用的是128个采样点的短窗，延时时间小于28 ms。特征的提取及降维算法简洁快速，单条特征向量提取耗时小于18 ms，基于SVM 的分类器分类时间小于5 μs/次，所以从表面肌电信号采集到模式识别输出的总延时小于150 ms。因此本文提出的方法可以满足主动康复训练和普通人机交互控制领域的实时性要求。

6 结论

本文对基于表面肌电信号形态特征的手部动作模式识别进行了研究，实现了手部的6种精细动作模式张手、握拳、腕屈、腕伸、腕右旋、腕左旋的识别。运用本文中提出的NMF-SVM模型，首先将从肌电信号中提取的高维特征值按照规则组成特征矩阵，再对其进行降维和识别，实验结果证明该模型较好解决了维数与时间成本之间的矛盾。

模式识别的输入特征值的选取兼顾了肌电信号的时域、频域以及时频域的特性，将特征值按照行表示肌肉类型，列表示特征值类型的规则，对提取的四路信号特征值进行排列组成特征矩阵，这种组织方式保留了运动过程中肌肉间的协同信息，利用非负矩阵分解对高维特证矩阵进行降维得到表示各肌肉对动作贡献率的基矩阵，以及表征各肌肉激活程度的系数矩阵。不但降低了分类器的训练时间成本，同时与普通SVM相比，达到了93%以上的准确识别率，其平均识别率提高了5.2%，识别效率提高了一半，具有实用价值。