基于《同义词词林》深度的词义相似度计算研究

杨 泉，孙玉泉

1.北京师范大学 汉语文化学院，北京 100875

2.北京航空航天大学 数学科学学院，北京 100191

1 引言

词语间的语义相似度（本文简称词义相似度）计算是自然语言处理中文本数据处理的基础，随着人工智能时代的到来，词义相似度计算越来越多地应用到机器翻译、人机问答、情感计算、信息抽取、生物医学等不同领域。

目前词义相似度的计算方法基本上可以分为两类：一类是根据某种已有知识本体（Ontology）或分类体系（Taxonomy）进行计算；另一类是在大规模语料库的基础上直接统计和计算[1]。基于语料库的方法需要在大规模精确标注语料的基础上进行，对语料的依赖性较大，可解释性也较差。而基于知识本体的方法依据人类的世界知识，对词语之间的语义相似程度进行计算，具有较强的理论依据。

国外很多词义相似度测量方法是使用WordNet 作为底层参考知识本体来实现和评估的[2]。例如Resnik等在WordNet 的“IS-A”分类体系基础上提出了一种基于共享信息内容概念的词义相似性计算方法。对同义词表组内的名词词义分配置信值，利用分类相似性解决语义歧义问题[3]。Taieb 等提出了一种基于WordNet 层次结构深度分布的相关概念下位词子图量化法。该方法对WordNet 中两个待比较词的下位词和深度参数比组成的子图进行量化，并利用与“IS-A”分类体系相关的拓扑参数，计算两个词语的语义相似度[4]。WordNet 是目前世界上计算英语词义相似度的主要知识本体依据。

国内中文词义相似度计算也有采用知网作为分类词典的方法，刘群、李素建等在知网的基础上给出了判定词义相似度的计算模型[1，5]。但是知网的构造者董振东指出知网的结构与WordNet 是有很大区别的，最大不同在于它不是一部义类词典，而是一个描述概念与概念之间关系以及概念的属性与属性之间关系的知识系统[6-7]。《同义词词林》是梅家驹等人于1983 年编撰的可计算汉语词库，经哈尔滨工业大学研究人员扩展成为《哈工大信息检索研究室同义词词林扩展版》（本文简称《词林》），其内部结构与WordNet 的分类体系较为相似，因此近年来越来越多地被应用于词义相似度计算中。

田久乐等利用《词林》的编码及结构特点，结合词语的相似性和相关性，实现了一种基于路径和深度的词语相似度计算方法，对于两个词语义项s1和s2，其相似度计算公式如下：

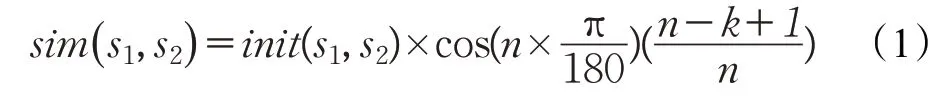
其中，init(s1,s2)是相似度初值函数是相似度初值调节参数，n是分支层结点总数，k是两个义项在最近公共父结点中的分支距离[8-9]。

朱新华等根据词语的分布情况，为《词林》提出的词语相似度计算公式如下：

其中，分支结点数n和分支间隔数k为调节参数，dis(C1,C2)是词语编码C1和C2在树状结构中的距离函数。该文为知网也提出了改进的义原相似度计算，最后综合考虑知网与《词林》的动态加权策略来计算最终的词语语义相似度[10]。

陈宏朝等提出了一种基于路径与深度的《词林》词语语义相似度计算方法。该方法通过两个词语义项之间的最短路径及其最近公共父结点在层次树中的深度计算两个词语义项的相似度。并提出在语义词典中任意两个义项s1和s2的相似度计算公式如下：Depth(LCP(s1,s2))表示两个义项s1和s2最近公共父结点的深度距离，Path(s1,s2)表示两个义项之间的最短路径；α为深度调节参数，β为路径调节参数[9]。

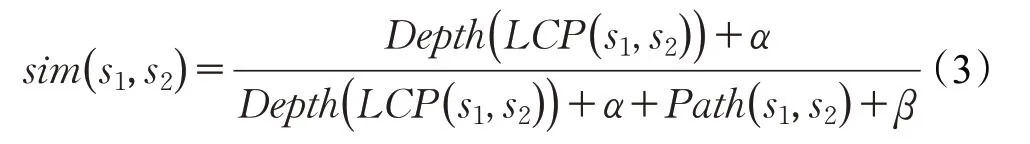
王松松等提出了一种基于路径与《词林》编码相结合的词语语义相似度计算方法，该方法使用局部敏感哈希算法将两个词语在《词林》中的编码转换成两个二进制，再使用海明距离来计算两个二进制之间的距离，具体计算公式如下：

其中，Norm表示对海明距离计算结果进行归一化处理，PathHamming(w1,w2)表示词语w1和w2之间的海明距离[11]。

综上，研究者设计《词林》词义相似度计算模型时具有以下两个特点：（1）进一步挖掘知识体系中的相关信息，并将这些信息作为计算词义相似度的关键因素；（2）进一步完善词义相似度的计算模型，建立词义相似度与关键因素之间更为合理的关系表达式。从而使得相似度计算结果更接近人工判定值，但相关算法和模型仍有需要完善的地方。

2 《同义词词林》组织架构分析

经哈工大扩展后的《词林》目前共收录词语77 456条，分为 12 个大类，95 个中类，1 428 个小类，小类下方进一步划分为4 026 个词群和17 817 个原子词群两级。每个原子词群对应一个义项编码，也对应着一组同义词条目，其中只有一个义项的词语有68 645 个，两个或两个以上义项的词语有8 811个。

《词林》体系中将词语分为五个层级，第一层级是大类，用1 位大写英文字母表示；第二层级是中类，用1 位小写英文字母表示；第三层级是小类，用2 位十进制整数表示；第四层级是词群，用1位大写英文字母表示；第五层级是原子词群，用2位十进制整数表示。在这个五层级分类体系中用7 位编码确定后就可以唯一表示一组原子词群。第8位编码有三种情况：“＝”表示原子词群中的词语属于同义词语；“＃”表示原子词群中的词语属于相关词语；“＠”表示原子词群中只有一个词语，这个词语在《词林》中既没有同义词语，也没有相关词语。表1详细展示了《词林》中的五层、8位义项编码情况（参见《哈工大同义词词林扩展版》网站：http://www.ltpcloud.com/download）。

表1 《词林》义项编码表

在《词林》的编码体系中，前面四层结点都代表抽象的类别，只有第五层的叶子结点才是具体的词语，同一个词语可能有多个不同的义项，即同一词语可能在不同的原子词群中同时存在。其中第一层级的大类代码含义如表2所示。

表2 《词林》大类代码含义表

表2 中A、B、C 类多为名词，D 类多为数词和量词，E 类多为形容词，F、G、H、I、J 类多为动词，K 类多为虚词，L 类是难以被分到上述类别中的一些词语[12]。大类和中类的排序遵照从具体到抽象的原则，如E 大类下面又分为五个中类，从“外形”到“境况”，如表3所示。

表3 《词林》E大类分支义项代码含义表

下面将《词林》体系做形式化表示：

（1）为将不同大类的层级体系整合在一起，本文在《词林》体系第一层级“大类”上面再增加一个根结点R，这样《词林》体系中的词语根据其编码就构成一个完整的六层结点、五层边的树形结构图。

（2）在《词林》体系中，所有词语都在第五层的叶子结点上，将词语集合记为S={s1,s2,…,sn},对于任意两个叶子结点上的词语(s1,s2)，其词义相似度值表示为S(s1,s2)。

根据以上形式化表示方式，可以把《词林》的义项编码转化为如图1的树形结构图。

（4）在图1的树形结构中，深度是指某个结点（叶子结点或父结点）到根结点的距离，用D表示；路径是指两个叶子结点分别到其最近父结点的边的总和，用P表示。例如图1 中，s1和s4的最近父结点是F31，那么s1到s4的路径就是s1到F31的边总数与s4到F31的边总数之和。s1到F31的边总数为2，s4到F31的边总数为2，那么s1到s4的路径P=4。结点F31的深度是其到根结点R的边的总数，因此F31的深度D=3。

图1 《词林》树形结构图

通过上文对《词林》的整体架构的分析，可以得出以下结论：

（1）知识本体对于词义相似度计算起决定性作用。基于义项编码的《词林》树形图中，不同叶子结点间的路径信息里面隐含着《词林》中的词义相似度信息，这些信息实际是作者在编著《同义词词林》时就已融入其中的世界知识。在计算词义相似度时如果能精确解析蕴含其中的丰富信息，并将其形式化后转化为计算机可执行算法，就可以计算出基于《词林》的两个词语之间的词义相似度数值。不同知识本体中蕴含着不同的分类体系和世界知识，实际上是其构建者对于世界知识和词语体系认识的不同。如果用不同的知识本体做基础去计算词语之间的词义相似度，即使使用相同的算法也会得出不同的结论。因此知识本体首先是影响词义相似度计算结果的决定性因素。

（2）父结点深度与路径具有等价关系。在引入了根结点R的情况下，《词林》有六层结点，五层边，所有的词语都位于层级体系最下面的叶子结点上，因此它们与根结点R的距离（即叶子结点深度）都相同，数值为5。而对于父结点深度只有4种取值情况，D=1，2，3，4。显然一个叶子结点的深度应该是它到其任何父结点的距离与该父结点深度之和。对于任意两个叶子结点，它们到最近父结点的距离相等，因此两个词语间的路径是它们到最近父结点距离的2倍。例如，s1和s4的父结点是F31，s1到s4的路径P=4 ，F31的深度D为3，s1和s4到F31的边数均为，因此父结点深度和路径有如下关系：

该结论说明路径和父结点深度是两个能够相互表示的量，因此在计算相似度时两者能够互相替代，从而简化算法。

（3）在同一个知识本体中，最近父结点F的深度对于两个词语的词义相似度起决定性作用。从《词林》体系中可以直观地看出来，F在《词林》体系中所处层级位置越高，D的取值越小，则s1与s2的相似度越低；相反F在《词林》中所处层级位置越低，D的取值越大，其在《词林》中所处层级位置越低，则s1和s2的相似度越高。因此D的取值与S成正比关系，而F的位置与S成反比关系。这从语言学角度也很容易理解，当两个词语所处的分支层的父结点越低，说明这两个词语所在的类别距离越近，两个词语的语义相似程度就越高，相反当两个词语所处的分支层的父结点越高，说明这两个词语所在的类别距离越远，两个词语的语义相似程度就越低。词义相似度计算问题就是将已有知识体系中的信息进行量化表达的过程，因此对知识体系中信息提取得越充分，使用得越合理，就能得到更好的计算结果。为此本文对《词林》中与词义相似度相关的信息进行了详细的统计和分析。

①分析叶子结点中词语的分布情况。在《词林》中每个叶子结点对应一个义项编码，且唯一代表一个原子词群，根据义项编码末位（即第8 位编码）判断，原子词群中的词语有三类关系：同义、相关或独立。“独立”的意思是该原子词群内部仅包含一个词语，最大的原子词群包含572个词，是县名的集合。原子词群中不同词语数量分布情况如图2所示。

对照组患者围手术期低血糖发生率为15.00%，观察组为3.33%，两组对比差异有统计学意义（P<0.05）；对照组患者围手术期伤口感染率为18.33%，观察组为5.00%，两组对比差异有统计学意义（P<0.05）。见表1。

图2 不同词语数量原子词群分布图

从图2 中可以看出，原子词群的分布符合幂率分布。包含词语个数越少的原子词群在《词林》中所占的比例越高。例如仅包含一个词语的原子词群数量最多有4 377 个，占比25.6%；包含两个词语的原子词群有4 161个，占比23.3%；而包含30个词语的原子词群只有15个。

在《词林》的构建过程中，将同一原子词群中词语的相似度定义为1，或者说原子词群是《词林》中词义相似度计算的最小单元。因此基于《词林》的词义相似度计算实际上是原子词群之间的相似度计算。仅使用《词林》的知识无法进一步比较原子词群内部词语间的相似度，特别是相关性词语的相似度无法进行进一步判断，需要借助更多知识。

②分析不同深度上结点的数量及其分支的分布情况。

从图3中可以看出，第一层中各结点包含的分支数存在较大差异，其中包含分支数最多的是结点B 类（物类），共有4 568个分支（具体分支情况见图4）；包含分数支最少的结点是L类（敬语类），仅有28个分支。

图3 《词林》第一层级各结点分支数量图

图4 B大类各结点分支数量分布图

进一步分析第一层结点的分支情况，其中A结点包含从a到n共14个不同分支，分支中包含结点最多的有291 个，最少的有19 个（具体分支情况见图5）。结点A的子结点Ae包含18个分支（详见图6）。对这些结点中的每一个结点还可以继续分析其分支数量，直到得到每一个结点所包含的原子词群中词语的数量。

图5 A大类各结点分支数量分布图

图6 结点Ae分支数量分布图

3 基于父结点深度和父结点深度与其分支信息相结合的词义相似度计算模型

在基于知识本体的词语相似度算法中，使用路径和深度计算词语相似度是非常重要的一类方法。如前所述在基于WordNet的英语词语相似度计算方法中，研究者提出了各种简单或复杂的基于路径和深度的计算方法，这些方法又可进一步划分为仅基于路径的方法、基于路径和深度的方法以及包含信息内容的方法等[4]。因为《词林》也具有清晰的词语路径和深度信息，所以这些基于路径和深度的方法都可以直接用于基于《词林》的词义相似度计算中。但由于WordNet 与《词林》的组织架构不同，在WordNet 中不同的词可能具有不同深度，这种叶子结点深度不均匀，义项遍布所有结点的组织方式与《词林》是截然不同的。

《词林》中所有词语都在叶子结点上，因此都具有相同深度，如果直接使用基于WordNet 的计算公式，就会出现得到的相似度只能取到几个有限值的情况，无法体现不同词对之间的差异。但在《词林》体系中这种取值也具有一定的合理性，在《词林》体系中，词语按照类别逐级细分，例如“人类”的语义代码为Aa01A02=，“兄弟”的语义代码为Aa02A07=“，森林”的语义代码为Bh01A03=。“人类”与“兄弟”的语义类别在同一个大类A 中，而“人类”与“森林”的语义类别不同，分别在A 大类和B 大类中，因此前两者的词义相似度一定高于后两者。如果用图1的树形结构来描述，“人类”与“兄弟”的最近父结点为处于第三层的a，其深度为2。“人类”与“森林”的父结点为R，其深度为0。所以最近父结点深度不同的两个词对所对应的词义相似度必然不同。

前期文献中的普遍结论是假设两个词语义项s1和s2的相似度S与它们最近父结点的深度D存在确定的函数关系，根据本文描述《词林》结构的树形结构图，S与D成正比关系，即D越大时S的取值越大，反之越小，且S的取值应介于[0，1]之间，为此本文给出如下简洁公式：

其中，λ1、λ2、λ3、λ4为调节参数。该式仅通过父结点深度D来计算两个词语的词义相似度S的大小，且能很好地体现D与S的关系。

公式（3）使用了距离、路径以及动态参数，当动态参数β取常数时，本文所提出的公式（6）实际与公式（3）是等价的。因为在公式（3）中Depth和Path分别是加权后的深度和路径，且每层只有一个权值，若将公式（5）代入公式（3）所得结果实质上与公式（6）结果等价。因为在《词林》中路径的深度层次有限，所以词对间相对位置的情况是有限的，因此使用公式（6）只能得到几种有限词义相似度取值。也就是说公式（6）对应函数的定义域为{0，1，2，3，4}，因此函数的值也是有限的，根据函数值与D成正比的关系，该函数是一个阶梯函数。根据上面的分析，在《词林》体系中不同阶梯会对应不同层级的词语，从语言学角度来看这样的结果具有一定的合理性。为使得词语语义相似性得到更好的描述，可以通过调整函数表达式或者加入更多语言学信息来进一步计算出更合理的词义相似度结果。公式（3）通过使用随词对变化而变化的动态调节参数β来实现相似度值的变化，其目的是为了克服只有几个有限值的不足，但是用这种做法所调节的幅度及目标值却都是不可控的，而且从语言学角度的可解释性不强。上述深度是表示两个义项分类差异的结果，在调整基于父结点深度相似度阶梯取值时，最好不要改变其相似度阶梯，因此应在阶梯取值基础上进行微调。根据这一思想，本文使用任意两个义项s1和s2最近父结点的分支信息构建微调项，对公式（6）进行微调后给出如下微调结果：

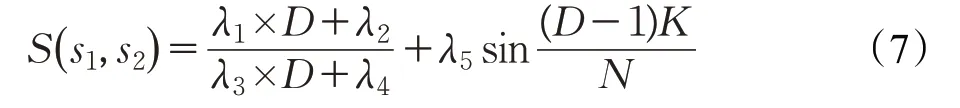
其中，D为最近父结点深度，N为其最近父结点所包含的分支总数，K为两个义项所在分支的间距。根据公式（6）中函数取值的特点及其对最大值和最小值拟合不足的问题，通过设置调整参数(D-1)来改进端点处的拟合情况，为避免微调项改变和否定父结点深度确定的相似度层级问题，引入正弦函数进行调节。

4 实验与分析

Rubenstein 等让51 名被试对65 个词对（简称为RG65）进行“同义判断”，这65个词对的语义从“高度相似”到“语义无关”不等，被试需要根据对这些词对的语义相似性判断，在0.0～4.0 范围内给词对打分[13]。后来Miller 等从 RG65 中提取了30 个词对（简称为MC30），这30对样本中有10对词语的语义具有高相似性，有10对词语的语义具有中相似性，还有10 对词语的语义具有低相似性，然后从被试样本中抽取38 份样本作为MC30的人工语义相似性判断结果[14]。本文也以此作为判断标准。

本文将在《词林》的基础上，参考MC30人工判别结果，使用鱼群算法建立描述词义相似度的关系模型，以期突破根据先验经验建立函数模型的局限性。人工鱼群算法是李晓磊等人于2002年提出的一类基于动物行为的群体智能优化算法。该算法是通过模拟鱼类的觅食、聚群追尾、随机等行为在搜索域中进行寻优，是群体智能思想的一个具体应用[15]。由此本文对公式（6）和（7）中的系数分别表示为4维和5维向量Λ1,Λ2，这样可以把待优化的参数看作人工鱼个体，通过构建鱼群分别寻找最优参数。首先使用鱼群算法对公式（6）中的系数进行寻优，最后得到的系数分别为：λ1=0.981 1,λ2=0.497 7,λ3=0.124 4,λ4=4.461 2 。

再使用鱼群算法对公式（7）中的系数进行寻优，最后得到的系数分别为：

λ1=0.836 6,λ2=0.443 1,λ3=0.167 7

λ4=3.779 3,λ5=0.098 7

将第一组系数代入公式（6）得到基于父结点深度的词义相似度计算方法，将第二组系数代入公式（7）得到基于父结点深度与其分支信息相结合的词义相似度计算方法。使用这两个方法分别对MC30 进行词义相似度计算，计算结果如表4所示。

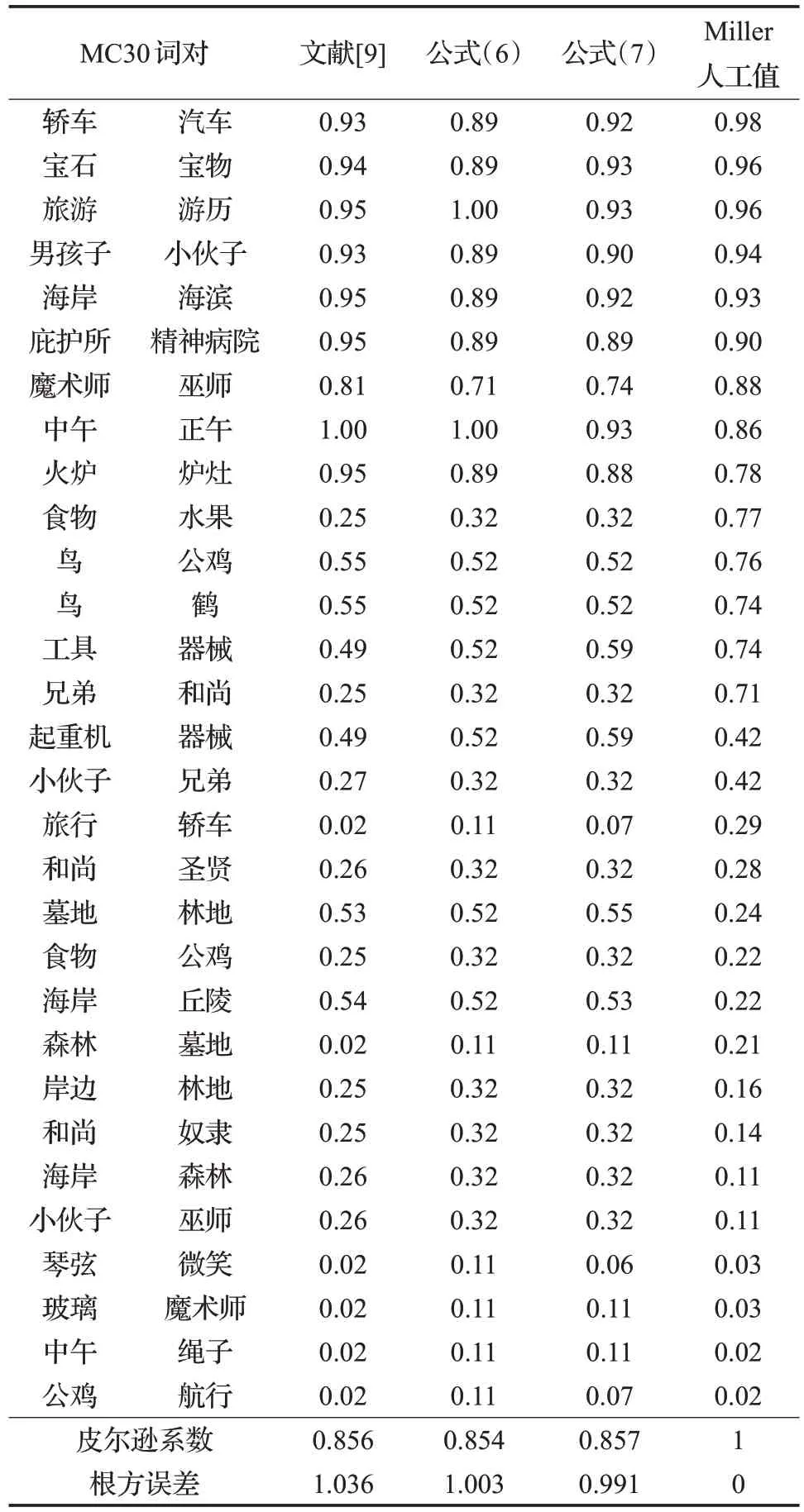
表4 MC30词对实验结果对比表

表4 中分别列出了公式（6）和公式（7）的相似度计算结果，以及文献[9]的结果，从中可以看出，公式（6）虽然仅使用父结点深度信息，但仍能得到较好的计算结果，其结果与人工值间的皮尔逊系数为0.854，与文献[9]的结果0.856 仅有微小差异，均优于该文献中列出的其他方法，这说明在《词林》的框架体系中，父结点深度对相似度起到决定性作用。此外还计算了根方误差，该值是使用不同算法计算MC30 词义相似度结果与人工值之差的平方和再开根号，显然该值较文献[9]相应结果更小。公式（7）不仅使用了父结点深度信息，还将两个词最近父结点的分支信息结合了进来，因此计算结果得到了进一步提升。具有最高的皮尔逊系数和最小的根方误差。

显然在各种方法的计算结果中均存在与人工值差别较大的义项，例如“食物”和“水果”这一组词对，其人工判定值较高而《词林》中计算的值都很低。在《词林》中两个词语的编码分别为Br03A01=和Bh07A01=，并且被分在“物品”和“植物”两个不同的中类里面，因此其相似度较低。这种差异实际上是《词林》和人工判别方法所使用的知识体系之间存在的差异，而本文算法能较好地刻画《词林》体系中所蕴含的词义相似度信息。

此外造成这种结果的原因还可能来自于不同语言间的差异，因为人工判定值是基于英语词汇进行的，而上述算法都是翻译为对应的汉语词汇后基于《词林》进行的。这种现象从索绪尔结构主义语言学的基本观点来看就很容易理解，语言是由能指和所指构成：能指是指语言的音响和形象，即语言的读音和书写形式；所指是指语言的概念和内容。语言是一个符号系统，具有任意性，这种任意性的关系又叫约定性，即符号的形式和意义的结合是由社会“约定俗成”的，而不是它们之间有什么必然、本质的联系。因此不同符号体系、不同语言系统中的所指对应的能指可能不尽相同，而不同语言体系中能指所要表示的所指可能也会存在一定差异。因此不同语言体系的人在表达同一个所指时，因为能指的不同可能就会存在一定的理解差异，这样就造成了在不同语言体系中，所指相同的情况下，能指之间的词义相似度判断也会存在一定的差异。

5 结语

（1）本文指出在《词林》中父结点深度和路径是一对等价概念，基于父结点深度的词语的词义相似度计算方法利用简单的计算公式就能得到较为理想的计算结果。算法简洁便于其在相关工作中的使用，如短语结构相似度或句子相似度的计算。算法简洁使得算法更能体现词义相似度计算所需的核心知识，在《词林》体系中父结点深度是词义相似度的决定性因素，而不是分支信息，分支信息对词义相似度的计算只能起到微调作用。给分支信息赋予过高的权重从语言学角度来看也很难解释。此外，使用核心知识可以避免过拟合现象的发生，使得算法具有更好的泛化能力和适应性。

（2）在实验过程中发现有些词语的相似度与人工标注值存在较大差异，除进一步改善计算方法外，英汉两种语言在语言符号的音义表达系统中存在差异这一现象是客观存在的，因此英语词语之间的词义相似度与其在汉语中对应的词语之间的词义相似度可能总会存在一定的差异。因此本文在相关系数达到实用性要求的条件下，主要关注提高算法易用性和分析算法所体现的语言学原理。

（3）不同知识本体建立者因为对世界知识理解的不同，其构建的知识本体也会存在较大差异，因此《词林》和WordNet对词语相似度的体现也必然存在差异，这对基于两个知识本体分别判断词语之间的词义相似度会有较大影响。

（4）由于《词林》框架设计原因，目前基于《词林》的词义相似度算法都是针对不同原子词群间的词语进行的，相同原子词群内部词语间的相似度或相关度判别需要进一步借助其他知识本体，如知网中的信息才能进行，这是下一步需要研究和关注的内容。