结构化支持向量机研究综述

王 霞，董永权，于 巧，耿 娜

1.江苏师范大学 计算机科学与技术学院，江苏 徐州 221116

2.江苏师范大学 电气工程及自动化学院，江苏 徐州 221116

1 引言

作为一种强有力的分类和回归方法，支持向量机（Support Vector Machine，SVM）已经取得非常显著的研究成果，并广泛应用于许多领域[1-7]。支持向量机基于统计学的结构风险最小化原则[8]，通过软间隔最大化获得正类和负类间最优划分超平面。对于非线性情形，可以使用核技巧[9-11]，将低维空间的数据映射到高维空间，使用二次规划（Quadratic Programming，QP[12]）技术完美解决原始问题的对偶问题，从而获得划分超平面。

然而，传统支持向量机存在两个显著弱点，严重制约其发展。其一，在处理复杂结构数据时，计算复杂度高、实现难度大。其二，划分超平面不偏不倚，处于两个类的平行超平面的正中间，丢失了数据内在的几何结构信息。针对上述弱点，许多学者提出诸多改进方法。这些方法也相应地分为两类：一类是建立更为高效算法，诸如分解算法[13]、分块算法[14]、序列最小化优化算法[15]等；另一类则将单个最优超平面延伸为多个超平面（即非平行超平面），如此一来，各类数据点就能靠近各自的超平面，而远离其他超平面，例如广义支持向量机（Generalized Eigenvalue Proximal Support Vector Machine，GEPSVM[14]）、孪生支持向量机（Twin Support Vector Machine，TWSVM[16）]、双边界支持向量机（Twin Bounded Support Vector Machines，TBSVM[17]）、非平行支持向量机（Nonparallel Support Vector Machine，NPSVM[18]）等。

上述对SVM 的改进方法，尽管从一定程度上改善了SVM 的性能；但是，这些方法都局限于分解数据本身，忽略了数据内在的结构紧密性。不仅导致算法的复杂度较高，而且非常容易产生噪声数据处理上的失误，严重影响分类的准确性。

鉴于此，学者们提出结构化支持向量机（Structural Support Vector Machine，SSVM）。SSVM的分类过程分为两步：首先采用无监督学习的聚类方法，诸如KNN[19]、最邻近聚类[20]、模糊聚类[21-22]、系统聚类[23]等，提取数据样本内在的结构化信息；然后，以协方差矩阵的形式，将结构化信息嵌入到原始问题的目标函数或约束条件中，再对原始问题进行常规化训练。典型代表有：结构化最大边界机（Structured Large Margin Machine，SLMM[24]）、最小最大概率机（Minimax Probability Machine，MPM[25）]、最大最小边界机（Maximin Margin Machine，M4[26]）、结构正则化支持向量机（Structural Regularized Support Vector Machine，SRSVM[27-28]）、结构化孪生支持向量机（Structural Twin Support Vector Machine，STWSVM[29-30）]、结构化非平行支持向量机（Structural Nonparallel Support Vector Machine，SNPSVM[31-32]）等。

目前，针对SSVM 的理论研究成果已经非常丰硕，并成功用于解决图像识别、文字处理、控制管理等实际问题。可见，对SSVM进行系统性的阐述和评价是非常必要的；需要说明的是，尽管对非结构化SVM 的综述研究较多，例如安悦瑄[33]、Ding S[34-35]、Huang H 等[36]对TWSVM的综述，Ding S等[37]对NPSVM的综述；然而迄今为止，对于SSVM的综述研究，仍非常少见。为此，本文分析各种SSVM模型，并对部分代表性成果进行对比分析，从而揭示各种方法的优缺点、改进分析，从而为后续研究指明方向。

2 相关理论基础

2.1 结构粒度

定义1[23]对于给定的数据集，设S1,S2,…,St是根据某关系测度对数据集T的划分，且S1⋃S2⋃…⋃St=T，那么，则称该划分是以聚类结构表示的数据集，Si(i=1,2,…,t)为结构粒度。

依据实际问题对数据的处理需求，结构粒度可以分为四类：全局粒度，类粒度，聚类粒度和点粒度，如图1所示。图1中，“○”和“△”分别表示两类。

图1 结构粒度示意图

2.2 结构化支持向量机

其中，Σ=ΣP1+ΣP2+…+ΣPCP+ΣN1+ΣN2+…+ΣNCN，用分别表示正类样本和负类样本的聚类协方差矩阵；c ＞0 为惩罚参数，一般由应用问题决定。c值大（小）时，对误分类的惩罚增大（减小）；ξi≥0为松弛变量，主要用于解决某些样本点不能满足硬间隔要求；λ≥0 为聚类内结构信息权重的正则项。

3 结构化支持向量机的研究进展

SVM 的优点明显，包括具有稀疏性、能用同一目标函数处理线性和非线性问题等；但是，SVM 只关注数据类别本身，没有挖掘数据内在紧密性信息。结构粒度恰好能够反映实际分类算法中需要考虑的数据内在结构信息，因此，结合类间的离散性和类内的紧密性，从纵向（结构粒度）和横向（典型的支持向量机训练算法）讨论结构化支持向量机的现有研究成果，是十分必要的。接下来，纵横结合，探讨SSVM 的发展历程和优缺点。

3.1 结构化支持向量机

3.1.1 全局粒度支持向量机

2007 年，Shivaswamy 等首次提出椭球形核机器（Ellipsoidal Kernel Machines，EKM[38]）模型。EKM 从全局粒度出发，基于结构风险最小化原则，采用椭球有界容错分类器来提高泛化能力。EKM不需要额外的领域知识、规范，在VC 维上寻找更紧密的边界，以改进SVM 的线性决策边界；但仅仅按照全局粒度提取结构化信息、粒度过粗、性能差。

3.1.2 类粒度支持向量机

Lanckriet 等人用已知的均值和协方差矩阵，表示类内数据间的结构化信息，并提出最大最小概率机（MPM[25]）。MPM能够最小化最坏情况下未分类数据错分的概率，为分类的准确率提供一个下边界，同时通过控制错分率达到分类最大化的目的。

针对SVM 只考虑局部数据和MPM 仅考虑全局数据的不足，Huang等人提出了最大最小边界机（M4[26]），综合分析局部和全局数据，构建SVM 和MPM 的统一框架，结合二者的优点解释和扩展线性判别分析。

鉴于MPM 和M4都无法处理不平衡数据的问题，Huang 等提出偏置最小最大概率机（Biased MPM，BMPM[39-40]），和最小错误最小最大概率机（Minimum Error MPM，MEMPM[41-42]）。与 MPM 相比，MEMPM 取消了对两个类最坏精度的等式约束，在最坏情况下最小化测试数据的贝叶斯分类错误率，从而实现了最坏情况下的最优分类器。

针对既有模型不能预先对数据作出有效预测，Yoshiyama 等提出流形正则最小最大概率机（Manifold-Regularized MPM，MRMPM[43]）。MRMPM 在目标函数中增加流形正则项，以提取数据样本内在的几何信息，从而提高分类的准确性。

结合半监督学习技术，Yoshiyama 等提出了拉普拉斯最大最小概率机（Laplacian MPM，Lap-MPM[44]）。Lap-MPM以图正则[45]平方根的形式，显式地修正MPM的异常。

MPM、BMPM和MEMPM在训练数据时，对非标记样本关注不够。为此，王晓初等提出基于数据分布一致性最小最大概率机（MPM with Concensus Regularization between Data Distributions，DCMPM[46]）。通过最小化有标签样本和无标签样本在决策超平面所在空间概率分布差距，充分利用无标签样本来修正最小最大概率机的误差。

为修正MPM 和MEMPM 中存在的过拟合现象，提高泛化性能，Maldonado 等人提出正则化最小最大概率分类器（Regularized MPM，RMPM[47]）。在求解时，将权重向量的L2范数与错误率合并最小化，采用非线性SOCP技术获取划分超平面。

表1列出上述几种模型优缺点的对比。

3.1.3 聚类粒度支持向量机

这是研究结构化支持向量机比较成功的一类，其代表是SLMM和SSVM。

表1 类粒度支持向量机优缺点对比

2007年，Yeung等提出结构化最大边界机（SLMM[24，48）]。SLMM将数据结构量化分为两步：（1）通过Ward凝聚法对数据点进行聚类；（2）计算各聚类的协方差矩阵，进一步进行距离测量。尽管SLMM 的分类效果较好，但是，计算复杂度高，通常需要使用SOCP 求解最优化问题，实现难度大。

针对上述问题，Xue等提出结构化支持向量（SSVM[27）]。将结构化信息与标准支持向量机训练过程结合，以协方差矩阵的形式将结构化信息添加到标准支持向量机的目标函数中，然后再按照SVM方法求解目标函数，获得分类超平面。SSVM 将数据样本类内的紧密性和类间的离散性结合考虑，所以无论从泛化处理能力还是实际运行效率，都高于标准SVM；同时，从本质上解决了SLMM的计算复杂度高的问题。后续的有关结构化支持向量机的研究，基本上都是SSVM模型为基础发展和完善的。

尽管SSVM 优势明显，但是，存在过拟合现象。为此，Xue 等提出结构化正则支持向量机（SRSVM[28]）。SRSVM 首次提出“结构粒度”的概念，同时利用聚类技术提取样本数据内在的结构信息，并应用于SVM 的学习过程，使用QP技术和对偶原则求解。SRSVM不仅降低了计算的复杂度，而且提高了分类的准确率。

表2列出上述几种模型优缺点的对比。

3.1.4 点粒度支持向量机

2006 年，Belkin M 等提出拉普拉斯支持向量机（Laplacian SVM，LapSVM[49]）。LapSVM是一种基于流形正则项的半监督分类算法，主要研究利用少量的有标识的样本和大量的未标识样本进行训练和分类。

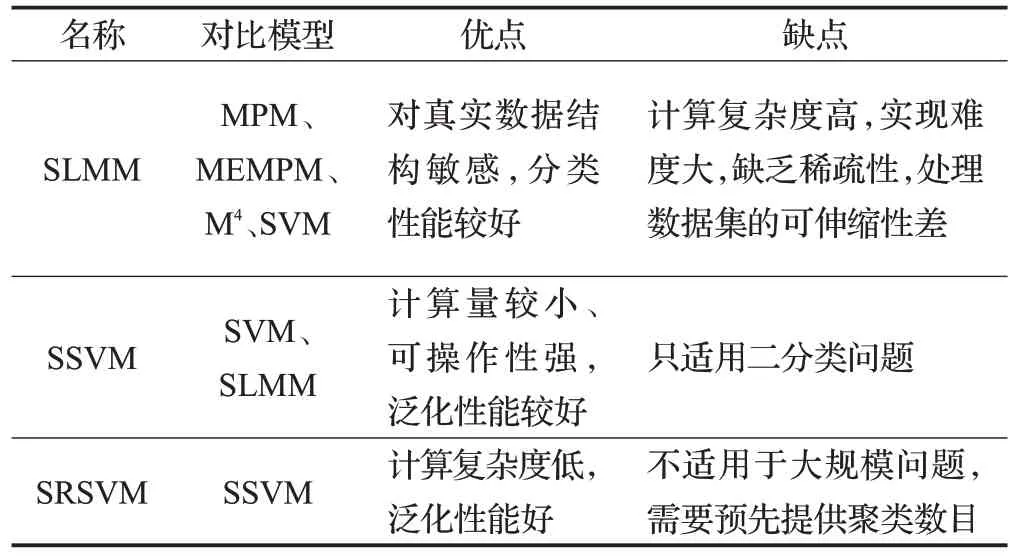
表2 聚类粒度支持向量机优缺点

从理论上讲，LapSVM中引入了包含样本的固有几何结构信息的样本流形正则项，分类结果更准确。但在实际问题解决过程中，LapSVM算法涉及许多矩阵运算和转换，时空复杂度较高。近年来，为提高LapSVM 算法的运行速度和分类准确性，学者们提出许多新的算法。

Lee S 等提出改进的LapSVM（Structural Laplacian SVM，SLapSVM[50]）。这是一种基于方差分解原则的SLapSVM，通过对分量引入额外的惩罚因子，产生稀疏矩阵，从而有效提高半监督学习结果分类器的可解释性。

为了进一步提高LapSVM 性能，Melacci S 等提出加速拉普拉斯支持向量机（Laplacian SVM Trained in the Primal，PLapSVM[51]），该方法包含两种加快计算性能的算法：PLapSVM-Newton和PLapSVM-PCG，分别采用牛顿迭代法和预处理共轭条件法（Preconditioned Conjugate Gradient，PCG[52]）获取最优解，计算复杂度降低。

针对PLapSVM在无法直接处理大规模数据问题的不足，Qi等提出快速拉普拉斯支持向量机（Fast Laplacian SVM，FLapSVM[53]）。FLapSVM 无需处理矩阵或与变量相关的计算，因此，更适用于大规模问题的求解，且计算性能比LapSVM 更好；使用相同的对偶问题处理线性和非线性问题，泛化性能好；同时采用逐次超松弛（Successive Overrelaxation，SOR[54）]技术获取问题最优解。

LapSVM在求解优化问题时，只考虑问题本身性质，而忽略问题规模，从而失去稀疏性。为此，Yang等提出一种有效的基于LapSVM安全筛选规则（Safe Screening Rule for LapSVM，SSR-LapSVM[55]）。SSR-LapSVM 是一种不丢失最优解的快速LapSVM 算法。通过对KKT条件和对偶问题可行集的分析构造，得出解析规则。利用解析规则进行筛选，在求解QP问题之前，获取最优解的某些分量，大大减少训练样本的数量，从而提高优化效率和速度。

表3列出上述几种模型优缺点的对比。

表3 点粒度支持向量机优缺点总结

3.2 结构化孪生支持向量机

研究发现，全局粒度、类别粒度过于粗糙，不利于提高分类的性能；点粒度过于精细，显著增加计算的复杂度，因此，近年来对结构粒度的研究，多集中于聚类粒度的层次。

结构化孪生支持向量机（STWSVM[30）]是在TWSVM基础上，加入结构化信息发展而来的。STWSVM 结合结构粒度和标准支持向量机的思想，在构造TWSVM时，先利用聚类技术挖掘类内结构信息，再将数据分布信息引入TWSVM模型，从而构造出更合理的分类器。

鉴于TWSVM 的非平行超平面不能刻画数据的分布特征，而且计算复杂度高的不足，Peng等提出结构双参数边缘支持向量机[29（]Structural with Parametric-Margin SVM，STPMSVM）。STPMSVM 在标准双参数边缘支持向量机（Twin Parametric-Margin SVM，TPMSVM[56）]基础上，用马氏距离取代欧氏距离，分别考虑两类数据中聚类的协方差矩阵。这种策略可以充分利用不同类型数据中的信息，从而达到更好的泛化性能。

针对传统TWSVM只关注类间数据离散性的弊端，Wang Z 等提出孪生支持向量机聚类（TSVM for Clustering，TWSVC[57]）。通过求解一系列二次规划问题，确定了k个聚类中心平面。并且提出了一种高效、稳定的基于神经网络的初始化方法。

针对STWSVM 计算复杂度高的不足，Pan X 等提出基于KNN 的孪生支持向量机（K-Nearest Neighbor based STWSVM，KNN-STSVM[58]）。先使用 KNN 聚类技术提取样本数据内在结构信息，并且根据样本密度给予不同聚类相应的权重，同时分别使用两个最邻近图Ws和Wd（类内和类间）来计算样本权重来提取相应的结构信息；再使用类似TSVM 的方式来训练数据，从而获取两个划分超平面。KNN-STSVM 具有分类准确率高、计算复杂度低等优点。

使用凝聚层次聚类方法的结构化支持向量机（如SRSVM、STSVM 和KNN-STSVM）在提取结构化几何信息时，只考虑类内局部结构，不考虑类间局部结构。为此，Chu M 等提出局部结构信息的孪生支持向量机（TWSVM with Local Structural Information，LSITSVM[59]）。LSI-TSVM 嵌入了数据在类内和类间的局部分布信息，不仅包含了原始的类内全局聚类和类间边缘，而且包含了类内和类间的局部散点。

针对STWSVM 无法直接进行多分类处理的问题，Hanifelou Z等提出基于KNN的多标签优先级的TWSVM（KNN-based Multi-Label Twin Support Vector Machine with Priority of Labels，PKNN-MLTSVM[60]）。首先使用K邻近图获取数据的局部几何信息，再利用聚类技术提取样本的内在结构信息，最后结合结构信息和几何信息获取划分超平面。

KNN-STSVM存在过拟合的缺点，为此，Xie F等提出正则KNN结构化孪生支持向量机（Regularized KNNSTSVM，RKNN-STSVM[61]）。通过在目标函数中增加正则项来提高算法的泛化能力，从而避免过拟合，提高计算性能。

针对STWSVM 不能直接处理不平衡数据的不足，Mohammadi F S 等提出结构化加权松弛孪生支持向量机（Twin Structural Weighted Relaxed SVM，TSWRSVM[62]）。TS-WRSVM利用两个非平行超平面来训练数据，使得每个模型只考虑本类的结构信息，并且根据每个类的大小，为每个模型分配一个权重和有限的无惩罚的松弛变量。TS-WRSVM可以降低异常值和噪声对训练边界的影响，提高分类器在处理不平衡分类问题时的性能；具有较低的计算复杂度、较高分类准确度和泛化能力。

表4列出上述几种模型优缺点的对比。

3.3 结构化非平行支持向量机

鉴于TWSVM在求解目标函数时，其算法整体性能低下，同时无法直接将线性问题扩展为非线性问题。为此，Tian 提出非平行支持向量机NPSVM，NPSVM 不仅没有矩阵逆运算，而且线性问题与非线性问题的原始问题是统一的。但是，由于NPSVM仅考虑类间数据的离散性，没有考虑类内数据的紧密性，从而分类准确率低。

为此，Chen等将结构化信息同非平行支持向量机结合，提出结构化非平行支持向量机（SNPSVM[31]），以提高分类器的准确性和泛化能力。他们还将改进型交替方向乘子法（Alternating Direction Multiplier Method，ADMM[63]）引入SNPSVM，从而提高了模型的训练效率。SNPSVM 的训练过程分为三步：（1）采用聚类挖掘数据结构信息；（2）通过学习获取划分超平面；（3）采用ADMN优化算法性能。

然而，SNPSVM 无法直接处理大规模数据，针对这一问题，Chen 基于LSH 提出结构化非平行支持向量机（SNPSVM based on LSH，LSH-SNPSVM[64]）。LSHSNPSVM 在对分类器进行训练前，通过有效的哈希函数，过滤多余空间。此外，采用ADMM 对SNPSVM 进行了有效求解。

针对非并行分类器忽略了不同样本间的判别信息的不足，Hou Q等提出基于判别信息的非平行支持向量机（Discriminative Information-based NPSVM，DINPSVM[65）]。对每个超平面分别构造类间子图Gs和类内子图Gd，提取数据内在的空间几何信息，再将从Gs和Gd得到的两个相应的权矩阵Ws和Wd分别赋给类内判别正则项和类间判别正则项，并添加到目标函数中进行训练。此外，为降低计算复杂度和空间存储，在类间正则化项中只保留潜在支持向量样本，从而提高NPSVM的执行效率和有效性。

表5列出上述几种模型优缺点的对比。

表4 结构化孪生支持向量机优缺点对比

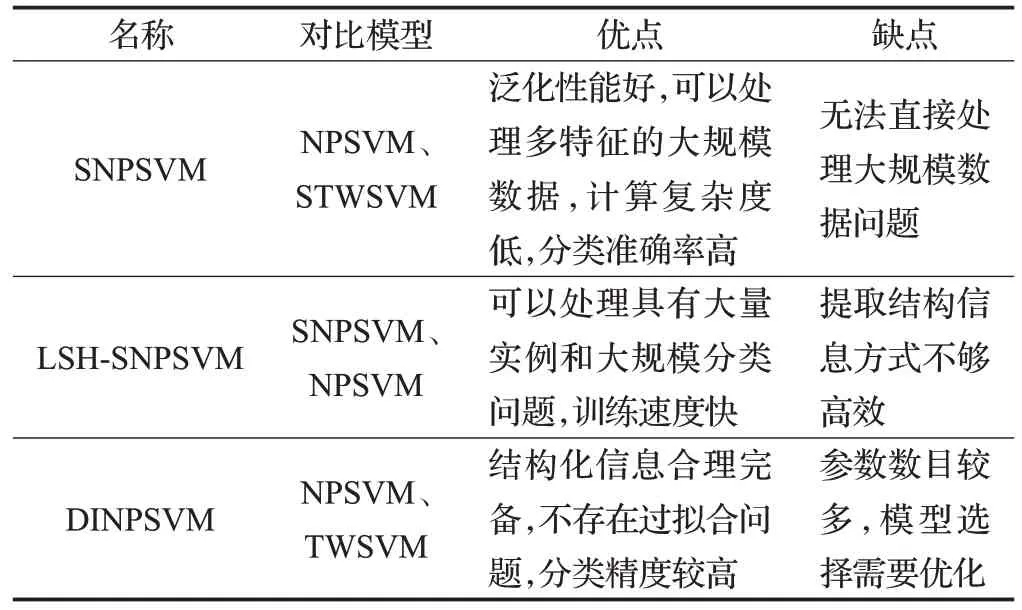
表5 结构化非平行支持向量机优缺点总结

4 各种结构化支持向量机实验比较

为了对比分析各种结构化支持向量机的性能，验证其优点，进一步寻找算法改进的方向。结合前面论述，从聚类层次结合结构化支持向量机的发展历程，选取三组比较有代表性的SVM-SRSVM、TWSVM-STWSVM、NPSVM-SNPSVM 进行对比实验；并选用自制数据（100×2）和UCI 机器学习数据库中八个常用的数据集（见表6），以测试上述算法。为了保证实验的可靠性，将80%的数据样本作为训练数据，20%的数据样本作为测试数据，对训练数据，参数c和λ从{2-10,2-9,…,29,210}范围采用十字交叉验证法选择最优值；同时使用无监督聚类学习方式，先对训练数据进行聚类，聚类数目依据肘部法则[66]自动选取；接下来用选取的最优值对测试数据进行测试，评价算法的分类准确率。实验基于Matlab R2016b进行，硬件配置为8 GB内存，Intel®Core™ i5处理器和3.30 GHz 主频。表7、表8 分别列出三组模型在八个数据集中的分类准确率和运行时间。图2～4 分别为SVM与SRSVM、TWSVM与STWSVM和NPSVM与SNPSVM 在自制数据集上运行结果对比图。图5（a）～（f）为三种模型分类准确率和运行时间对比图。

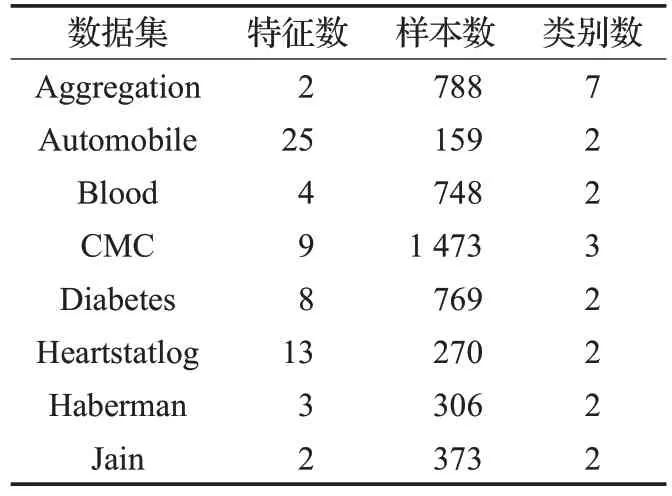
表6 UCI数据集的信息

从图2 可以看出，SRSVM 与SVM 所获取的支持向量机个数基本相等，前者分类准确率较高，运行时间短。即使在SRSVM训练数据前要对数据进行聚类提取结构化信息，并以协方差的形式嵌入到目标函数中进行训练，理论上增长运行时间，但所需时间比求解优化问题所需要的时间要短得多，所以整体运行时间较短。

表7 三组模型的分类准确率比较（运行十次的平均值）%

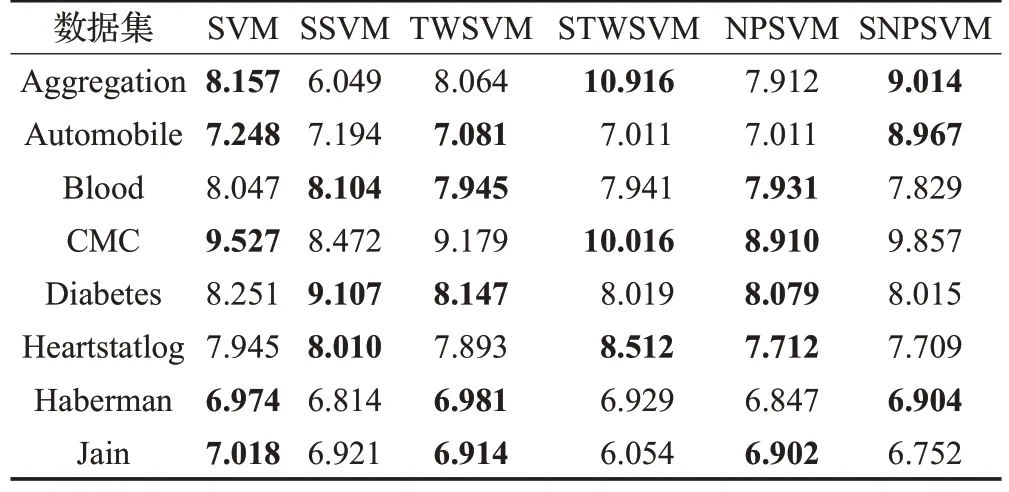
表8 三组模型的运行时间比较（运行十次的平均值）s

图2 SVM与SRSVM运行结果对比图

图3 TWSVM与STWSVM运行结果对比图

从图3可以看出，TWSVM与STWSVM都生成一对平行超平面；由于后者首先使用聚类技术提取结构化信息，消除了多余支持向量机对分类结果的影响，只保留潜在且合理的支持向量，故STWSVM 支持向量机数目减少，但是分类准确率提高。虽然在STWSVM 中也要在目标函数中嵌入表示结构化信息的协方差矩阵，但是由于TWSVM本身的优势，故运行时间也没有增加。

图4 NPSVM与SNPSVM运行结果对比图

图5 三种模型分类准确率和运行时间对比图

从图4 可以看出，NPSVM 与 SNPSVM 都生成一对非平行超平面；由于后者首先使用聚类技术提取结构化信息，不仅减少了支持向量机数目，而且分类超平面更加贴合数据集本身的几何表示，分类准确率高。

从图2～图4还可以发现，结构化比非结构化的准确率高，运行时间有高有低，且结构化非平行支持向量机的分类准率最高，这也成功验证了学者对支持向量机的研究方向和成果。

图5（a）～（c）分别为三种模型（SVM 与 SRSVM、TWSVM 和STWSVM、NPSVM 与SNPSVM）分类准确率的折线对比图，蓝色实线表示相应的结构化支持向量机的分类准确率，红色虚线表示的是非结构化支持向量机的分类准确率。（d）～（f）分别为三种模型运行时间折线图，蓝色实线表示相应的结构化支持向量机的运行时间，红色虚线表示的是非结构化支持向量机的运行时间。

非常直观，非结构化支持向量机表现相对稳定，结构化支持向量机结果存在不稳定现象，原因在于数据集的特征数和类别数目不同，特征数越多，提取的结构化信息越不完备，分类结果就不甚理想。所以说，现有的结构化支持向量机不太适合处理多特征大规模问题。

5 总结和展望

本文深入讨论了结构化支持向量机，并对近年来多种类型的支持向量机结构化研究成果进行分析和比较。结构化支持向量机是采用无监督聚类，获取样本数据内在的几何结构信息，通常以协方差或均值的形式，嵌入到支持向量原始问题的目标函数或约束条件中进行训练，从而将类内的结构性和类间的离散性结合考虑，大大提高了分类器的准确性，并增加了算法的泛化性能。近年来，人们针对结构粒度、参数选择、优化方法等多方面提出许多结构化模型；在聚类方法的选择上，大多集中于使用系统聚类、肘部法则进行聚粒度选择。在实际应用中，结构化支持向量机仍需要在以下方面进行改进：

（1）更加有效的智能算法提取结构化信息，提高模型的计算效率，从而使分类器具有更好的性能。

（2）结构化支持向量机虽然已被运用于多标签分类中，但仍存在准确度较低、计算复杂度高等缺点。

（3）结构化支持向量机应用于大数据也面临许多挑战。

（4）标准支持向量机的应用比较广泛，但是结构化支持向量机的应用不多，如何将结构化支持向量机应用解决实际问题，是今后研究的方向。