面向可加工性的矩形件优化下料算法

鲁淑飞，陈 燕，崔耀东

广西大学 计算机与电子信息学院，南宁 530004

1 引言

二维矩形件下料广泛存在于服装、皮革、木材、金属制品、机械设备等生产制造行业，作为控制企业生产成本的重点环节，采用合理的优化下料技术具有重要的意义[1]。如在钢材、机械、汽车、造船等重工业领域，由于钢板一般通过激光、火焰、等离子切割以及冲裁等方式切割成生产零件，切割成本较高，因此采用在提高材料利用率的同时，降低切割成本，缩短生产周期的优化下料技术，对于企业长远发展具有重要意义。

目前针对矩形件优化下料问题，国内外专家学者大多从改进算法提高材料利用率角度进行研究，文献[2]应用四块排样算法生成单个排样方式，与基于价值修正的顺序启发式算法相结合，选择使用板材张数最少的下料方案作为最终解；文献[3]应用生成同质条带四块排样方式的背包算法，与线性规划算法相结合，以板材张数最少为目标选择下料方案；文献[4]将列生成法与有约束排样方式算法相结合，求解同质条带四块排样的矩形件下料问题以提高材料利用率；文献[5]提出一种可以确定板材采购尺寸的二维优化下料算法，即在已知矩形件需求的情况下，在供应商规定的板材尺寸范围内确定最佳采购尺寸，使板材利用率达到最优，降低材料成本。然而矩形件优化下料问题是具有最高计算复杂性的NP完全问题，实际下料问题涉及环节多，生成下料方案时，不仅要考虑材料利用率，同时还要考虑下料工艺、切割成本、生产效率等一系列问题，使下料方案在具有高材料利用率的同时具有良好的可加工性[6]、低的切割成本和高的生产效率。针对实际下料过程中的一些具体问题，文献[7]提出一种支持一刀切工艺约束的放宽式搜索算法，在得到高材料利用率下料方案的同时满足特定下料工艺；文献[8]将基于分组降维规则与遗传算法相结合，求解人造板矩形件优化下料问题，解决一张板材上布局矩形件种类过多导致开料锯在切割过程中锯路繁琐开料速度慢的问题；文献[9]考虑下料方案的可加工性，将根据板材单方向余料长最小化优选条带方法与基于条带的连续启发式算法相结合求解矩形件优化下料问题，利用同质条带的共边排样设计自动切割工艺的下料切割路径，以缩短总的切割路径，提高生产效率，降低下料切割成本。但是其利用板材单方向余料长最小化优选布局条带的方法不能保证排样方式全局最优，另外基于布局条带的连续启发式算法具有贪婪性，即生成下料方案中靠前排样方式时，剩余矩形件多，容易得到高材料利用率的排样方式；在生成靠后排样方式时，剩余矩形件较少，得到排样方式的材料利用率较低。

基于以上研究基础，针对钢板矩形件自动化切割下料问题，本文综合考虑材料成本、下料工艺、切割成本以及生产效率，将同质条带多级规范布局方式[10-11]生成算法与基于价值修正的顺序启发式算法[12-13（]Sequential Value Correction，SVC）相结合，以材料成本和切割成本为优化目标，提出一种面向可加工性的矩形件优化下料算法。最后通过多组算例进行实验对比，证明应用本文算法能够有效地提高材料利用率和生产效率，降低切割成本。

2 数学模型及相关概念

2.1 问题描述及数学模型

本文讨论的是多规格、大批量的矩形件优化下料问题，即在n种长为Lj，宽为Wj，供应量为Dj(j=1,2,…,n)的板材上按照生产工艺要求切割出m种长为li，宽为wi，需求量为di(i=1,2,…,m)的矩形件。

假设下料方案有K种排样方式，对于第k(k=1,2,…,K)个排样方式，Sk为消耗的材料成本，λPk为切割成本（其中λ为控制参数，Pk为切割路径长度，切割成本与切割路径长度成正比，λ∈[1,12]，默认值为7），aki为含第i种矩形件的数量，xk为使用次数，所使用的板材种类为β(k)，其中β(k)∈[1,2,…,n]。要求满足矩形件需求量，并使其生产成本（材料成本与切割成本之和）达到最小。则该问题的整数规划模型为：

其中，式（1）为面向可加工性的矩形件优化下料问题的目标函数，即最小化的生产成本，其中板材成本为板材面积，切割成本为下料过程中能源、加工工时、人力资源等消耗通过控制参数以切割路径总长度为单位统一折算而来；式（2）为约束条件，表示按此下料方案产出的矩形件数量应该等于矩形件的需求；式（3）为约束条件，表示下料方案使用每种板材的总量不能超过其供应量；式（4）为变量的取值范围，Z+0表示非负整数集合。

2.2 条带

条带根据是否含有多种不同尺寸的矩形件，可分为普通条带和同质条带。如图1所示，由不同宽度的矩形件组成的条带称为普通条带，由相同种类相同方向的矩形件组成的条带称为同质条带。综合考虑下料方案的可加工性，以及自动化切割的可操作性，本文采用同质条带。

图1 条带

分别用X和Y标记水平方向和竖直方向，则根据条带方向与矩形件长边的方向，可将条带分为XX、XY、YX和YY四种类型。其中，XX型条带表示条带方向水平，矩形件长边水平；XY 型条带表示条带方向水平，矩形件长边竖直；YX型条带表示条带方向竖直，矩形件长边水平；YY 型条带表示条带方向竖直，矩形件长边竖直。四种条带在板材上的布局如图2所示，其中阴影部分为条带在板材上排样后所产生的余料。

图2 四种条带布局示意图

表1分别列出了各类型条带的相关标记参数，则各类型条带的相应价值如下：

表1 条带相关参数信息表

其中，ci为第i种矩形件的价值，i=1,2,…,m。

2.3 板材切割

板材切割即按排样方式切割出板材上所布局的矩形件。本文板材切割方法参考文献[9]，条带内的矩形件分离采用“之”字型切割，条带间的分离采用直线型切割。条带内的矩形件分离具体切割方法：当条带为XX、XY型条带时，若条带内含有矩形件的数量为奇数，则自条带左上角水平向右开始进行“之”字型切割分离矩形件；若条带内含有矩形件的数量为偶数，则自条带左上角竖直向下进行“之”字型切割分离矩形件。当条带为YX、YY 型条带时，若条带内含有矩形件的数量为奇数，则自条带左上角竖直向下进行“之”字型切割分离矩形件；若条带内含有矩形件的数量为偶数，则自条带左上角水平向右进行“之”字型切割分离矩形件。条带间分离具体切割方法：当条带为XX、XY 型条带时，自左向右直线分离条带；当条带为YX、YY 型条带时，自下而上直线分离条带。

假设条带内含有第i种矩形件的数量为a，则条带切割路径长度C(a)的计算方法如下：

当a为奇数时：

当a为偶数时：

一张板材的切割路径长度为其上所布局条带切割路径长度之和；下料方案的切割路径长度为其所用板材切割路径长度之和。

3 算法设计与实现

SVC框架在求解下料问题时得到广泛应用[12-13]。本文将基于价值修正的顺序启发式算法与排样方式生成算法相结合，形成下料方案的生成算法。利用基于价值校正的顺序启发式算法多代、顺序、价值校正的特点，经多次迭代后，从多个下料方案中优选生产成本最小者作为最终下料方案。

3.1 下料方案生成算法

按照式（1）计算下料方案总成本，Gmax为最高迭代次数，G为当前迭代次数，ri为第i种矩形件的剩余需求量(i=1,2,…,m) ，bj为第j种板材的剩余库存量(j=1,2,…,n)，qi为排样方式所含第i种矩形件的数量(i=1,2,…,m)，f为排样方式的使用次数。下料方案生成算法步骤如下，其中GetPattern()函数和CorrectValue()函数将分别在3.2和3.3节中介绍。

步骤1令G=1，初始化毛坯价值ci=li×wi，i=1,2,…,m；令最佳下料方案的总成本为正无穷大。

步骤2如果G ＞Gmax，转步骤9，否则，令矩形件的剩余需求量等于初始需求量，即ri=di，令板材的剩余库存量等于初始供应量，即bj=Dj，其中i=1,2,…,m，j=1,2,…,n。

步骤3调用GetPattern()函数生成当前排样方式。

步骤4根据当前使用第j种板材(j∈[1,2,…,n])的库存量和需求量确定当前排样方式使用次数f，，更新矩形件剩余需求量ri=ri-fqi，更新板材库存量bj=bj-f，并将此排样方式加入当前下料方案中。

步骤5调用CorrectValue()函数修正矩形件的价值。

步骤6对于所有的矩形件，只要存在一个ri ＞0(i=1,2,…,m)则转步骤3，否则转步骤7。

步骤7计算当前下料方案的生产成本，若当前下料方案的生产成本低于目前最佳下料方案的生产成本，则更新最佳下料方案。

步骤8G=G+1。转步骤2。

步骤9输出最佳下料方案。

3.2 GetPattern()函数

构建前瞻法，采用同质条带多级规范布局方式，通过求解如下有界二维背包问题（6）确定当前板材的排样方式：

前瞻法即每伪布局一根条带，都要考虑剩余子板的所有布局可能性，并计算出其价值，最后以式（6）确定最终排样方式，示意图如图3所示，具体方法描述如下。

设lmin，wmin分别为矩形件尺寸中的最小长度和最小宽度，在尺寸为x×y的板材上生成同质条带多级规范布局方式，板材最大价值为F(x,y)，则递推公式如下：

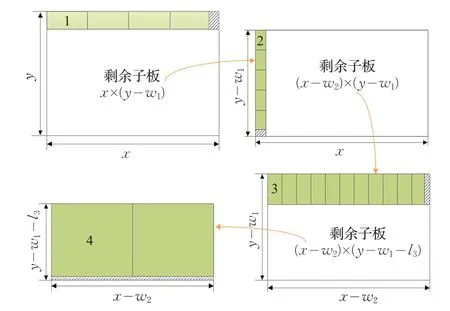
图3 前瞻法示意图

当x ＜lmin或y ＜wmin，同时x ＜wmin或y ＜lmin，F(x,y)=0。

否则，

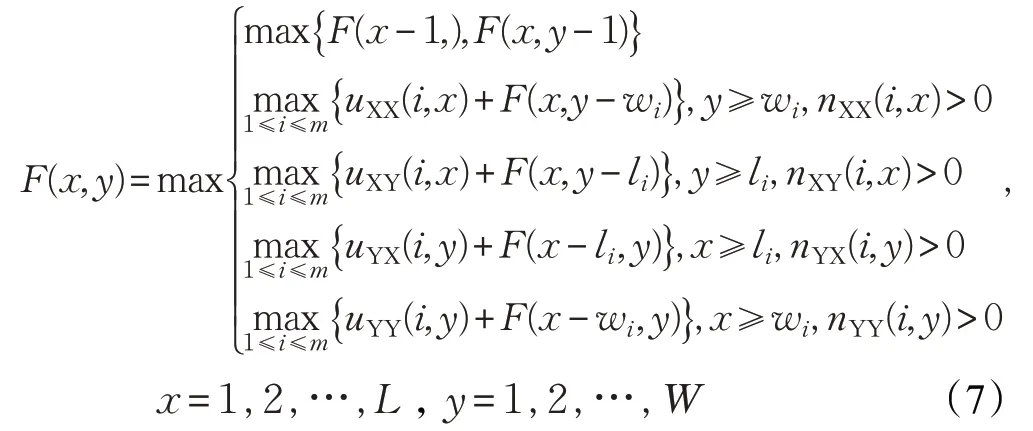
式（7）的时间复杂度为O(mLW)，而且其具有全容量特性：一旦计算出F(x,y) ，那么对于所有的x×y(x∈[1,L]⋃y∈[1,W])，F(x,y) 的值均已计算出来。即每一步根据F(x,y)的取值情况，可以确定板材x×y的排样方式。

设函数getPattern(x,y)返回当前排样板材最大价值，函数算法步骤如下：

步骤1令F(x,y)=0，i=1。

步骤2令VXX=0，VXY=0，VYX=0，VYY=0。若当前待排样板材x×y不能布局任何一种矩形件条带，则转步骤 5；否则：如果x≥li，而且y≥wi时，则令VXX=uXX(i,x)+getPattern(x,y-wi)，VYX=uYX(i,y)+getPattern(x-li,y)；若x≥wi且y≥li，令VXY=uXY(i,x)+getPattern(x,y-li)，VYY=uYY(i,y)+getPattern(x-wi,y)。

步骤3令V=max{VXX,VXY,VYX,VYY} 。

步骤4如果F(x,y)＜V，令F(x,y)=V。

步骤5令i=i+1。如果i≤m，则转步骤2。

步骤6返回F(x,y)。

在实际生成排样方式的过程中，初始化x=Lj，y=Wj(j=1,2,…,n)，依次调用函数getPattern(x,y)，得到每种可用板材最大价值的排样方式。根据2.3 节计算每种板材的切割路径长度，按下式计算板材的产出率：

以最高产出率确定最终使用板材种类及其排样方式。

3.3 CorrectValue()函数

下料方案生成算法中，每生成一个排样方式后，都对矩形件价值进行修正[12]，调整矩形件的优先级，解决局部最优问题，实现下料方案多样化。矩形件价值修正公式[14]如下：

其中，g1+g2=1；g2=εqi(di+ri)；参数ε∈[0.6,0.9]，默认值为0.75；ρ为略大于1的控制参数，默认值为1.02；U为当前排样方式利用率，。

4 实验结果与分析

本实验采用C#编程，实验用计算机配置为Intel Core i5-4590 CPU，3.3 GHz 主频，4 GB 内存。其中参数Gmax=500。

4.1 单一算例实验对比

采用文献[9]中的例题，仅有1组矩形件和1组板材尺寸（分别为500×400、800×600、1 000×800）。本文算法运行结果如图4所示，共有3个排样方式，每个排样方式使用次数为1、板材尺寸均为800×600，其中图4（d）中带箭头的红色实线表示分离矩形件的切割线，带箭头的蓝色虚线表示分离条带的切割线。本文算法与文献[9]算法材料利用率均为99.58%，切割总路径分别为36 180和36 660，前者小于后者，与后者相比前者切割总路径降低1.31%。由此可知，针对本算例，与文献[9]相比，本文算法在材料利用率相同的情况下，下料方案具有更短的切割路径和更高的生产效率。

图4 下料方案及排样方式切割路径图

4.2 多组算例实验对比

由于单一算例实验结果具有偶然性，为了进一步验证本文算法的有效性与可行性，从文献[15]中选取20道基准实例与文献[9]算法进行对比，其中每道题都有20组矩形件，5 种可供使用板材（尺寸分别为1 400×700、1 700×850、2 000×1 000、2 800×1 400 和4 000×2 000）。表2列出了本文算法与文献[9]算法的测试结果，其中U和CL分别代表本文算法的材料利用率和切割路径总长度，U1和CL1则分别代表文献[9]算法的材料利用率和切割路径总长度，ΔU和ΔCL分别表示材料利用率和切割路径总长度的差值，其中ΔU=U-U1，ΔCL=CL-CL1。从表中可以看出，两种算法的平均材料利用率分别为95.66%和88.62%，前者较后者提高7.04%；平均切割路径分别为83 218.8 和87 741.6，前者较后者减少4 552.8，与后者相比前者切割总路径降低5.19%。由数据对比可知，本文算法能够有效地降低生产成本，缩短下料时间，提高下料效率。

表2 两种算法的实验结果及对比情况

5 结束语

本文以材料利用率和切割成本为优化目标，提出一种面向可加工性的矩形件优化下料算法，其中算法以低割成本和高材料利用率为目标，建立了以生产成本（材料成本与切割成本之和）最小为目标函数的数学模型，模型中将下料过程中能源、加工工时、人力资源等消耗通过控制参数统一折算为切割成本，以生产成本最小为目标函数，简化了优化下料过程中相关环节的处理方法，对优化下料问题的研究具有重要意义。另外，最后通过实验对比证实本文提出的优化下料算法符合实际生产的需求，能在维持高材料利用率的同时，使下料方案具有较低的切割成本和良好的可加工性，提高下料效率，对于企业的长远发展具有重要意义。