受灾区域卫星遥感监测的条带分解方法研究

许友善，林广宏，赵 晗，谢亚恩

（1.中国船舶集团有限公司第七二二研究所，湖北 武汉 430200；2.中国船舶及海洋工程设计研究院，上海200011；3.哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨 150001）

引言

我国是自然灾害多发的国家之一，其灾害种类多、分布广、发生频率高、受灾损失严重。在轨卫星具有观测频次高、遥感范围广等特点，在灾害监测评估中发挥着重要的作用［6］。卫星遥感一直是森林草原火灾、雪灾、洪涝、地震等自然灾害的灾后监测和评估的重要手段。

由于受灾区域在灾后的监测条件复杂，传统的地面监测、气象卫星监测等手段很难实现对受灾区域的全面、高精度的监测，使得灾后救援难以有针对性地进行。因此，可以充分利用遥感卫星对受灾区域进行监测［1-5］。由于受灾区域面积较大，卫星幅宽有限，因此，用遥感卫星对受灾区域进行监测需要首先对受灾区域进行区域分解，使其能被卫星多次推扫覆盖。传统的卫星在轨观测任务规划通常为点目标规划，随着敏捷卫星的发展，卫星在轨机动能力的提升为大区域的条带拼幅成像提供了技术支持［7］。因此文中针对受灾区域灾后监测，给出了基于条带分解的敏捷卫星灾后快速监测方法，能够有效分析单颗敏捷卫星对受灾区域的覆盖观测时长，为各种自然灾害的灾后救援工作提供了数据支撑。

1 数学模型

1.1 集合和参数设计

定义T={v1,v2,...,vN}表示待观测的受灾区域，vi表示目标区域的第i个顶点，N表示目标区域的顶点数量；S={Si|Si=(a,e,i,Ω,ω,tp)}，表示卫星的集合，每个卫星对应一组轨道六要素，a,e,i,Ω,ω,tp分别表示卫星的轨道半长轴、轨道偏心率、轨道倾角、升交点赤经、近地点幅角、近地点时刻；LLA={LLAi|LLAi=(loni,lati),1 ≤i≤Norbit}表示预报的卫星轨道星下点经纬度数据集合，Norbit表示预报的卫星轨道点数；PV={PV1,PV2,...,PVNorbit}表示预报的卫星轨道位置和速度数据。Width表示卫星的视场幅宽；Cover表示相邻条带边缘所需的重叠宽度。

1.2 变量设计

m表示进行条带划分时，将目标区域沿垂直于星下点的方向均等分成m个条带；Strip={strip1,strip2,...,stripm}表示划分后的条带集合；stripj={vs,ve}表示第j个条带划分后得到的观测起始点和结束点；W={W1,W2,...,Wm} 表示计算得到的所有条带的成像时间窗口；Wj={tjs,tje} 表示卫星对条带stripj的实际成像时间窗口，tjs、tje分别表示实际成像时间窗口的开始时刻、结束时刻；TM表示2次条带成像任务间机动时长；γj,k为二进制变量，表示条带stripj的执行情况，γj,k= 1表示条带stripj在第k轨被执行，否则γj,k= 0［8］。

2 条带分解

2.1 计算条带分解的参考直线

计算目标区域每个顶点与同纬度下每一轨卫星星下点之间的经度差，第k轨的经度差之和计算如下。

则可以得到所有轨道对应的经度差之和的集合{sum1,sum2,...,sumk,...,summ} ，sumk的最小值对应的轨道K即为参考轨道。

确定参考轨道后，可以根据目标区域所有顶点与参考轨道的经度差{Δlon1,Δlon2,...,ΔlonN} 判断区域与参考轨道之间的位置关系。若所有Δlon均大于零，则区域在参考轨道右侧且不与参考轨道相交，若所有Δlon均小于零，则区域在参考轨道左侧且不与参考轨道相交，若Δlon既有大于零的值也有小于零的值，则参考轨道穿过受灾区域，若有Δlon等于零，则表明有顶点位于参考轨道之上。

在区域所有顶点中寻找纬度最大值latmax和最小值latmin，则可以得到中间纬度。

在参考轨道第K轨中寻找latmiddle对应的星下点LLAmiddle作为条带分解的参考点，如图1中的点LLAmiddle。

图1 参考直线示意图Fig.1 Reference line of aera

找到LLAmiddle两侧的星下点LLA1、LLA2，将其转换到高斯坐标系得到P1=(x1,y1)、P2=(x2,y2（)后文中提到的x,y坐标均为高斯坐标系下坐标）则可以得到参考直线的斜率。

因此条带分解的参考直线可以写为：

2.2 确定条带边界线

确定条带边界线首先需要计算边界的平移量Δx，再根据边界平移量确定最终的条带数量m。图2 给出了条带边界平移量示意图，根据给定的卫星幅宽Width计算得到条带边界的平移量如下。

图2 条带边界平移量示意图Fig.2 Displacement of strip edge

计算所有顶点到参考直线的距离，找到距离最小值dmin和最大值dmax，从而计算得到条带的数量如下

确定条带边界线首先需要检查顶点顺序并重新排列顶点。若参考直线不穿过受灾区域，则判断v1是否为距离参考直线最近的点，若不是则找到最近的顶点vi作为第一个顶点并将原来的顺序进行如下调换（原顶点是按照顺时针顺序给出的）：

若参考直线穿过受灾区域，则参考图3，首先找到参考直线两侧距离最远的2个顶点v1,v4，在两点之中找到一个距离相对较近的点v4作为第一个点，同样按照上述方式对顶点顺序进行调整。

图3 参考直线穿过受灾区域示意图Fig.3 Reference line crossing disaster aera

在得到边界平移量和第一个顶点之后，即可得到每个条带边界的直线，此处v1指的是调整顺序后得到的第一个顶点。Δx的正负按照左加右减的原则确定，例如受灾区域在参考直线左侧，或参考直线穿过受灾区域且第一个顶点在直线右侧，条带边界线从第一个顶点开始依次向左平移Δx，则Δx为正。同理，若受灾区域在参考直线右侧，或参考直线穿过受灾区域且第一个顶点在直线左侧，条带边界线从第一个顶点开始依次向右平移Δx，则Δx为负。第一个条带边界线穿过第一个顶点，平行于参考直线，直线方程如下：

第2个条带边界线方程如下：

第j个条带边界线方程如下：

由于划分共得到m个条带，则条带边界共有m+ 1个。

2.3 确定条带的观测起始点和结束点

条带的观测起始点和结束点确定的垂直于参考直线的2 条边界线我们称其为起始边线和结束边线，条带的起始边线和结束边线可能经过条带中存在的受灾区域顶点，也可能经过条带边界线与受灾区域边界线的某一个交点，因此要确定条带的起始边线和结束边线，首先需要找到条带中两端边界线所有可能的经过的点。

首先找到条带中存在的受灾区域的顶点。依次判断每个条带与每个顶点之间的位置关系，得到每个条带中的顶点，若顶点位于某一条带边界线上，则两侧条带所考虑的受灾区域顶点中均包括该顶点，最终可以得到每个条带中的顶点集合Vertex={vertex1,vertex2,...,vertexm} 。其中，vertexj={v1,...,vi} ，vertexj也可能为空集，即条带中不存在顶点。

在确定条带中存在的受灾区域的顶点后，再找到所有区域边界线与条带边界线之间的交点。根据集合Vertex={vertex1,vertex2,...,vertexm} 可以确定每个顶点所在的条带，假设2个相邻的顶点vi和vi+1分别位于条带s1和s2中，则顶点vi和vi+1之间的条带边界线为

式中(s1,s2]表示条带边界线s1+ 1,s1+ 2,...,s2，2 个相邻顶点vi和vi+1之间共s2-s1个条带边界线。因此与受灾区域边界edgei有交点的条带边界线集合={strips1+1,...,strips2} 。

计算受灾区域边界edgei与条带边界线={strips1+1,...,strips2} 的交点，记录到每个条带的顶点集合Vertex={vertex1,vertex2,...,vertexm} 中。则顶点集合中包括每个条带中存在的受灾区域顶点和条带边界线与受灾区域边界的交点。

作一条过顶点v1并垂直于参考直线l0的直线L，直线方程如下：

计算每个条带中的所有顶点qp到直线L的距离，如图4所示：

式中，d的值可能小于零。

从大到小（考虑d的正负）对计算得到的某一条带中的所有d进行排序，找到d的最大值和最小值对应的2 个点，即为条带起始和结束两端直线需要经过的点。以图4 中的条带strip2为例，计算条带中的4个顶点与直线L的距离，由于顶点位于L两侧，因此d有正负，此处正负只表示方位。对4个顶点的d进行排序，则可以确定条带最上方和最下方的2个顶点为v5、q3。分别过v5、q3作垂直于l0的直线，并计算直线与条带边界线的交点，得到条带的4个顶点{point1,point2,point3,point4} ，取条带的起始边线和结束边线的中点为条带两端的观测起始点和结束点，则条带的观测起始点和结束点可以表示为

图4 条带两端顶点计算示意图Fig.4 Vertex calculation figure of strip

最后判断星下点的走向，以图1 中的LLAmiddle为t0时刻，则LLA1={lon1,lat1} 、LLA2={lon2,lat2} 分别对应t0- 1和t0+ 1时刻。

若lat1＜lat2，则卫星上行，则选取point01、point02中纬度较小的点为观测起始点，另一点为观测结束点，反之卫星下行，选取point01、point02中纬度较大的点为起始点，另一点为观测结束点。由于上述计算是在高斯坐标系中进行的，因此需要将得到的观测起始点和结束点转换为经纬度，得到条带stripj的观测起始点和结束点stripj={vs,ve}。最终计算m个条带的观测起始点和结束点，得到Strip={strip1,strip2,...,stripm}用作成像任务规划的输入。

3 成像规划

计算条带stripj的观测起始点的开始可见时刻，并作为条带stripj的实际观测开始时刻tjs。根据卫星的地速vg计算条带stripj的观测时长，具体计算如下：

式中P1,P2分别表示条带stripj的起始观测点和结束观测点在地固坐标系中的坐标。因此，当条带的实际观测开始时刻确定后，其实际观测的结束时刻为：

卫星的可见性如图5所示，本文假设卫星是敏捷卫星，轨道偏心率为0，卫星最近可对星下点进行观测，最远可观测到与卫星地球表面的切点。卫星可见性约束可以表述为0 ＜θ＜θmax，其中RE、RS分别表示地球半径和卫星半长轴。

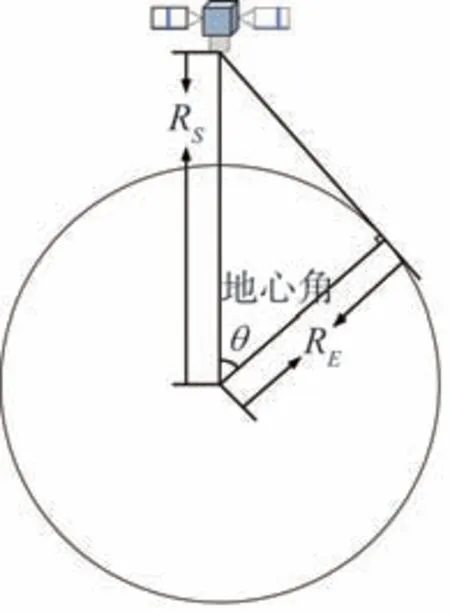
图5 卫星可见性示意图Fig.5 Satellite visibility figure

根据上述可见性约束，依次计算条带Strip={strip1,strip2,...,stripm}的可见性。

遍历卫星的LLA数据，计算卫星与目标间的地心角θ，若0 ＜θ＜θmax，则当前时刻卫星对目标可见，并以当前时刻作为条带stripj的实际观测开始时刻tjs，并可以通过式（17）计算得到条带stripj成像结束时刻。重复上述方法依次计算每个条带的实际成像时间。但是在计算每个条带的实际成像时间时，还需要考虑任务间的冲突，即条带stripl的成像时段对于已规划的任务序列中的任意其他条带stripj应满足tls-TM≥tje或tle+TM≤tjs。

最终，遍历所有条带，计算得到整个受灾区域的所有条带的实际成像时间窗口W={W1,W2,...,Wm} 。

4 仿真验证

4.1 仿真场景设计

表1 给出了仿真用到的卫星轨道参数。卫星的轨道预报时长为24 h，步长为1s，图6 中的曲线即为卫星的所有星下点轨迹。卫星的视场幅宽Width= 60 km，相邻条带边缘所需的重叠宽度Cover= 2 km。

表1 卫星轨道参数Table 1 Orbital parameters of satellite

（1）仿真场景1

考虑到四川地区自然灾害频发，因此在四川附近地区选取一个五边形区域作为受灾区域1，表2给出了目标区域1的顶点，图6给出了受灾区域1与轨道的示意图。

表2 目标区域1顶点Table 2 Vertex of disaster aera 1

图6 轨道与受灾区域1示意图Fig.6 Orbit and disaster aera 1

图7 轨道与受灾区域2示意图Fig.7 Orbit and disaster aera 2

（2）仿真场景2

为验证算法在处理受灾区域与卫星下点不同位置关系下的准确性，设计一种受灾区域位于星下点两侧的仿真场景，表3给出了目标区域的顶点，图6给出了受灾区域与轨道的示意图。

表3 目标区域2顶点Table 3 Vertex of disaster aera 2

4.2 仿真

（1）仿真场景1计算结果

图8 给出了条带计算结果，图9 给出了条带实际成像时段规划结果示意图。在不考虑轨道机动的情况下，以本文算例给出的轨道初始条件，得到的所有条带的最早成像时刻为19842 s（5.511 h），成像结束时刻为21 003 s（5.834 h），从开始成像到成像结束共耗时1 161 s（0.323 h），其中成像时长共1 004 s（0.279 h），任务间的机动及等待成像共耗时157 s。

图8 受灾区域1条带分解结果Fig.8 Strips splitting result of disaster aera 1

图9 受灾区域1成像时段Fig.9 Imaging time result of disaster aera 1

（2）仿真场景2结果

图10 给出了条带计算结果，图11 给出了条带实际成像时段规划结果示意图。在不考虑轨道机动的情况下，以本文算例给出的轨道初始条件，得到的所有条带的最早成像时刻为19 991 s（5.553 h），成像结束时刻为20 951 s（5.820 h），从开始成像到成像结束共耗时960 s（0.267 h），其中成像时长共820 s（0.228 h），任务间的机动及等待成像共耗时140 s。

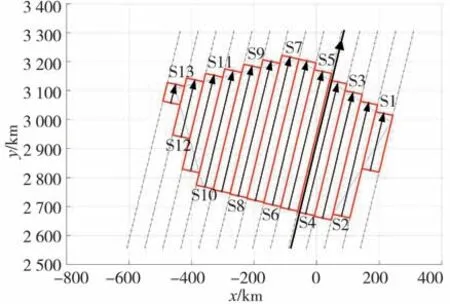
图10 受灾区域2条带分解结果Fig.10 Strips splitting result of disaster aera 2

图11 受灾区域2成像时段Fig.11 Imaging time result of disaster aera 2

5 结论

针对灾后小范围区域观测，气象卫星则难以满足精度要求的问题，文中给出了基于条带分解的受灾区域卫星遥感观测方法，提供了灾后小范围区域的观测思路。通过将受灾区域进行条带分解，使敏捷遥感卫星能够对受灾区域进行单轨连续观测或多轨连续观测，从而达到对受灾区域的灾后应急观测的目的。本文通过仿真算例，验证了本文给出的基于条带分解的区域目标的成像时段的规划方法，算法可行有效，为灾后小范围区域的灾后监视提供了参考。