一种二元矩阵值Padé型逼近的递推算法

王冬银, 开小山, 陶有田

(1.巢湖学院 数学与统计学院,安徽 巢湖 238000; 2.合肥工业大学 数学学院,安徽 合肥 230601; 3.巢湖学院 工商管理学院,安徽 巢湖 238000)

设f(x,y)为关于x,y的矩阵值形式幂级数

f(x,y)的二元矩阵值Padé型逼近(bivariate matrix-valued Padé type approximation, BMPTA)有着比较长期的研究历史,并在很多领域都有应用[1-4]。很多学者给出了许多有价值的研究结果[5-9]。文献[5]定义了一种内积空间上的BMPTA,并给出2个递推算法:E-算法和Sylvester型算法;但是这2个算法的计算量都比较大。

本文研究一种更加简洁的计算BMPTA的算法。文献[10]定义了一种二元齐次数量值多项式(bivariate homogeneous orthogonal polynomials, BHOP)。在此基础上,本文定义二元张量积形式正交多项式(bivariate tensor product formal orthogonal polynomials, BTPFOP),并将其推广到矩阵值情形,得到矩阵值二元张量积形式正交多项式(bivariate matrix tensor product formal orthogonal polynomials, BMTPFOP)。为计算其系数,本文给出三项及九项递推公式，通过这2个公式得到计算BMPTA的递推算法。最后,通过一个数值例子,验证了该算法的有效性。

1 二元数量值形式正交多项式

本节定义基于BHOP的BTPFOP,并研究其递推算法。

1.1 一元张量积正交多项式

设P是一个二元实多项式集,Pmn∈P。

定义1(BHOP)[10]若存在非零泛函σ,使得:

〈σ,PmnPkl〉=0,m+n≠k+l

(1)

则称{Pmn}为齐次弱正交多项式族。若

〈σ,PmnPkl〉=Kmnδmkδnl,

其中

则称{Pmn}为齐次正交多项式族。(1)式可写为：

〈σ,PmnPkl〉=0,k+l≤m+n-1

(2)

设cij是给定的实序列,定义P上的实线性泛函φ如下:

φ(sitj)=cij,i,j=0,1,…,

则φ完全由cij确定。将(2)式中的条件进行调整,并结合泛函φ,可得到下面的定义。

定义2 若一族二元多项式{vkl(s,t)}满足如下条件:

(1)vkl(s,t)关于s和t的最高次数分别为k和l,记为degs(vkl)=k,degt(vkl)=l。

(2)φ(sitjvkl)=0, (i,j)∈{(i,j)|

i=0,1,…,k;j=0,1,…,l}{(k,l)}

(3)

则称vkl为关于泛函φ的BTPFOP。

若vkl和vij((k,l)≠(i,j))是定义2中的形式正交多项式,则有φ(vijvkl)=0成立。

(i′,j′)∈{(i′,j′)|i′=0,1,…,k;

j′=0,1,…,l}{(k,l)}

(4)

记方程组(4)的Hankel-Hankel行列式为:

1.2 二元形式正交多项式的递推公式

定理1若泛函φ有定,则形式正交多项式族{vkl}线性无关。

证明对于k,l≥0,vkl(0,0)≠0,设存在一组常数λ00,…,λ0l,…,λk0,…,λkl,…, 使得:

(5)

在(5)式两端同时作用泛函φ,可得:

λklφ(vklvkl)=0。

又因为φ(vklvkl)≠0,所以对∀k,l≥0,λkl=0。故{vkl}线性无关。

利用一元数量值形式正交多项式的三项递推公式[10],不加证明地给出:当k≥0,l=0和k=0,l≥0时,BTPFOP的三项递推公式。

引理1(BTPFOP的三项递推公式) 形式正交多项式vkl满足的递推关系如下:

k=0,1,…

(6)

初始值v-1,0=0,v00=1;其中

且有：

l=0,1,…

(7)

初始值v0,-1=0,v00=1;其中

对于一般的k,l≥0,可以得到下面的BTPFOP的九项递推公式。

定理2 形式正交多项式vkl满足的递推关系如下:

vk+1,l+1=-Ak+1,l+1vk+1,l-Bk+1,l+1vk+1,l-1-

Ck+1,l+1vk,l+1+(Dk+1,l+1st-Gk+1,l+1vk+1,l-1)vkl-

Jk+1,l+1vk,l-1-Kk+1,l+1vk-1,l+1-

Lk+1,l+1vk-1,l-Sk+1,l+1vk-1,l-1

(8)

初始值v-1,l=0,vk,-1=0;vk0、v0l由引理1计算,其中的系数关系式如下:

证明由定理1知,{vkl}是P的一组基,因此stvkl可以唯一地表示为{vkl}的线性组合:

(9)

在(9)式两端同时乘以vij并作用泛函φ,可得:

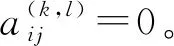
当i=k-1,j=l-1时,

当i=k-1,j=l时,

当i=k-1,j=l+1时,

当i=k,j=l-1时,

当i=k,j=l时,

当i=k,j=l+1时,

当i=k+1,j=l-1时,

当i=k+1,j=l时,

当i=k+1,j=l+1时,

若对于首一多项vkl,即对∀k,l≥0,bkl=1,则(8)式中的Dk+1,l+1=1。

2 二元矩阵值形式正交多项式

φ(μ,ν)(sitj)=ck+i,l+j∈Cp×q,i,j,μ,ν≥0

(10)

其中,cij=0,i<0或j<0。

定义3 若多项式族{Vkl(s,t)}满足下面的的条件:

(1) deg(Vkl)=(k,l)。

(2)φ(μ,ν)(sitjVkl)=0,(i,j)∈{(i,j)|

i=0,1,…,k;j=0,1,…,l}{(k,l)}

(11)

则称{Vkl(s,t)}为关于泛函φ(μ,ν)的广义形式正交多项式。

由条件(1),bkl≠0，此时称泛函φ(μ,ν)是有定的。设

(12)

由(11)式,可将(12)式化为一个方程组:

(i′,j′)∈{(i′,j′)|i′=0,1,…,k,

j′=0,1,…,l}{(k,l)}

(13)

其中,系数cμ+i+i′,ν+j+j′是矩阵值。为了计算bij,利用矩阵的直接内积将cμ+i+i′,ν+j+j′转化为数量值。设X=(xij),Y=(yij)∈Cp×q,则矩阵X、Y的直接内积定义为：

将矩阵e∈Cp×q和泛函φ(μ,ν)的直接内积写为〈e,φ(μ,ν)〉,其中,eij=1。记

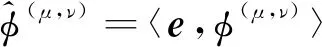
(14)

定义4 若多项式族{vkl(s,t)}满足下面的条件:

(1) deg(Vkl)=(k,l)。

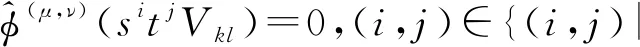
i=0,1,…,k;j=0,1,…,l}{(k,l)}

(15)

由(15)式，可将Vkl(s,t)化为如下形式：

(i′,j′)∈{(i′,j′)|i′=0,1,…,k;

j′=0,1,…,l}{(k,l)}

(16)

引理2(BMTPFOP的三项递推公式) 形式正交多项式Vkl满足的递推关系为:

k=0,1,…

(17)

初始值V-1,0=0,V00=1。其中

且有：

l=0,1,…

(18)

初始值V0,-1=0,V00=1。其中

与定理2的证明类似,可以得到BMTPFOP的九项递推公式。

定理3(BMTPFOP的九项递推公式)

Vk+1,l+1=-Ak+1,l+1Vk+1,l-Bk+1,l+1Vk+1,l-1-

Ck+1,l+1Vk,l+1+(Dk+1,l+1st-Gk+1,l+1Vk+1,l-1)Vkl-

Jk+1,l+1Vk,l-1-Kk+1,l+1Vk-1,l+1-

Lk+1,l+1Vk-1,l-Sk+1,l+1Vk-1,l-1

(19)

初始值V-1,l=0,Vk,-1=0;Vk0、V0l由引理2计算,其中的系数由以下关系确定:

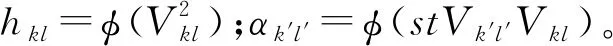
3 BMPTA的递推算法

设矩阵值函数f(x,y)具有形式幂级数

为了表达方便,下面将文献[5]中BMPTA的定义进行改写。在(10)式和(14)式中,取μ=n1-m1+1,ν=n2-m2+1,则有：

φ(n1-m1+1,n2-m2+1)(sitj)=cn1-m1+1+i,n2-m2+1+j,

〈e,φ(n1-m1+1,n2-m2+1)〉=〈e,cn1-m1+1+i,n2-m2+1+j〉,

其中,cij=0,i<0或j<0。

设Vm1m2(x,y)是形式多项式

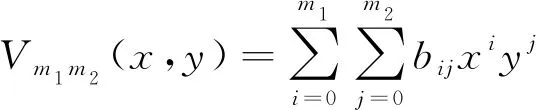
(20)

显然有bm1m2≠0。定义二元矩阵值多项式:

Wn1n2(x,y)=φ(n1-m1+1,n2-m2+1){[Vm1m2(x,y)+

Vm1m2(s,t)-Vm1m2(s,y)-Vm1m2(x,t)]/

(s-x)(t-y)}

(21)

其中，泛函φ(n1-m1+1,n2-m2+1)作用在s、t上。设

(22)

(23)

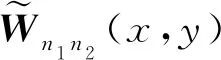
(24)

证明由(21)式得：

Wn1n2(x,y)=

再由(23)式得:

(25)

BMPTA的递推算法步骤如下：

(1) 取初值V-1,0=V0,-1=0,V00=1。

(2) 由(17)式计算Vk0,k=1,2,…,m1。

(3) 由(18)式计算V0l,l=1,2,…,m2。

(4) 取初值Vk,-1=V-1,l=0,k=1,2,…,m1;l=1,2,…,m2。

(5) 由(19)式计算Vkl,k=1,2,…,m1;l=1,2,…,m2。

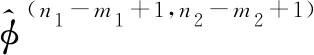
即

(26)

其中,(i′,j′)∈{(i′,j′)|i′=0,1,…,m1;,j′=0,1,…,m2}{(m1,m2)}。

相比于文献[5]中的E-算法和Sylvester型算法,本文的递推算法更加简洁。

下面通过一个数值实例来说明本文算法的有效性。已知

由(17)式可得:

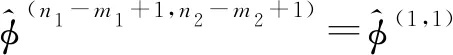
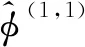
V10=x-1/2，V01=y-1/2。

于是可计算出以下系数:

进而有：

V11(x,y)=xy-A11V10-C11V01-G11=

因此得:

4 结 论

本文针对一种二元矩阵值Padé型逼近(BMPTA)给出了一个简洁的递推算法。根据二元齐次数量值正交多项式,定义了二元张量积形式正交多项式(BTPFOP)和二元矩阵值张量积形式正交多项式(BMTPFOP),并给出了BMTPFOP的三项递推公式及九项递推公式。基于这2个公式,得到了计算BMPTA的递推算法,并举例说明了该算法的有效性，但并没有给出其误差估计。因此,该方法对于二元矩阵值函数f(x,y)的误差估计有待进一步研究。