基于Taguchi实验分析的狼群算法在贴片机上的应用

倪郁东, 曾志超, 杨晨罡, 杨 航, 高丽杰, 夏仕伟

(合肥工业大学 数学学院,安徽 合肥 230601)

贴片机是整条精密电子组装生产线上完成贴装操作的关键设备,其生产效率会影响整条生产线的生产能力发挥,因此必须提高贴片机的装配速度才能缩短装配时间、提高效率,从而增产。而贴片机的装配速度往往与其贴装过程有关。

通常贴片机贴装过程的优化问题可分解为2个相互关联的子问题:喂料器的分配问题和元器件的贴装顺序问题[1]。这2个问题均为NP-hard问题,同时解决相当困难。由于贴片机贴装工艺问题具有高维数、离散及非线性的特点[2],用传统优化方法很难求得全局最优解,因此启发式算法成为求解此类问题的一种新方式。文献[3]根据问题的特点提出了二维分段式的十进制编码,并在遗传算法操作过程中运用改进的顺序交叉和自适应的变异操作,实现了贴装顺序和供料槽布置的同时优化;文献[4]提出了一种免疫算法,该算法通过设计合理的问题编码、免疫算子以及参数来优化多头拱架式贴片机的贴装过程;文献[5]采用启发式最近邻类方法优化初始种群,从而改进了蛙跳算法,实现了贴片机的贴装过程优化,实验结果表明,采用改进蛙跳算法后能更快、更精确地收敛于问题的全局最优解。此外,对于贴装优化问题的求解还有蚁群算法[6]、蝙蝠算法[7]、伞布搜索算法[8]等智能算法。

狼群算法是由文献[9]提出的一种新型智能算法，该算法具有收敛速度快、寻优精度高、寻优方式灵活等优点[10]。本文采用狼群算法解决贴片机的贴装过程优化问题,并对其离散化以适合贴片机的分组贴装;为加快收敛速度、提高求解精度,对离散化后的狼群算法加以改进,采用Taguchi正交实验优化算法中的关键参数;结合多头拱架式贴片机的特点,建立以最小化贴装时间为目标的贴装优化数学模型,并给出一组保证贴装序列无循环的充要条件;对建立的模型用改进离散狼群算法求解,实验结果证明了本文改进离散狼群算法是有效的。

1 多头拱架式贴片机

多头拱架式贴片机示意图如图1所示。对于给定的贴装序列,贴装头从起点出发移到喂料器左端,再向右移吸取元器件;吸满后移到印刷电路板(printed circuit board,PCB)上,按刚才吸取顺序贴装;贴完后再回到喂料器左端,此时完成1次贴装循环,即吸取—位移—贴装—位移。贴装头不断重复这样的贴装循环,直到贴装序列上的元器件都被贴完,回到起点。

图1 多头拱架式贴片机示意图

2 贴装优化数学模型

2.1 模型假设

贴片机贴装过程的优化问题属于NP-hard问题,要完全解决相当困难。为凸显贴装过程的核心问题及适当简化模型,须去掉些不必要的环节。为此,作出如下假设:元器件类型及分配已确定;在喂料器上取料、PCB上单点贴装的时间为定值,可忽略;贴装时不换吸嘴,即不考虑换吸嘴所费时间;贴装头匀速移动,不考虑加速、减速运动;贴元器件前的机器视觉识别、矫正时间为定值,可忽略。

2.2 符号说明

2.3 贴装决策变量

为准确描述贴装过程,下面定义模型中用到的0-1决策变量:

xij表示元器件贴装顺序。当i=j时,xij=0;当i≠j时,若贴完i号元器件后贴j号元器件,则xij=1;否则xij=0。

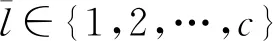
2.4 贴装优化数学模型的建立

贴装时间的短长直接反映了贴装效率高低,本文建立以最小化贴装时间为目标的贴装优化数学模型。记第1个贴的元器件编号为a,a∈{1,2,…,n}。目标函数及约束条件为:

(1)

(2)

(3)

λ1=λ2=…=λn=0

(4)

其中,λ1,λ2,…,λn为贴装序列对应矩阵X=[xij]n×n的全部特征根。

约束条件(1)～(4)式为保证贴装序列不出现循环的充分必要条件。

2.5 模型约束条件充分必要性的证明

定理1 对满足约束条件(1)～(3)式的贴装序列,其无循环的充分必要条件为约束条件(4)式。

(1) 必要性。设无循环贴装序列为w1→w2→…→wn,其中w1,w2,…,wn为元器件编号,是1,2,…,n的一个排列。由排列理论可知,任一排列都能经过一系列对换变为自然排列,而这些对换可以为相邻对换。根据相邻对换发生在贴装序列上的位置,可以分为开头、中间、末尾3种情况。下面选取相邻对换发生在贴装序列开头证明,另外2种情况类似可证。

相邻对换发生在贴装序列开头,即贴装序列w1→w2→w3→…→wn变为w2→w1→w3→…→wn。从决策变量看,xw1w2=1、xw2w3=1变为xw2w1=1、xw1w3=1。若记原贴装序列对应矩阵为A,发生相邻对换后的贴装序列对应矩阵为B,则有:

变为:

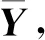
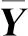
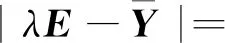
其中,E为单位矩阵。

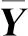
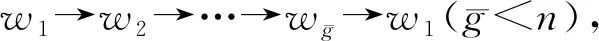
3 离散狼群算法

3.1 基本定义

设狼群狩猎空间为N×n维离散空间,其中N为种群规模,n为贴装序列元器件数。狼k的位置表示为Wk=(wk1,wk2,…,wkn),k=1,2,…,N,其中wk1,wk2,…,wkn为元器件编号,是1,2,…,n的一个排列;适应度记作Yk=f(Wk);狼与狼之间的距离定义为适应度差的绝对值。

(1) 对换Ω。交换狼k的wki号元器件和wkj号元器件(i≠j)的贴装顺序称为Wk的一个对换,记作Ω(wki,wkj)。

(2) 游走算子Θ。狼k游走方向定义为Wk的连续子序列Mh={wh1,wh2,…,whr},其中r为游走步长,其值等于子序列Mh的长度;易知,方向数h与游走步长r满足关系式h=n-r+1。游走算子Θ(Wk,Mh,r)表示狼k在方向Mh上连续游走r次,即作Wk的r次连续对换,具体的对换规则将在游走行为中叙述。

(3) 替换矩阵R。当i≠j时,R(i,j)表示到i号元器件与j号元器件距离和最小的元器件编号。当i=j时,R(i,j)表示到i号元器件与喂料器端点距离和最小的元器件编号。

3.2 智能行为描述

狼群算法包含“胜者为王”的头狼产生规则、“强者生存”的种群更新规则及游走、奔袭、围攻3种智能行为。前2个规则参见文献[9],下面叙述3种智能行为在贴装优化问题上的离散化过程。

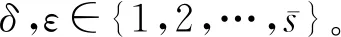
当头狼不再更新且每只猛狼与头狼适应度差的绝对值小于阈值uYlead时,奔袭行为结束。由于往往最优解的组内贴装序列相对较优,可见分组替换适合求解多吸嘴贴片机最优贴装序列。此外,阈值uYlead随迭代变小,可保证后期收敛速度。

(3) 围攻行为。接近猎物时,头狼带领探狼和猛狼一起进入围攻行为。具体地,对于狼k,从Wk中随机选取一个元器件(除各分组最后一个外),记其编号为wki,用它在头狼序列上的下一个元器件替换wki号元器件的下一个元器件。若新位置气味更浓,狼k向该位置前进。

3.3 算法改进

3.3.1 面向近邻概率的初始解生成

借鉴贪婪算法[11]与文献[12]的思想,本文提出一种适合贴片机分组贴装的面向近邻概率生成初始解的方法,该方法有利于加快狼群前期寻优、提高更新解质量,具体步骤为:

(1) 求距离矩阵D1。D1(i,j)表示i号元器件与j号元器件距离。

(2) 求距离矩阵D2。D2(i)表示i号元器件与喂料器端点距离。

(3) 求过渡近邻概率矩阵P1。P1(i,j)表示贴完i号元器件后贴j号元器件的概率。具体地,当i=j时,P1(i,j)=0;当i≠j时,

(4) 求过渡近邻概率矩阵P2。P2(i)表示选取i号元器件作为组第1个元器件的概率,计算公式为:

(5)

(5) 按2种情形产生初始贴装序列。

情形1 组第1个元器件。将P2的元素P2(1),P2(2),…,P2(n)从大到小排列,得到近邻概率矩阵P2′=[P2(j1)P2(j2) …P2(jn)],其中P2(j1)+P2(j2)+…+P2(jn)=1;j1,j2,…,jn是1,2,…,n的一个排列;再依概率选出组第1个元器件。

情形2 组内元器件。对于i号元器件,将P1的元素P1(i,1),P1(i,2),…,P1(i,n)从大到小排列,得到近邻概率矩阵P1′=[P1(i,j1)P1(i,j2) …P1(i,jn)],其中P1(i,j1)+P1(i,j2)+…+P1(i,jn)=1；j1,j2,…,jn是1,2,…,n的一个排列;再依概率选出i号元器件的组内下一个元器件,记其编号为j。若j号元器件非组内最后一个,则跳转到情形2,否则跳转到情形1。

对于情形1和情形2得到的近邻概率矩阵P(P=P1′或P=P2′),选择下一个元器件的最终概率计算公式为:

(6)

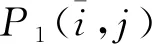
3.3.2 狼群分组行为

分组行为体现了狼群的分工与合作。一方面,多只头狼指导可避免陷入局部最优;另一方面,分组并行搜索能在一定程度上增大寻优概率。

3.3.3 头狼自我调整

(7)

4 Taguchi正交实验设计

4.1 Taguchi正交实验原理

Taguchi方法是重要的实验设计方法,能降低实验次数,选出合适参数[15]。该方法用正交表设计实验方案, 以信噪比作为评价质量稳定性的指标, 其实验结果可使质量更上乘、性能更稳定[16]。使用正交表可达到以较少实验次数选出较佳参数的效果,这使得Taguchi方法具有成本低、复杂度小的特点。

4.2 评价指标

(8)

(9)

(10)

5 实验与分析

5.1 对比实验分析

(1) 参数设计。为验证改进离散狼群算法的有效性,将其与未改进离散狼群算法、蜂群算法[17]作比较。实验中,种群规模为100,迭代次数为30,吸嘴数为4,其他参数选各自较优值。未改进离散狼群算法中,游走步长为3,奔袭步长为4,围攻步长为2,奔袭判停距离为3;改进离散狼群算法中,近邻上限数为3,狼群分组数为4,判停因子为0.05,替换概率pt=1/n;蜂群算法中,蜜源和跟随蜂数为种群规模1/2,放弃数阈值为5。

(2) 结果分析。生成5块20 cm×20 cmPCB作对比实验,对每块PCB使用3种算法均求解20次,取头狼适应度的最大值Ymax、最小值Ymin及平均值Yavg作比较,实验结果见表1所列。

表1 3种算法在5块PCB上的实验结果 cm

由表1可知,对于每块PCB,使用改进离散狼群算法得到的头狼适应度的最大值、最小值及平均值均最优,未改进离散狼群算法次之,蜂群算法最差,且结果差距随元器件数增多逐渐变大,这是由于改进离散狼群算法更适应贴片机的分组贴装。由此可知,改进离散狼群算法在寻优方面要强于未改进离散狼群算法和蜂群算法,整体求解水平也有所提高。

在求解效率上,改进离散狼群算法比未改进离散狼群算法平均提高3.18%,比蜂群算法平均提高16.67%。求解效率计算公式为:

(11)

综合上述分析可知,改进离散狼群算法适合求解规模较大的贴装优化问题。

为直观起见,分别画出元器件数为100、200时3种算法的贴装优化曲线,如图2所示。从图2可以看出,改进离散狼群算法在引入面向近邻概率生成的初始解后,由于更适应贴片机的分组贴装,在迭代初期相对于其他2种算法就已经获得了较高质量的解,这大大加快了求解速度;未改进离散狼群算法和蜂群算法前期收敛较快,但后期效果一般;从最后一代的适应度可以看出,改进离散狼群算法的求解精度要优于其他2种算法。

图2 不同元器件数下3种算法的贴装优化曲线

5.2 Taguchi实验分析

(1) 参数选取。在进行Taguchi实验前需选出影响算法性能的显著因素。本文选取的调优参数为:种群规模N、迭代次数ν、猛狼比例因子α、更新比例因子β及近邻上限数γ。N和ν越大,寻得最优解概率越大,但运行耗时变长且解质量改善速度减缓。奔袭行为中,由于头狼位置可能发生变化及猛狼奔袭步数的不确定性,其相对于游走行为和围攻行为更具有随机性,过高的α会使得求解不稳定,但合理的设置可以加快算法的收敛速度,提高较差个体适应度。种群更新规则可增加解的多样性,防止陷入局部最优,但过高的β不利于保证算法收敛速度。合理设置γ可以提高初始解和更新解的质量。

(2) 水平确定。狼群算法性能受参数取值影响,为确定各参数取值范围,采用控制变量法进行单因素实验。取N=100,ν=30,α=0.4,β=0.2,γ=3,以该参数取值组合为基准,分别改变N、ν及γ,观察其对头狼适应度的影响,进而确定取值范围;α、β根据其含义可知取值范围为0～1。实验时,每种参数取值均在2号PCB上求解10次。实验设计和结果见表2所列。

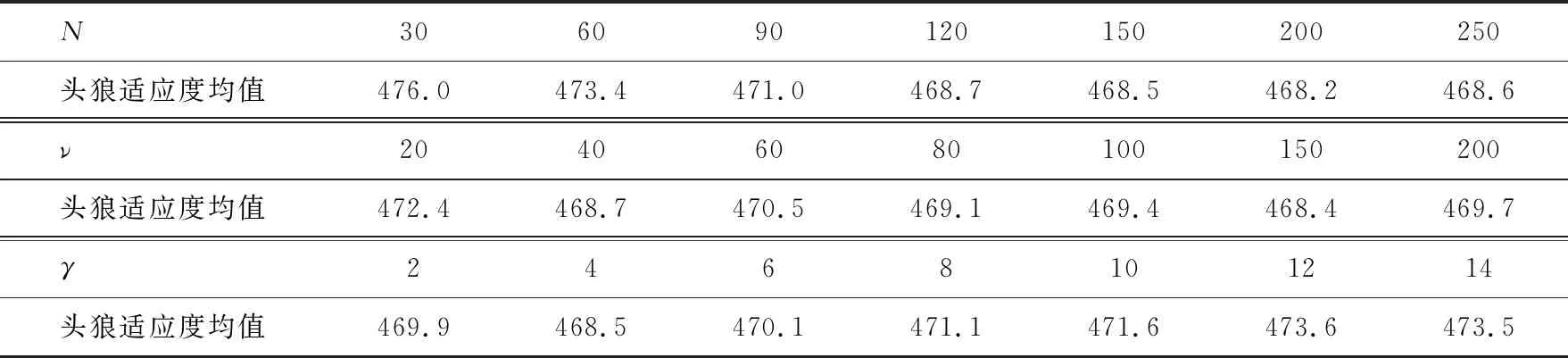
表2 N、ν及γ取不同值时的头狼适应度均值 cm

从表2可以看出,头狼适应度均值随N增大而减小,在取值区间[120,250]上,N对头狼适应度均值的变化无太大影响,故将影响显著的取值区间[0,120]作为N的取值范围;对于ν,有类似的结果,确定其取值范围为[0,100];当γ=4时,头狼适应度均值最小,而后随γ增大而增大,故将前部分取值区间[0,10]作为γ的取值范围。

5个参数在其取值范围内等间距选取4个水平,所得参数水平表见表3所列。

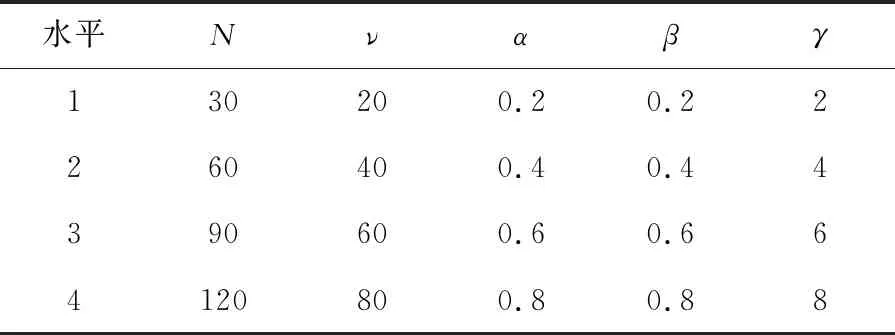
表3 五参数四水平表

(3) 正交实验方案。事实上,参数与参数之间往往存在关联,在确定5个参数的水平后,通过正交实验选出最优的参数水平组合。对于五参数四水平的正交实验,根据Taguchi方法原理可以选用L16(45)正交表,见表4所列。对正交表的16组方案在2号PCB上分别求解10次,得到头狼适应度后,再通过(8)式计算RSN,结果见表4所列。

表4 L16(45)正交实验方案

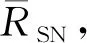
表5 5个参数在4个水平下的信噪比均值

从表5可以看出,N在水平3取得最大,ν在水平3取得最大,α在水平2取得最大,β在水平1取得最大,γ在水平1取得最大。为减小误差,现引入相对差η,计算公式为:

(12)

表6 参数待选水平组合与信噪比

根据表6,最终选取的参数水平组合为(3,4,2,1,1),即N=90,ν=80,α=0.4,β=0.2,γ=2。在最终选取的参数水平组合下,RSN与表4中最大的RSN接近,比较合理。

(5) 参数优化验证。为验证所选参数水平组合的有效性,使用改进离散狼群算法在该参数水平组合下对5号PCB求解20次,所得头狼适应度最大值为1 764.4 cm,最小值为1 735.6 cm,平均值为1 751.2 cm。结合表1可知,使用Taguchi正交实验优化后的参数,改进离散狼群算法的求解精度有所提高。

6 结 论

本文提出一种适合多头拱架式贴片机的改进离散狼群算法,并用其求解贴装优化数学模型。该算法通过引入面向近邻概率生成初始解的方法来提高初始解和更新解的质量,通过重新设计游走行为来增强全局搜索能力,通过狼群分组行动来维持种群多样性,最后采用Taguchi正交实验来优化算法中的关键参数。实验结果表明,本文提出的改进离散狼群算法在求解速度和求解精度上均优于未改进离散狼群算法和蜂群算法,适合贴片机的分组贴装,为解决贴片机贴装路径优化问题提供了新方法。后续工作将从理论上分析改进离散狼群算法的收敛性,尝试该算法在其他类型贴片机上的应用。