纯电动汽车ACC自适应权重优化策略

吴 迪, 朱 波, 张 农, 郑敏毅

(1.合肥工业大学 汽车工程技术研究院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

0 引 言

先进辅助驾驶系统(advanced driver assistance systems,ADAS)是指依靠车载传感系统进行环境感知并对驾驶员进行驾驶操作辅助的系统,常见的控制类子系统包括自适应巡航控制(adaptive cruise control,ACC)系统、自动紧急刹车等[1-2]。在ACC系统的设计中,目前采用较多的是依据车间时距进行期望安全车距模型的设计。固定车间时距(constant time headway,CTH)策略得到了广泛研究[3-6],但CTH策略有一些不足,当本车车速很高时需要和前车保持的车距过大,影响了道路利用率,也不符合驾驶员的实际驾驶习惯。基于时变车间时距(variable time headway,VTH)的安全车距模型考虑到了汽车驾驶环境状况对车间时距的影响,比CTH更加贴近实际情况。文献[7]通过大量试验研究了车间时距对ACC系统性能的影响,得出不同的车间时距更适用于不停变化的驾驶环境。

汽车控制及优化方面的研究很多[8-9],其中模型预测控制(model predictive control,MPC)由于能有效处理多个优化目标及约束,并能及时通过反馈来弥补模型失配,非常适用于ACC系统的控制策略设计。文献[10]在考虑驾驶员风格和道路交通特性的基础上提出了基于MPC的ACC系统;文献[11]基于模型匹配控制架构设计了MPC控制算法来提升ACC系统的跟随性能。MPC算法在运算时往往会出现非可行性解,因此研究人员也提出了相应的改进方法[12-14]。

本文以纯电动汽车ACC系统为研究对象,建立了车间纵向动力学模型,并提出了一种新的VTH策略,该VTH策略考虑了相对速度和不同驾驶员风格差异性的影响,并用饱和函数加以描述;设计了带有软约束的变权重自适应MPC控制策略,该控制策略可以在每个采样间隔依据自车和前车状态更新预测模型和控制目标的权重,从而能够更好地适应复杂多变的行驶环境;最后利用AMESim & Matlab/Simulink平台进行纯电动车整车建模和策略仿真验证,对提出的VTH策略和变权重模型预测控制(time-varying weight model predictive control,TW-MPC)策略与未优化的策略进行了性能对比。

1 车间纵向动力学建模

1.1 VTH车距模型

文献[15-16]研究了城市交通流模型及其相关信息,对其中驾驶员在稳态跟随工况下驾驶车辆的行为习惯参数进行了拟合,得到80%的数据分布在0.835～2.195 s内[16]。因此,在兼顾车辆安全性和道路通行能力的要求下,车头时距取2.5～3.0 s,较接近驾驶员在城市道路下的期望车头时距。将thmax=3.0 s作为车头时距th的上界,thmin=2.5 s作为车头时距th的下界,设计VTH模型如下:

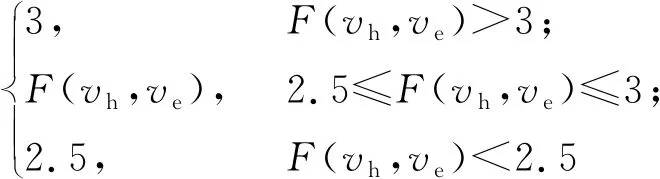
(1)

F(vh,vr)=tg+th1vh-th2ve

(2)

ddes=thvh+d0

(3)

其中,tg为驾驶员在人机交互界面可自行设定的基准车间时距;th1、th2为大于0的常数;vh为本车速度;ve为相对速度,即ve=vf-vh,vf为前车速度;ddes为期望跟驰车距;d0为绝对安全车距,即在两车消除相对速度后仍应保持的最小车距(本文设为5 m)。

1.2 车间纵向动力学模型

将车距误差、相对车速和本车加速度作为状态变量,前车加速度视为模型可测扰动,建立车间纵向动力学模型。由于电机和液压制动系统响应具有一定的延迟时间,在表示执行机构对期望加速度的响应时可以采用一个一阶系统,离散化后如下:

(4)

其中,ah(t)为在采样时刻t时本车的加速度;Ts为采样周期;KL为系统增益;τ为时间常数。KL、τ的具体数值可由频率响应法进行系统辨识得到[17],本文所研究的车辆模型KL=1、τ=0.5。

定义车距误差和相对车速为:

Δd(t)=dact(t)-ddes(t),

ve(t)=vf(t)-vh(t)

(5)

其中,dact为当前实际车距;ddes为期望车距;vf为前车车速;vh为本车车速。

建模时取状态变量x(t)和输出量y(t)如下:

x(t)=[Δd(t)ve(t)ah(t)]T

(6)

y(t)=[Δd(t)ve(t)ah(t)]T

(7)

将前车加速度视为模型可测扰动,即w(t)=af(t)。根据以上分析,建立车间状态空间模型为:

x(t+1|k)=Ax(t)+Buu(t)+Bdw(t)

(8)

y(t)=Cx(t)

(9)

其中

(10)

2 VCU控制策略设计

2.1 VCU控制系统设计

本文设计了自适应MPC控制器,下层控制包括车辆逆纵向动力学模型和制动力分配策略。所设计的整车控制器(vehicle control unit,VCU)系统结构如图1所示。

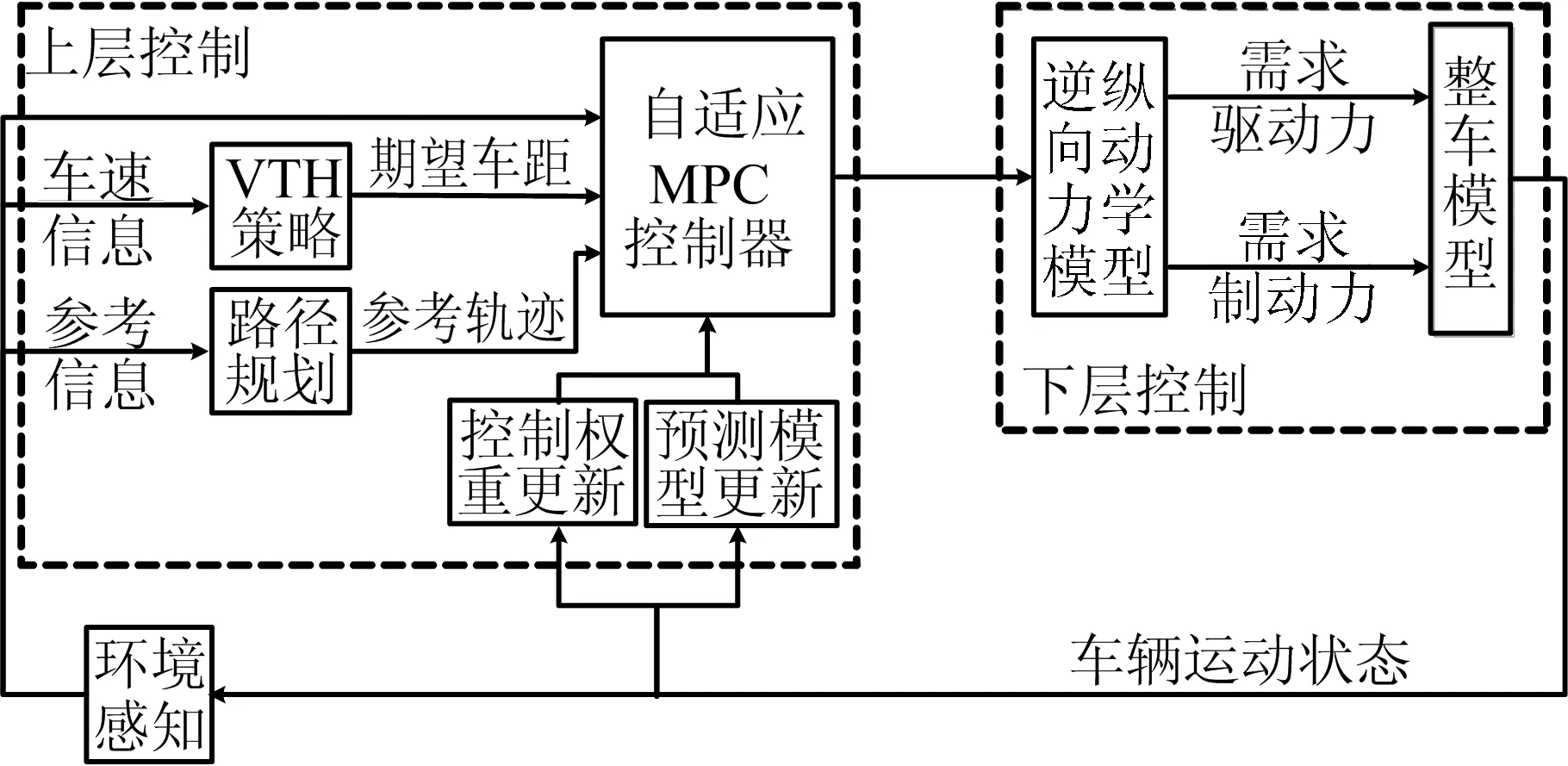
图1 VCU控制系统结构

图1中,环境感知包括车身传感器对于前车信息的获取处理和自车传感系统对于车辆运动状态信息的获取处理,其中前车和本车车速、本车加速度输出到自适应MPC控制器;车速信息(本车车速、相对车速)输出到VTH策略模块用于输出期望车距;参考信息(车距误差、相对车速、本车加速度)输出到路径规划模块用于生成参考轨迹。自适应MPC控制器根据所接收到的信息进行最优决策输出期望加速度。下位控制包括逆纵向动力学模型和整车模型,上位控制器决策出的期望加速度被转换成期望驱动/制动力控制车辆行驶。

2.2 自适应MPC控制器设计

本文设计的自适应MPC控制器可用于线性时变系统,同时考虑到了安全性、跟随性、经济性、舒适性。

系统安全性指的是在系统识别车辆处于紧急工况(如前车急刹车)时,应能及时有效地控制车辆紧急制动,以避免碰撞。因此,必须对实际车距施加一个硬约束,即

dact(t)≥dsafe

(11)

其中,dact为实际车距;dsafe为安全车距。本文依据碰撞时间理论[18]设计的安全车距如下:

dsafe=max(tcve,d0)

(12)

其中,d0为绝对安全车距,即本车与前车相对静止时应保持的最小车距,本文设为5 m;tc为碰撞时间,本文设为-2.7 s。

系统跟随性指的是本车能够良好地跟随前车,其控制目标为车距误差和相对车速均为0。设计车距误差和车速误差约束如下:

(13)

文献[19-20]提出系统经济性主要用车辆行驶过程的平顺性即加速度大小来衡量,车辆行驶过程中的加速度变化越平滑，整体经济性越高。在跟车过程中,行驶相同距离和相同平均速度下,加速度峰值越小,变化频率越低，经济性越好[19]。同时,系统舒适性也与加速度和冲击度密切相关,在跟车过程中车辆加速度和冲击度的大小越小，舒适性越好[20]。因此,经济性和舒适性的控制目标可描述为:

(14)

对车辆加速度和冲击度(加速度的变化率)做如下约束:

(15)

系统输出的参考轨迹设计如下:

yref(k+i)=Φiy(t)

(16)

其中,Φi=diag[φΔdφveφah]。φΔd、φve、φah分别为y(t)中各元素的衰减系数。

由(8)式、(9)式得到的目标函数和控制器约束存在一些缺陷[13]:① 目标函数无法对控制增量进行限制;② 由于控制器约束为硬约束,可能会导致因约束的上、下界固定不可逾越而不产生可行性解的问题,一般采用向量约束管理法解决该问题[14]。引入控制增量和约束因子对模型进行改进。同时应用卡尔曼预测器来预测系统在预测时域内的状态和输出。

引入控制增量后的预测模型如下:

(17)

(18)

其中,e(t)为t时刻系统输出预测误差(系统t时刻的实际输出与在t-1时刻预测的t时刻输出的差值);L为卡尔曼预测器中的误差增益矩阵,可通过求解黎卡提方程得到[9],即

(19)

其中，ex(t)为系统状态预测误差(系统t时刻的实际状态量与在t-1时刻预测的t时刻状态量的差值)。系统输出预测模型可描述如下:

SuΔU(t+i-1|t)+

SdW(t+i|t)+Γe(t)

(20)

其中

(21)

其中,Np为预测时域;Nc为控制时域,且Np≥Nc。假设控制量在控制时域之外保持不变。在采样时刻t时的系统干扰量可以由前一时刻即t-1时刻的本车加速度和相对速度估计得出,即

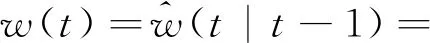
(22)

构建优化目标函数如下:

Q[y(t+i|t)-yref(t+i)]}+

(23)

其中,yref(k+i) 为(16)式设计的参考轨迹;Q为系统输出误差的权重矩阵;R为控制增量的权重矩阵;ε为引入的松弛因子;ρ为松弛因子惩罚系数。优化目标函数中第1项体现了对轨迹跟踪精度的要求,第2项体现了对控制增量变化幅度的要求,第3项是松弛因子的惩罚函数,惩罚系数可以约束松弛程度,避免松弛因子无限增大,也使控制器在可行性解和松弛程度中寻找平衡点。惩罚系数越大,松弛因子扩展约束的能力越弱; 反之,能力越强。

本文依据两车之间的行驶状态实时调节自适应MPC控制器的权重以提高系统的鲁棒性和更好的用户接受度。设计权重矩阵Q、R如下:

Q=diag[QiQi…Qi],

R=diag[RiRi…Ri]

(24)

其中,Qi=diag[wΔdwvewah],wΔd、wve、wah分别为对应于车距误差、相对速度、本车加速度的权重因子;Ri=wΔu,wΔu为对应于控制增量的权重因子。本文利用模糊控制来设计变权重因子系数的变化规则。以车距误差和相对车速为输入量,输入论域设为[-1,1];以4个权重因子的修正系数作为模糊控制器输出量,输出论域为[0,1]。模糊控制规则见表1所列。

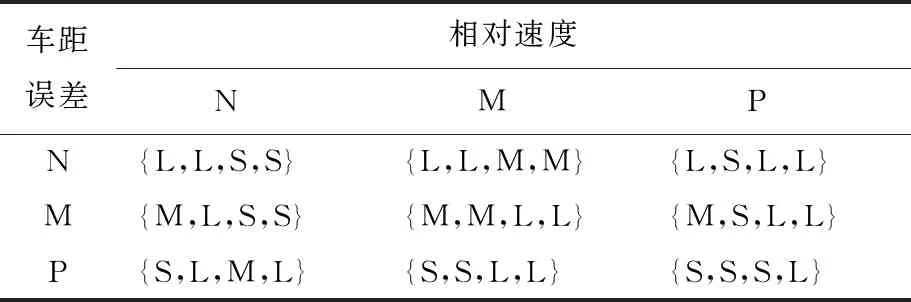
表1 权重因子系数规则

表1中规则量含义如下:N为“负”;M为“中”;P为“正”;L为“大”;S为“小”;M为“中”。由模糊控制器得到时变权重因子修正系数,时变权重因子的计算公式如下:

wΔd(t)=θΔdwΔd(0),wve(k)=θvewve(0),

wah(t)=θahwah(0),wΔu(k)=θΔuwΔu(0)

(25)

其中,θΔd、θve、θah、θΔu分别为模糊控制器输出的对应于车距误差、相对速度、本车加速度和控制增量的权重因子修正系数;wΔd(0)、wve(0)、wah(0)、wΔu(0)分别为各个权重因子的初值。综合考虑ACC系统的性能和工程调试经验,本文设置权重初值为{10,10,5,5}。

若降低安全性约束下界可能会发生碰撞事故,因此对于安全性下界不做松弛处理,而对于其他约束做松弛处理。对(13)式、(15)式做松弛处理后的约束如下：

(26)

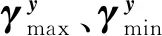
结合(2)式、(6)式、(11)式,系统时变安全性硬约束可表示为:

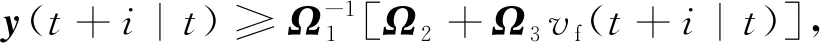
i=0,1,…,Np-1

(27)

其中

(28)

其中,dc为根据碰撞时间理论求出的安全车距,dc=tcve。由(27)式可知,该约束是一个时变约束,会随着车辆行驶环境的变化而不断更新约束矩阵,从而提高系统的鲁棒性。

因此,ACC系统的多目标优化问题是以(23)式为优化目标,(26)式、(27)式为约束的最优问题。自适应MPC在每个采样步长开始时依据两车相对运动状态更新预测模型和起始工作点,同时更新控制目标权重和系统安全性约束,这些更新量在预测时域内保持不变;然后控制器对优化问题进行求解,得到了一系列的控制序列,将该序列的第1个元素与上一时刻的控制量相加作为当前时刻的控制量,系统执行这一控制量直到下一采样间隔。在新的采样间隔开始时,系统又得到了新的状态信息,通过反馈校正和更新预测模型、约束和权重,再次求解得到了新的控制序列,如此循环往复即为自适应MPC控制器的工作过程。在应用中可将该优化问题转化为带约束的二次规划问题,可用积极集法或内点法求解。

3 仿真实验及分析

在AMESim&Matlab/Simulink联合仿真平台上进行仿真验证,整车仿真参数见表2所列。

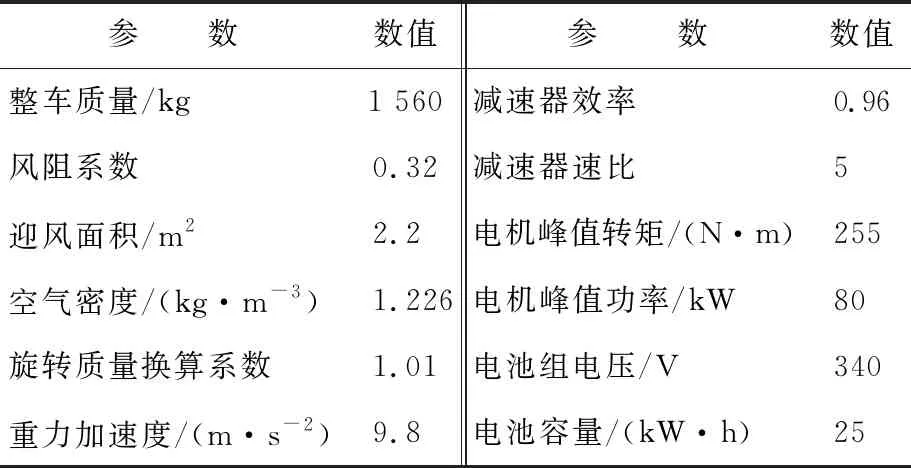
表2 整车模型参数

为了验证所提出的TW策略的有效性,设计目标函数权重为常数的CW-MPC控制器和采用时变权重策略的TW-MPC控制器,权重系数由模糊控制器决策得到。仿真场景设置如下:仿真时间共50 s,本车初始车速为60 km/h,前车以50 km/h的速度切入本车同车道前方50 m处,然后车速成正弦波动行驶,30 s时开始减速直至车速为0后停止行驶。该仿真场景涵盖了日常行车中的前车切入情况、减速跟车情况、稳定跟车情况和前车减速情况。仿真结果如图2所示。

从图2可以看出,由于TW-MPC策略的目标函数权重能够实时更新,车辆表现出了较好的性能,如TW-MPC控制策略下的车辆在减速跟车阶段车速波动较小,能很快使相对速度减小到较小范围,同时车辆加速度较为稳定(-0.8～0.2 m/s2),乘坐舒适性也较好;而CW-MPC控制下的车辆车速存在波动,而且加速度为-2.1～1.1 m/s2,表现出了较差的舒适性和经济性。

将仿真结果做量化统计,结果见表3所列。

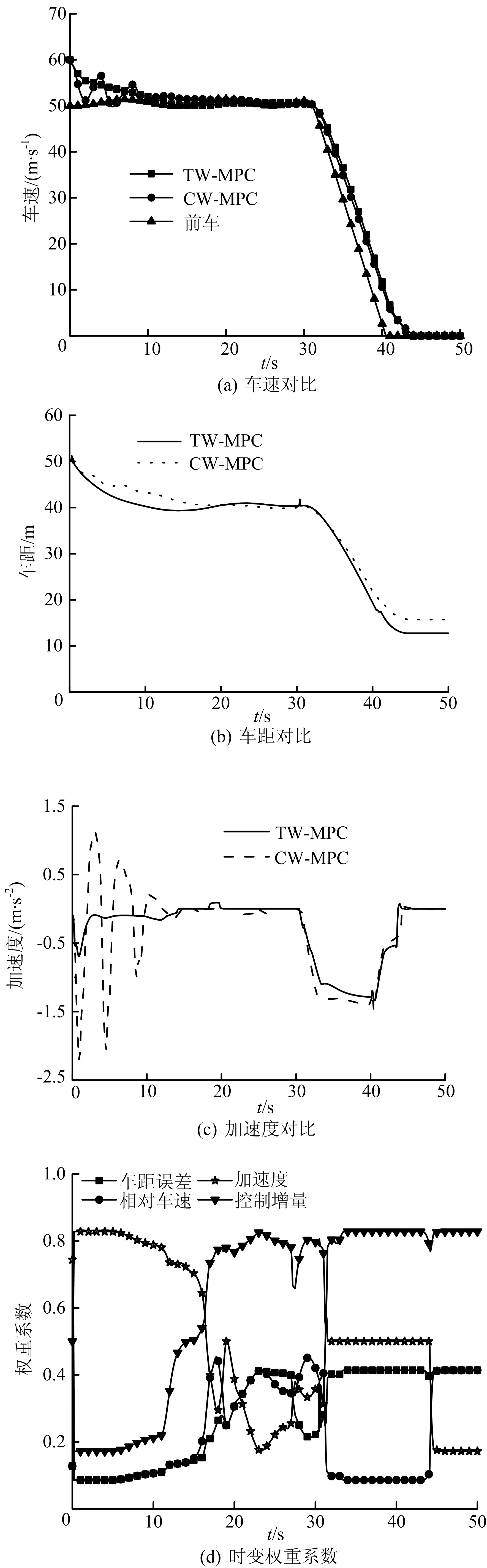
图2 仿真结果

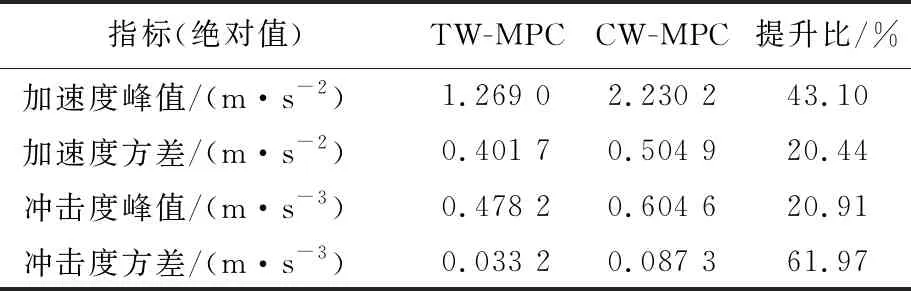
表3 经济/舒适性对比

由表3可知,采用TW-MPC策略的车辆加速度峰值大幅度减少,并且加速度稳定性也提升了约20%;同时车辆冲击度峰值和方差也有较大改善,表明车辆行驶更加平稳,舒适性和经济性也有了较大提升。

为了验证本文所提出的控制策略,利用以dSPACE和ESR毫米波雷达为核心搭建的辅助驾驶硬件在环实验平台进行实车试验。

在合肥市包河区某平直道路上进行试验,目标车位于试验车同车道前方,在驾驶员控制下以约30 km/h的速度匀速行驶,当试验车ACC系统启动时目标车开始加速,一段时间后开始减速。试验车在驾驶员控制下从目标车后方以高于目标车匀速行驶速度的车速行驶,开启ACC系统后驾驶员不再干预车辆行驶,以ACC系统开启时刻为起始时刻记录数据,直到车辆停止。试验场景包含了日常行车场景中的前车加速、减速和静止目标避撞控制过程。

为了验证所提出自适应权重策略的优越性,在该场景下分别作了2次试验,第1次试验中本车采用本文所设计的辅助驾驶系统控制策略,第2次试验中试验车控制目标权重策略采用固定权重CW策略用作对比试验,其他策略与第1次试验相同,同时在第2次试验中需要保持当ACC系统开启时的初始条件尽量与第1次试验一致,以做到更好地对比。

对比试验结果如图3所示。

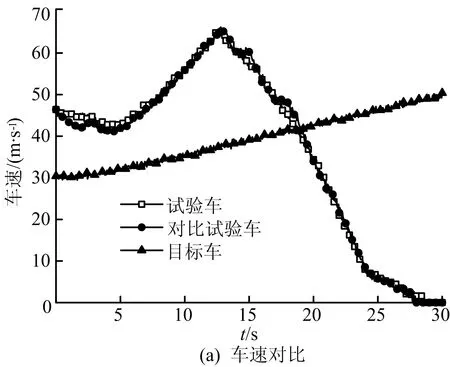
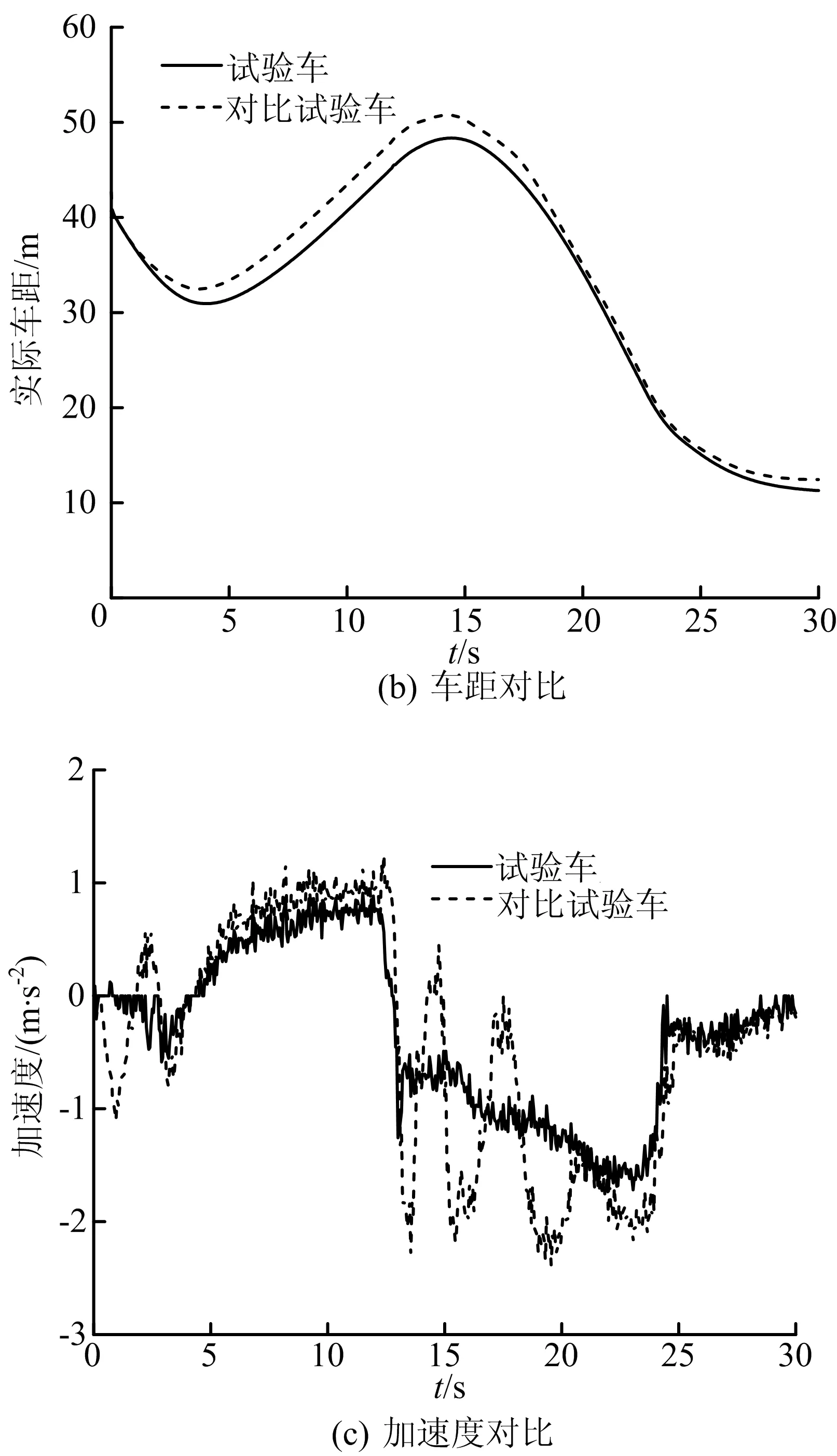
图3 2次试验结果对比

对比试验加速度统计结果见表4所列。

表4 对比试验加速度统计

由试验结果可知,ACC系统启动时ESR毫米波雷达探测到在本车道前方约40 m处存在一辆前车(目标车),此时目标车速度约为32 km/h,试验车速度约为45 km/h。前、后2次试验期望车距策略分别采用TW策略和CW策略,由试验结果的对比可知,2次试验均可实现跟车功能且没有发生碰撞,即实现了跟随性和安全性的目标；但采用TW策略的试验车(第1次试验)在整个跟车阶段(包括加速跟车、减速跟车和静止目标避撞控制阶段)的车速变化频率较低。

从加速度的对比可以看出,在加速跟车阶段采用TW策略的试验车的加速度幅值与对比试验车的加速度幅值均在1 m/s2(绝对值)左右,但采用TW策略的试验车加速度变化较为稳定,且加速度幅值略低，在减速跟车和避撞控制阶段采用TW策略的试验车加速度则表现出较大的优越性(变化频率低且幅值小)。

因此,时变权重策略对于整车经济性和舒适性有较大的改善。

4 结 论

本文首先根据相对车速信息和驾驶员风格设计了VTH策略，并利用路面识别算法进行了修正;然后设计了自适应权重和时变预测模型的自适应MPC控制器,并利用松弛因子和控制增量进行改进;最后通过对比仿真和试验结果得出，时变权重的自适应MPC相比于固定权重的MPC控制策略对复杂的路况适应性更好,能迅速地调整控制器权重,提升系统的乘坐舒适性和鲁棒性。