基于逆子结构法的方向盘怠速振动问题研究

王 维, 陈 剑, 戎芳明, 陶善勇, 庄学凯

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 噪声振动工程研究所,安徽 合肥 230009)

0 引 言

轻卡在市区行驶怠速工况较多,方向盘振动会增加驾驶员的疲劳感,因此方向盘的怠速振动特性会直接影响驾驶员对汽车品牌的评价[1]。

方向盘怠速振动是由发动机振动激励通过不同的传递路径传递到方向盘,当激励频率与转向系统固有频率耦合时,方向盘会产生较大振动。因此可以从传递路径和模态分析的角度着手分析方向盘怠速振动问题[2]。

传统的传递路径分析方法为了获取非耦合传递函数需要将间接激励源拆除,解耦工作量较大。因此,文献[3]提出了基于系统传递函数求解子结构传递函数的逆子结构方法;文献[4]将逆子结构方法用于汽车NVH研究;文献[5]提出了逆子结构传递路径分析方法。逆子结构传递路径分析方法可以利用耦合状态下的系统传递函数,求解子结构非耦合传递函数和悬置动刚度,与传统传递路径方法相比,该方法节省了大量的解耦工作。

本文讨论的某型轻卡在进行NVH性能对标实验时发现,其在怠速定置工况下方向盘振动过大。针对此问题,本文通过模态分析方法和逆子结构传递路径分析方法查找故障原因和关键传递路径,据此提出了优化措施,优化后样车方向盘振动达到了设计要求。

1 逆子结构传递路径分析原理

1.1 传递路径分析基本原理

传递路径分析理论将系统分为激励源、传递路径及响应3个部分。振动传递路径分析方法将目标点响应定义为所有路径贡献量之和[6],即

(1)

其中,y(w)为目标点的响应;Hi(w)为第i条结构路径的非耦合传递函数;Fi(w)为第i条结构路径载荷。

1.2 逆子结构分析模型及原理

根据逆子结构原理,子结构非耦合传递函数和连接刚度可以由耦合状态下的系统传递函数解耦得到,本文将逆子结构分析方法引入方向盘传递路径分析,用于求解子结构非耦合传递函数和动力总成悬置动刚度。

将动力总成至方向盘振动响应的传递路径划分为A、B 2个子结构,子结构通过弹簧耦合连接,如图1所示,动力总成视为子结构B,动力总成悬置被动端到方向盘响应点视为子结构A,耦合自由度为动力总成悬置。

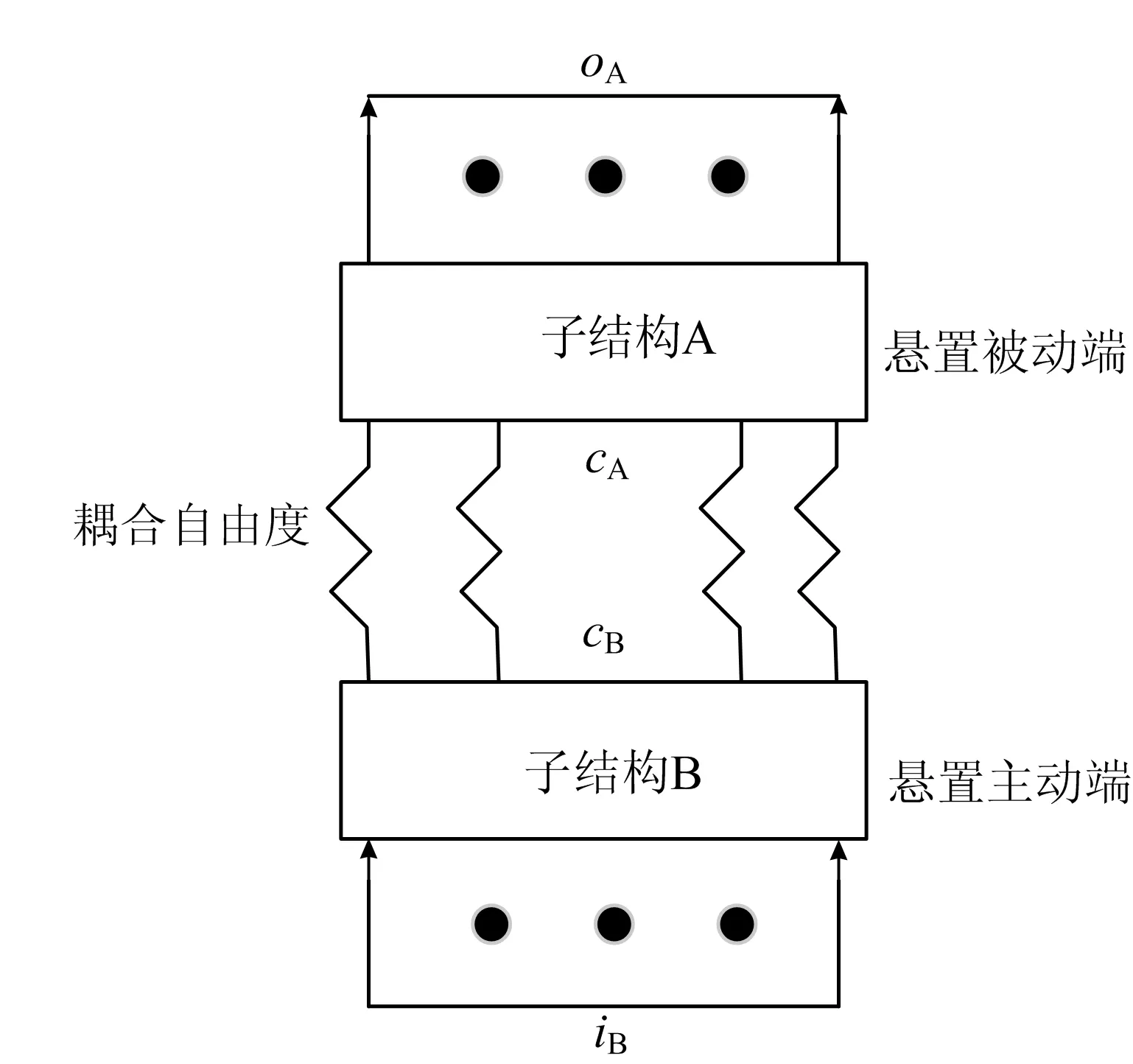
图1 方向盘振动子结构模型

iB为作用于子结构B的激励,即动力总成激励;oA为子结构A的响应,即方向盘振动加速度测点的加速度响应;cA、cB分别为子结构A和子结构B的耦合自由度,即动力总成悬置的耦合自由度[7]。

系统传递函数、子结构传递函数、动刚度K的关系[8]可以表示为:

(2)

(3)

(4)

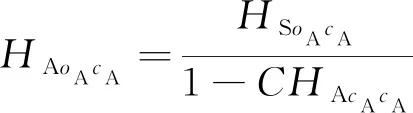
(5)

(6)

其中,HS为系统耦合层面的传递函数;HA、HB分别为子结构A、子结构B的非耦合传递函数;C为动柔度。由此可以从系统耦合传递函数求解得到子结构非耦合传递函数HAoAcA和子结构连接动刚度K,因此称为逆子结构法,该方法避免了传统传递路径分析过程中繁琐的解耦过程,应用前景广阔。

2 方向盘振动测试与模态分析

2.1 方向盘振动测试

本文所研究的卡车在发动机怠速关空调工况下,转速标定在750 r/min,发动机四缸四冲程,二阶发火频率大约为25 Hz。针对主观评价反映的方向盘怠速振动过大的问题,利用振动测试系统进行方向盘振动测试。振动坐标系采用汽车坐标系相同的方向,坐标原点O取方向盘中心点,测点取方向盘6点钟方向,测试采集3个方向的振动加速度。

测试车辆怠速定置时有开空调和关空调2个工况,分别在2个工况下采集方向盘的振动加速度,结果见表1所列,其中g=9.8 m/s2,下文同。

表1 方向盘怠速振动加速度

由表1可知,开空调和关空调工况下都是Z方向的振动加速度最大,X方向次之,Y方向最小;并且开空调时发动机转速上升,振动加速度反而降低。

怠速关空调工况下振动加速度频谱如图2所示。由图2可知,方向盘3个方向在26 Hz附近振动加速度最大,与发动机二阶激励频率25 Hz非常靠近,由此考虑发动机怠速关空调工况下二阶激励频率与转向系统模态频率耦合,下文将对转向系统进行模态测试验证。

图2 方向盘怠速关空调工况下振动频谱

2.2 转向系统约束模态分析

对方向盘和转向柱单独进行自由模态分析时需要将方向盘和转向柱从车上拆卸,花费时间较长,因此将方向盘和转向柱看成转向系统进行约束模态测试,约束模态能够更好地显示转向系统的真实工作特性[9]。使用锤击法对转向系统进行约束模态测试,模态测试振动传感器测点如图3所示。

图3 模态测试振动传感器测点

模态参数识别可得转向系统一阶X向弯曲模态频率和二阶Y向弯曲模态频率为 25.90、31.54 Hz,一阶X向弯曲模态振型如图4所示。

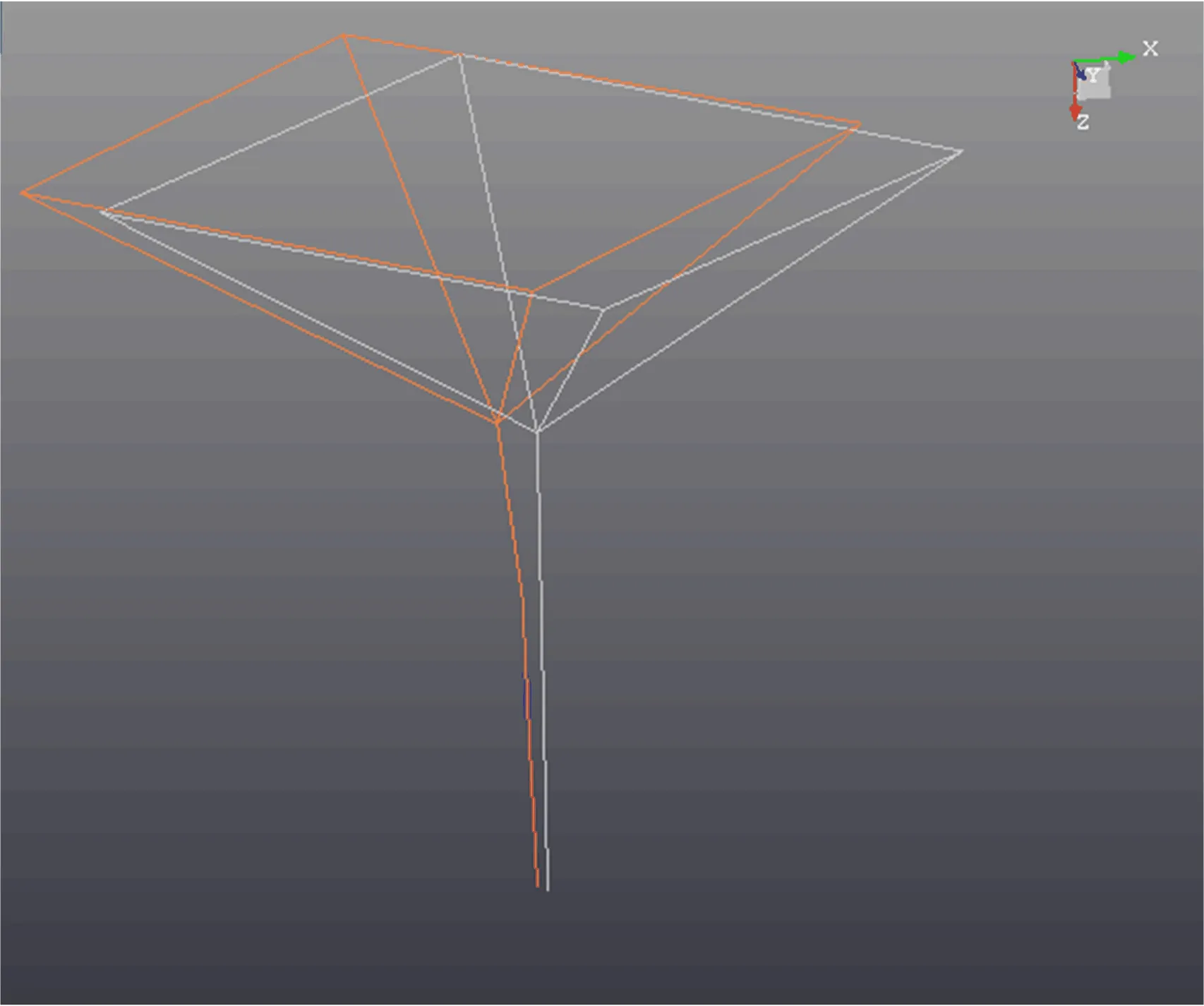
图4 一阶X向弯曲模态振型

由图4可知,一阶X向弯曲模态频率与方向盘怠速关空调工况下振动加速度最大的频率26 Hz基本相同,与发动机怠速关空调二阶激励频率相差1 Hz。

由此可知,怠速关空调工况下振动加速度过大的主要原因之一是怠速关空调工况下发动机二阶激励频率与转向系统一阶X向约束模态频率耦合。因为降低转向系统的一阶弯曲模态频率可能导致开空调工况下,发动机二阶激励频率与转向系统其他阶固有频率耦合,所以采用提高转向系统的一阶弯曲模态频率的措施来降低方向盘振动,一阶弯曲模态频率应高于开空调工况下发动机二阶激励频率。

3 逆子结构传递路径分析

3.1 数据采集与路径解耦

方向盘振动的传递路径较多,全部分析比较复杂,并且本文只分析怠速工况方向盘振动,此时路面激励不需要考虑,因此本文只分析动力总成悬置对方向盘的传递路径[10]。每个悬置考虑X、Y、Z3个方向自由度,由方向盘振动测试结果可知,X方向和Z方向的振动加速度比Y方向振动加速度要大得多,因此只考虑方向盘X方向、Z方向的振动响应,共计4×3×2=24条传递路径,响应点取与方向盘振动水平测试相同的点。逆子结构传递路径实验分析流程如下,其中最核心的工作是利用逆子结构法进行解耦。

(1) 怠速工况数据采集。采集方向盘振动响应信号、动力总成主被动端信号。

(2) 测试系统耦合频响函数。在耦合状态下测试系统层面频响函数。

(3) 逆子结构法获取子结构非耦合频响函数和动刚度。获得动力总成悬置动刚度及子结构非耦合频响函数。

(4) 载荷识别。采用悬置动刚度法识别载荷。

(5) 路径贡献量计算与分析。根据载荷与频响函数计算分析每条路径的贡献量。

采集系统耦合频响函数时需要采集HScAcA、HScBcB、HScAcB、HScBcA、HSoAcA共5个12×2规模的频响函数[11],直接测量工作量大,因此采用间接法测量,其原理为:

Hoi(f)=Hoe(f)[Hee(f)]-1Hie(f)

(7)

其中,e为替代激励点,取车架靠近动力总成悬置处。采用间接法测量,只需测量HScAe、HScBe、HSoAe和一次原点频响函数HSee,大大减少了测量工作量,其中替代激励点原点响应如图5所示。间接法求得系统耦合频响函数,其中左前悬置被动端X向至方向盘X向耦合频响函数如图6所示。

图5 替代激励点原点响应

将测量、计算得到的系统耦合频响函数代入(2)～(6)式,计算得到子结构非耦合频响函数HAoAcA和动刚度K。

HAoAcA为动力总成悬置被动端至方向盘振动响应点的非耦合频响函数,共12×2个频响函数,其中右后悬置至方向盘Z向的非耦合频响函数如图7所示。K为动力总成悬置的动刚度,共4×3个,其中右后悬置3个方向的动刚度如图8所示。

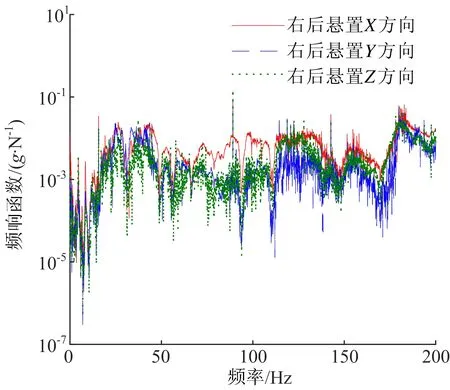
图7 右后悬置被动端至方向盘Z向非耦合频响函数

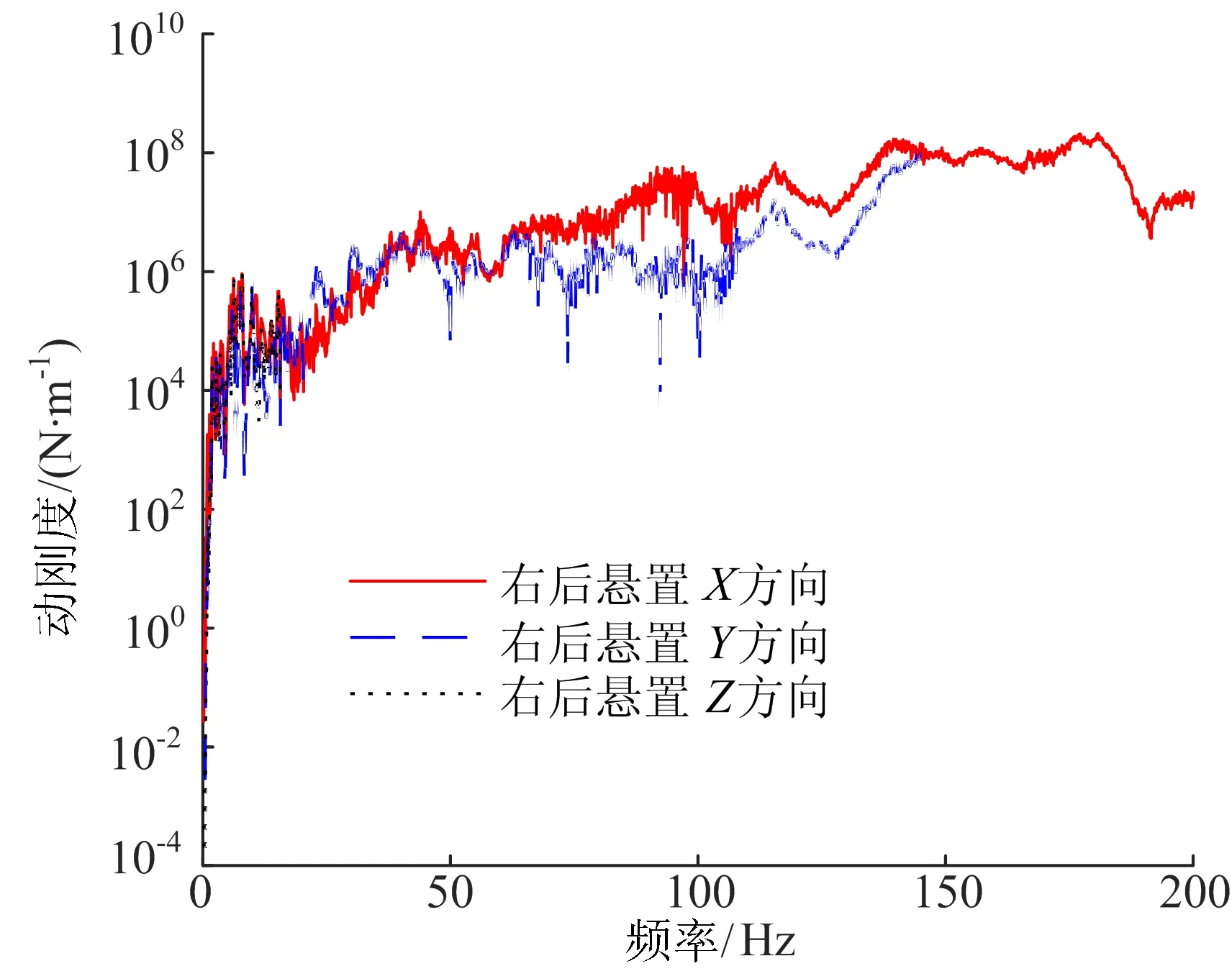
图8 右后悬置动刚度

3.2 怠速工况载荷获取

采用悬置动刚度方法进行载荷识别,其表达式为:

(8)

其中,aai(f)、api(f)分别为第i个路径悬置主动端和被动端振动加速度频谱;Ki为使用逆子结构方法求得的悬置动刚度。求解得到动力总成4个悬置的载荷,其中右后悬置的载荷最大,左后悬置次之。

右后悬置和左后悬置载荷如图9所示。由图9可知,右后悬置和左后悬置载荷在二阶激励频率25 Hz附近都有峰值,这也印证了发动机是主要激励源。

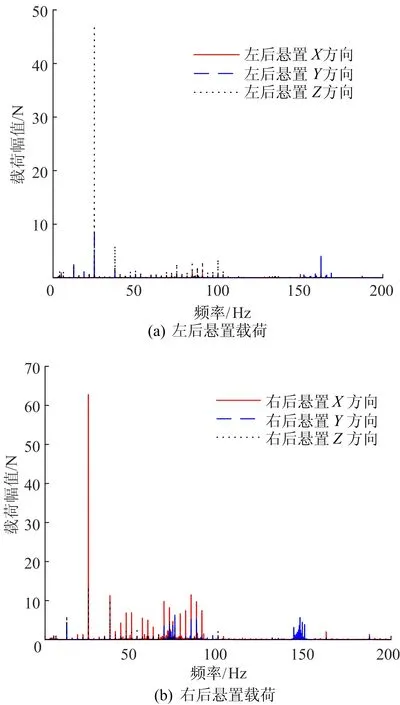
图9 各路径载荷

3.3 各路径振动贡献量分析

将3.1节通过逆子结构法求得的各路径非耦合传递函数与3.2节识别的悬置载荷代入(1)式,计算得到各条传递路径对方向盘怠速工况下X、Z2个方向振动的贡献量。

路径贡献量计算结果如图10所示。其中路径顺序为左前悬置、左后悬置、右前悬置、右后悬置、合成值、测试值。

由图10可以看出,方向盘X向振动贡献量最大的是右后悬置X向、右后悬置Y向；方向盘Z向振动贡献量最大的是右后悬置X向、左后悬置Z向。

由贡献量分析可知,4个悬置中右后悬置贡献量最大,并且右后悬置X向的贡献量最大;合成值和测试值之间的误差很小,验证了逆子结构传递路径分析方法的有效性。综上所述,可以根据贡献量分析结果针对性地对右后悬置动刚度进行优化。

图10 路径贡献量

4 方向盘振动控制

根据以上分析,针对发动机二阶发火频率和转向系统一阶约束模态频率耦合的问题,提出增加转向柱支架厚度和轻量化方向盘的改进措施。优化后的转向系统一阶约束模态频率提高到怠速关空调发动机二阶激励频率5 Hz以上。针对个别路径贡献量过大的问题,提出提高后悬置横梁的刚度和优化悬置橡胶垫刚度的改进措施。

优化前、后关空调怠速工况下,方向盘振动加速度见表2所列。由表2可知,改进后方向盘怠速振动加速度明显下降,效果明显,方向盘振动水平与对标车辆达到同一水平。

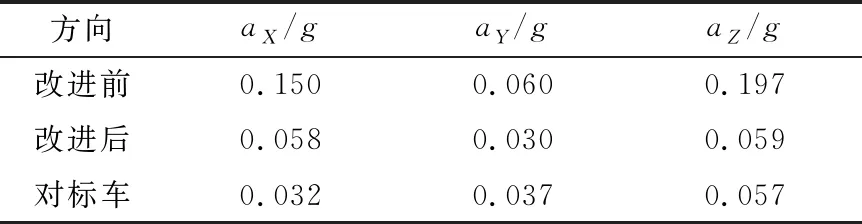
表2 方向盘改进前、后怠速振动加速度

5 结 论

(1) 本文通过方向盘振动测试和约束模态测试,发现发动机二阶激励频率与转向系统一阶弯曲模态频率耦合是该型轻卡方向盘怠速振动过大的主要原因之一。

(2) 将逆子结构法引入传递路径分析,利用逆子结构法获取子结构非耦合传递函数和动力总成悬置动刚度,对方向盘振动进行传递路径贡献量分析,发现右后悬置X向是影响该型轻卡方向盘怠速振动的关键路径。

根据模态分析和逆子结构传递路径分析结果,有针对性地提出了多项改进措施,样车改进后方向盘振动加速度明显降低,达到了设计要求,同时验证了该方法的有效性。