黄麻纤维混凝土的动态压缩力学性能研究

仰 涛, 王宝珍, 罗皓鹏

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

混凝土是一种应用极为广泛的建筑材料,但素混凝土脆性特征明显,抗拉强度低,抵抗裂纹的能力较弱,因此应用时有一定的局限性。通过在素混凝土中加入各类纤维,可以提高混凝土的抗拉性能、韧性及抗裂性能等。不同于钢纤维对混凝土的增强性能,柔性纤维对混凝土的改性主要体现在韧度方面,可以提高混凝土结构在高速冲击时的缓冲吸能性能。柔性的天然植物纤维(如黄麻、剑麻、椰壳及竹纤维等)均可取自于大自然,通过大量种植来获得。相比于人工合成纤维,天然纤维拥有易于获取、价格低廉、可降解及绿色环保等优点。随着全世界对环境问题的日益关注,天然纤维在建筑材料中的合理利用近来引起了研究者的极大兴趣[1-2],不仅如此,对于一些大量种植农作物的发展中国家来说,天然纤维代替合成纤维的使用则有着更为重要的意义。

20世纪90年代中期,埃及的M.Samir对棕榈树叶纤维混凝土进行了研究,从微观角度解释其对混凝土抗拉强度的增强机理。文献[3]在较高的纤维含量下,红麻纤维混凝土抗压强度略低于普通混凝土,但试样的裂缝更均匀,在弯曲破坏时更表现出了延性破坏的特征,可应用于抗冲击构件;文献[4]研究发现黄麻纤维能够抑制裂缝的延伸,减少裂缝尖端的应力集中现象,并能延缓裂缝的扩展速度;文献[5]发现掺入黄麻纤维降低了砂浆的平均相对开裂指数,明显改善了砂浆的抗裂性能。

对植物纤维混凝土动态力学性能的研究要滞后于静态,目前尚处于起步阶段。文献[6]提出与素混凝土相比较,剑麻纤维混凝土的抗冲击性能最高提升近30%;文献[7]中短散黄麻纤维对混凝土抗拉、抗弯性能有较好提升,纤维在承受冲击破坏中存在被拔出和断裂的现象,表现出了对能量的吸收等特性;文献[8]通过落锤试验得出，掺入混杂竹纤维可延缓混凝土的初期开裂,并且提高混凝土的整体变形能力,起到增韧和吸能的作用。以上研究着重讨论植物纤维影响混凝土力学性能的机理,得到了一些有意义的定性结论。但对于植物纤维混凝土的力学性能随应变率和纤维含量变化的定量分析存在不足,不利于工程应用。本文基于分离式霍普金森压杆(split-Hopkinson pressure bar,SHPB)单轴冲击压缩试验,研究黄麻纤维混凝土(jute fiber reinforced concrete,JFRC)的动态力学行为。分析其抗压强度的应变率效应,定义韧度指数来反映纤维混凝土的吸能特性,得到了动态增强因子和韧度指数随应变率、纤维体积分数变化的经验公式。这些研究有利于促进植物纤维混凝土在建筑行业中的应用。

1 试 验

1.1 试样制备

试样混凝土材料配合比见表1所列。

表1 混凝土配合比

其中水泥标号为P·O 32.5R,碎石的最大粒径为10 mm。试样中添加长度约20 mm的黄麻纤维,如图1所示,黄麻纤维的特性参数见表2所列。

图1 试样中的黄麻纤维

表2 黄麻纤维特性参数

本文共制作了5种组别试样,其黄麻纤维体积分数φJ分别为0%(素混凝土)、0.5%、1.0%、1.5%、2.0%,采用湿法混合[9],有利于纤维和骨料充分拌和。将搅拌好的混凝土拌合物装入刷好脱模剂的模具中,分层捣实、抹平放到振动台上振动,待表面浮现水泥浆时停止振动,最后抹平收浆。将成型的试样水平放置24 h后拆模,编号后标准养护28 d。试样包括用于动态的直径70 mm、厚度35 mm的圆盘试样和用于静态实验的直径70 mm、高度150 mm的圆柱试样,动态试验试样如图2所示。为保证试验结果准确性,对标准养护后的试样端面进行磨削加工,控制其表面不平整度在0.05 mm以内。

图2 试验试样

1.2 试验方法

静态试验和动态压缩试验分别采用电子万能试验机和直径74 mm直锥变截面SHPB完成。电子万能试验机如图3所示,采用恒速率加载至试件破坏,记录破坏荷载,对不同纤维体积分数的试样进行3次重复试验,取平均值。SHPB实验装置简图如图4所示。

图3 静态压缩试验装置

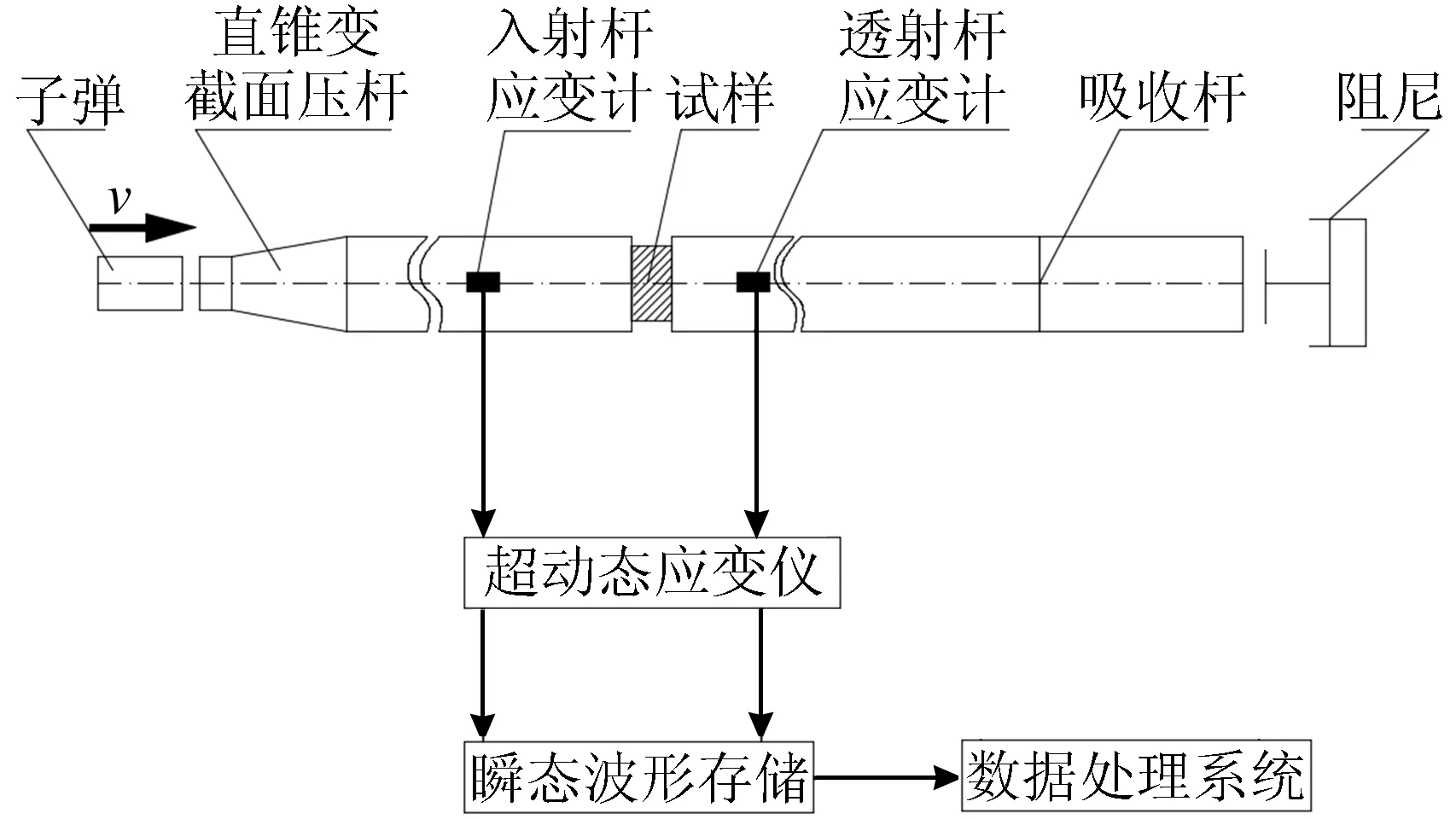
图4 动态压缩试验装置简图

根据压杆上电阻应变计测量得到入射波εi(t)、反射波εr(t)和透射波εt(t),采用经典两波法得到试样的应力-应变曲线和应变率时程曲线,即

(1)

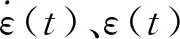
图5 不同应变率下JFRC的应力-应变曲线

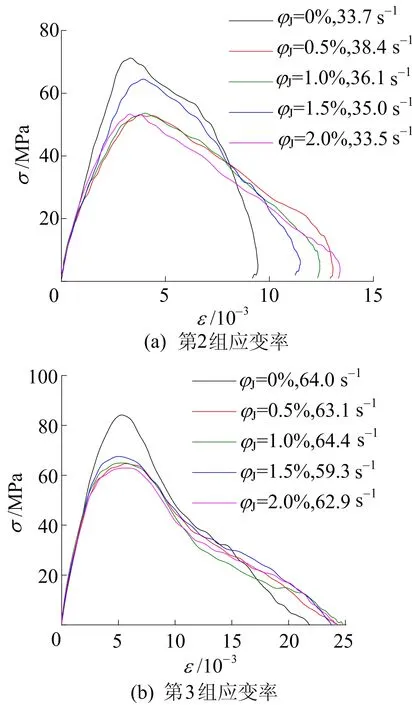
图6 不同体积分数JFRC的应力-应变曲线

2 试验结果及分析

2.1 动态应力-应变曲线及破坏形态分析

从图5可以看出,不同应变率下,黄麻纤维混凝土的应力-应变曲线具有显著的应变率效应,其抗压强度随应变率的增加而增加,增加的幅度同时又与纤维的体积分数有关;抗压强度对应的破坏应变也随着应变率的增加而增加。

从图6可以看出,在相近应变率下,所有类别混凝土应力-应变曲线的初始阶段基本呈线性且重合,与素混凝土相比,黄麻纤维混凝土虽然抗压强度有所降低,但破坏应变有所提高,其线性段之后的应力-应变曲线呈现曲率更小的圆弧,卸载段更平缓。

从图7可以看出,相近应变率下,素混凝土试验后呈散块状碎裂破坏,随着纤维体积分数的增加,试验后试样的完整性越来越好,纤维体积分数1.5%时试样形态最完整,体积分数增加至2.0%时,试样形态虽然基本完整,但裂缝显著增多。

结合黄麻纤维混凝土的微观结构对上述试验现象进行分析可知，在受力变形过程中,首先混凝土基体起主要承载作用,此时微裂纹缓慢扩展,纤维的作用不显著,应力-应变曲线表现为相同的近似线弹性阶段。而进入裂纹快速扩展阶段后,纤维对于混凝土基体具有如下2种作用：① 增加了原始缺陷；② 细化裂纹并对裂纹扩展有桥联阻裂作用。其中原始缺陷的增加导致混凝土承载能力降低,裂纹的细化及纤维阻裂则反映在应力-应变曲线上升段及卸载段更平缓、抗压强度对应的应变更大及破坏后试样的完整性更好,即试样的韧性随纤维的加入而改善。

2.2 黄麻纤维混凝土抗压强度

2.2.1 准静态抗压强度与纤维体积分数的关系

文献[10]指出,虽然许多因素都影响着应变率对混凝土抗压强度的增强效应,但混凝土的静态强度始终具有至关重要的影响。试验得到的混凝土静态抗压强度随纤维体积分数的变化关系如图8所示,其值在基体强度20%范围内波动。黄麻纤维掺入混凝土将产生2种效应:一方面增加了混凝土内部缺陷,原生裂纹数量更多;另一方面黄麻纤维在裂纹扩展中具有桥联阻裂作用。混凝土静态强度的波动正体现了这2种效应的耦合关系:① 掺入纤维后纤维产生缺陷的影响总体大于其阻裂效应,但纤维掺量的不同,使2种效应造成的影响也不同;② 当掺入纤维体积分数较低时,纤维产生缺陷的影响较大,混凝土强度下降较大;③ 继续增加纤维掺量,其阻裂效应增强,混凝土强度回升;④ 若纤维掺入超过一定比例,则混凝土强度将再次下降。因此,从维持混凝土静态抗压强度方面,黄麻纤维的掺量有一个最佳比例,本文得到的为1.5%,此时纤维混凝土强度比基体强度仅下降约5%。

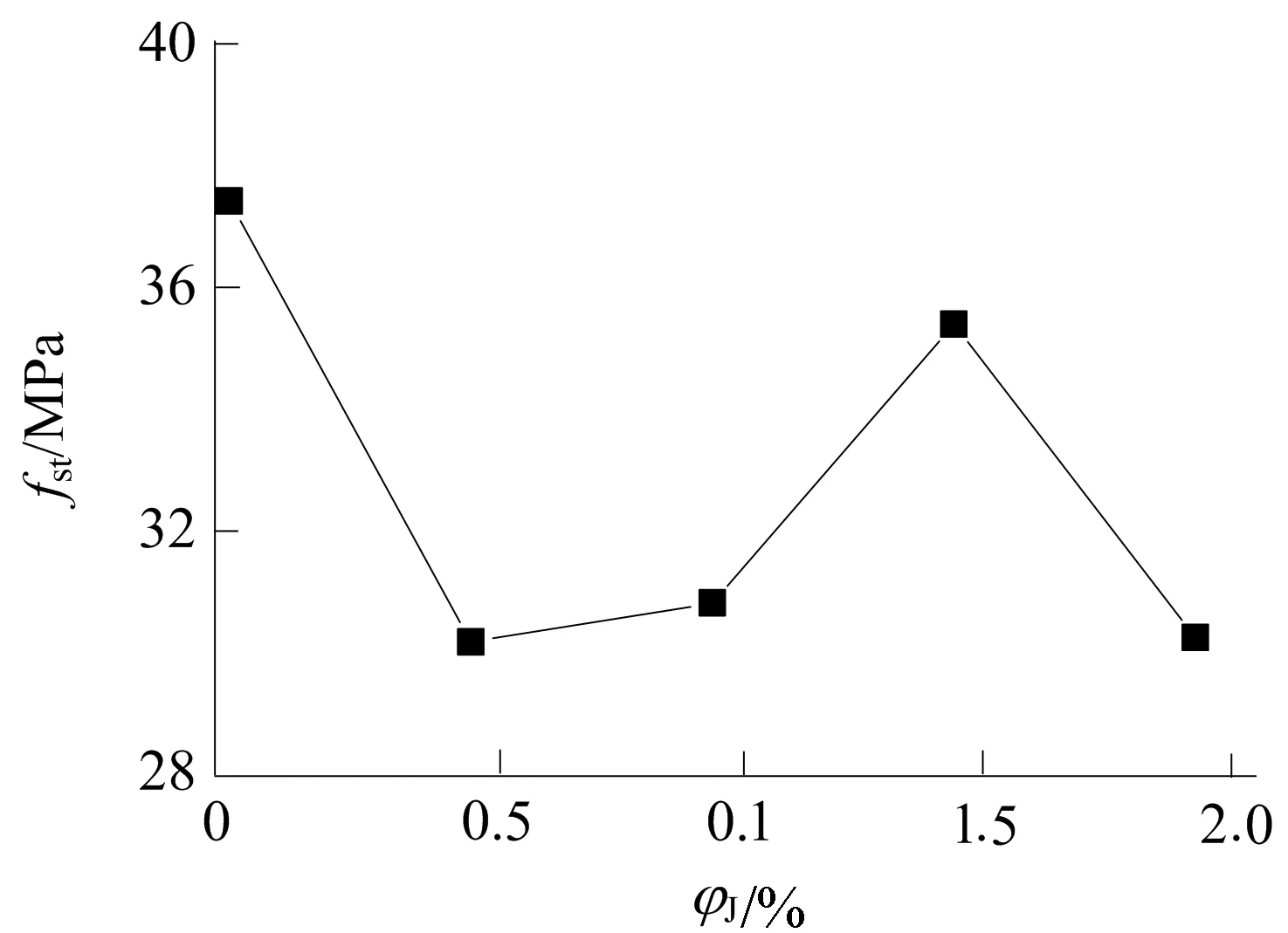
图8 准静态下不同体积分数JFRC的抗压强度

2.2.2 动态抗压强度与应变率的关系

动态抗压强度是衡量材料在动荷载作用下的强度规律的重要力学性能指标。为了更明确反映强度的应变率效应,本文采用黄麻纤维混凝土的动态与静态抗压强度的比值-动态增强因子[11](dynamic increase factor,DIF)进行研究。采用下列函数来描述:

(2)

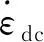
(3)

其中:φJ为黄麻纤维的体积分数,拟合结果如图9所示,其中JFRC的5条拟合曲线的相关系数R2范围为0.95～0.98。

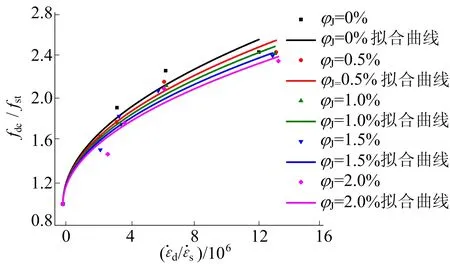
图9 JFRC的动态强度增强因子-应变率曲线

根据图9和(2)式、(3)式可知:① 黄麻纤维混凝土抗压强度的动态增强因子随应变率的增加显著增加,但相近应变率下基本都小于素混凝土;② 在相近应变率下,随着纤维体积分数的增加,动态增强因子降低;③ 随纤维体积分数增加,动态增强因子随应变率增加的趋势更平缓。因此,黄麻纤维混凝土抗压强度的动态增强因子对应变率的敏感性要低于素混凝土,并且纤维体积分数越高这种敏感性就越低。

2.3 黄麻纤维混凝土吸能特性分析

根据上述分析,黄麻纤维对混凝土性能的提高主要表现在增韧方面。在动态下既能有效改善混凝土脆性破坏特点,又提高其破坏阶段的缓冲吸能能力。材料的总吸能特性可以通过总应变能密度反映,但它是强度和延性的综合体现,不足以反映纤维在混凝土破坏阶段的作用。借鉴钢纤维混凝土韧度指数[12]的定义,采用韧度指数η来反映加入黄麻纤维后混凝土吸能性能,即

(4)

其中,Wmax为总的应变能密度;W0.85fdc为应力值达到抗压强度85%时对应的应变能密度,主要反映基体弹性变形吸收能量。这样定义的η消除了材料强度对吸能性能的影响,η越大则黄麻纤维混凝土卸载段吸收的能量越多。韧度指数η随应变率的变化关系如图10所示。

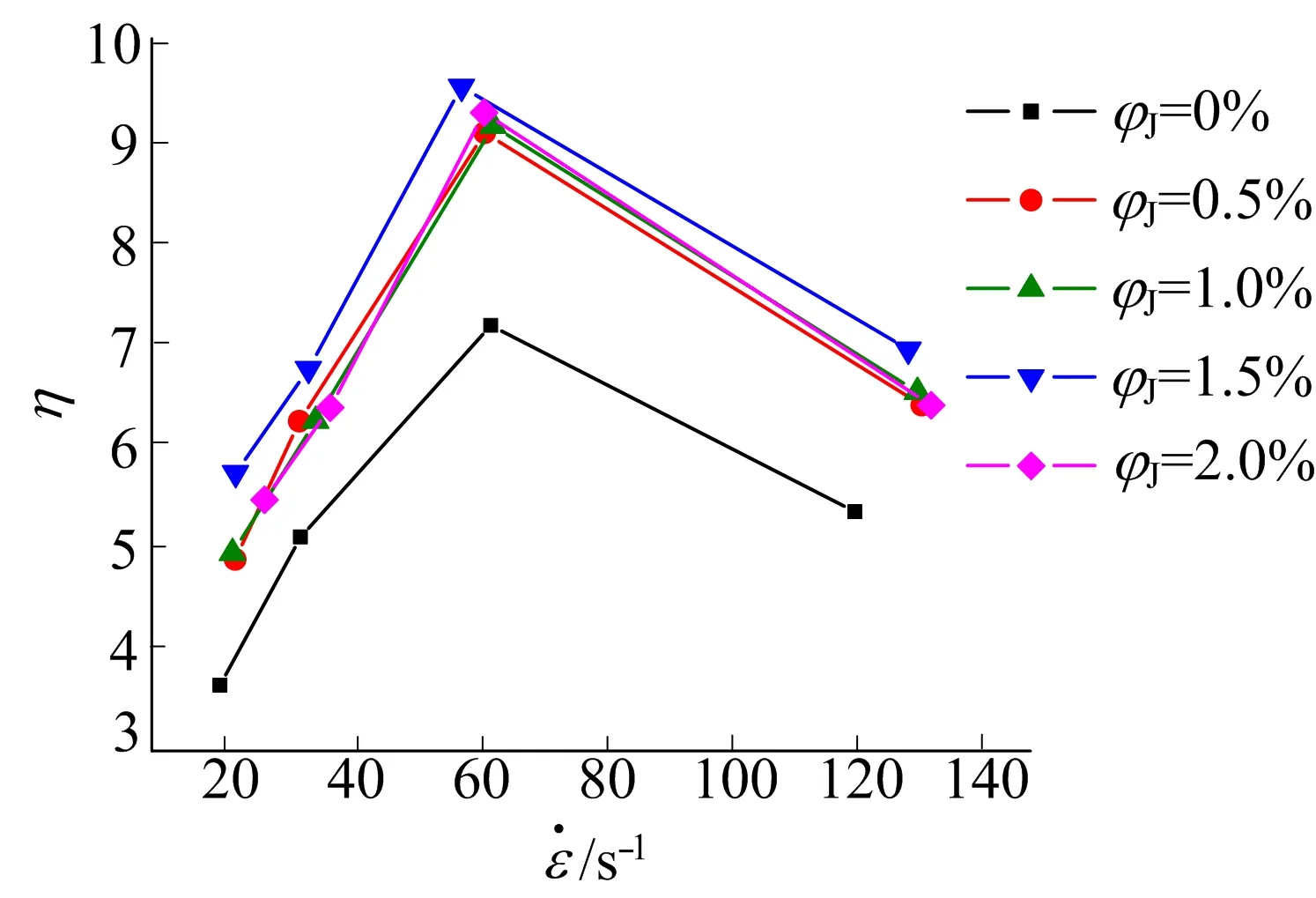
图10 JFRC韧度指数-应变率曲线

不同应变率下韧度指数η随纤维体积分数的变化关系如图11所示,根据其形态,选择二次函数进行拟合，即

(5)

其中,A为某一组应变率下素混凝土的韧度指数η;B、C为拟合参数。B、C由试验数据拟合为:

(6)

图11的4条拟合曲线相关系数R2的范围为0.95～0.97。

从图10、图11可以看出,黄麻纤维混凝土韧度指数η均大于素混凝土,黄麻纤维的掺入改善了混凝土的韧度,提升了吸能能力。随着应变率增加韧度指数先增加后降低。这是由于在高应变率下,混凝土由韧转脆的机制使得试样的韧性降低。对称轴为韧度指数η达到最大时对应的φJ值,即某一应变率下吸能最优的纤维体积分数见表3所列,表3中数据均在1.5%左右。结合抗压强度与体积分数之间的关系可知，在体积分数为1.5%时,黄麻纤维混凝土拥有最佳的吸能性能,同时也具有掺入纤维后的最高抗压强度。

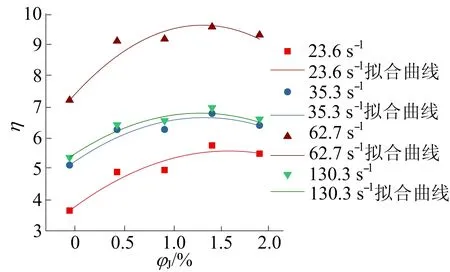
图11 JFRC韧度指数-体积分数曲线

表3 η-φJ拟合曲线的系数

3 结 论

本文利用SHPB实验装置,对黄麻纤维混凝土的动态压缩力学性能进行了研究,主要结论如下:

(1) 黄麻纤维的加入有效提高了混凝土的韧性。破坏应变的变化规律、应力-应变曲线更为平缓的卸载段以及试样破坏形态完整性的改善均验证了这点。

(2) 黄麻纤维混凝土抗压强度的动态增强因子随着应变率增加而增加,在相近应变率下,黄麻纤维混凝土抗压强度动态增强因子小于素混凝土,并且纤维体积分数越高,其值越小。在试验数据的基础上提出了经验公式。据此公式可知,随着应变率增加,黄麻纤维混凝土的动态抗压强度增加。同时,动态抗压强度可以看作是静态抗压强度、应变率效应以及纤维体积分数三者耦合的结果。

(3) 为了量化纤维的吸能作用,提出了韧度指数的经验公式。黄麻纤维混凝土的韧度指数均大于素混凝土,黄麻纤维的体积分数在1.5%左右时韧度指数最大,吸能效果最明显。