THE EFFECT OF REFUGE AND PROPORTIONAL HARVESTING FOR A PREDATOR-PREY SYSTEM WITH REACTION-DIFFUSION∗†

Xueru Lin

(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,Fujian,PR China)

Abstract

Keywords reaction-diffusion system;iteration method;global asymptotical stability;prey refuge;proportional harvesting

1 Introduction

To accurately describe the real ecological interactions between some species such as lynx and hare,mite and spider mite,sparrow and sparrow hawk,etc.described by Wollkind et al.[1]and Tanner[2],Robert May proposed a Holling-Tanner predatorprey model[3],in which the author incorporated Holling’s rate[4,5].In[6],Hsu and Huang studied the following predator-prey system

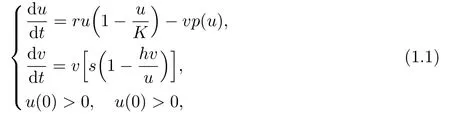
whereuandvare the populations of the prey and the predator respectively.Kis the carrying capacity of the prey andris the intrinsic growth rate in the absence of predation.sis the intrinsic growth rate of the predator andp(u)is the functional response.The carrying capacity of the predator is proportional to the population size of the prey.By using Dulacs criterion and constructing Liapunov functions,they established the global stability of the positive locally asymptotically stable equilibrium of system(1.1).For more biological background of system(1.1),one could refer to[6-8]and the references cited therein.

Taking into account the distribution of the prey and predators in spatial location within a fixed bounded domain Ω⊂RN(N≤3),Wonlyul Ko and Kimun Ryu[9]considered a Holling-Tanner predator-prey system with reaction-diffusion.In[10],Peng and Wang studied the following system

whereu(x,t)andv(x,t)are the species densities of the prey and predator respectively.The constantsdi(i=1,2)are the diffusion coefficients of prey and predator respectively.n is the outward unit normal vector on the smooth boundary∂Ω.The initial datasu0(x)andv0(x)are continuous functions on,the homogeneous Neumann boundary condition means that the system is self-contained and has no population flux across the boundary∂Ω.Obviously,as mentioned in[10],the above system has a unique coexisting positive equilibrium,where

They studied the stability of the positive constant solution of system(1.2)and obtained sufficient conditions for the global stability of the positive equilibrium by constructing a suitable Lyapunov function.For the ecological sense of system(1.2)we can refer to[10]and the references cited therein.

Recently,Chen and Shi[11]reconsidered the above system(1.2),and proved that if

holds,then the unique constant equilibrium of system(1.2)is globally asymptotically stable,which shows that condition(1.4)is simpler and weaker than the condition obtained in[10].

As is well known,the existence of refuge has important effects on the coexistence of prey and predators,and research on the dynamic behaviors of predator-prey model with prey refuges has become a popular topic during the last decade[12-21].If we extend model(1.2)by incorporating a refuge protectingsuof the prey,wheres∈[0,1)is a constant,(1−s)uof the prey is available to the predator.Modifying model(1.2)accordingly becomes the following model:

Clearly,biological resources in the predator-prey model are most likely to be harvested and sold with the purpose of achieving the economic interest which motivates the introduction of harvesting in the predator-prey model.If we subject each population to a proportional harvesting effort specific to the population,the equations of model(1.2)become the following model

where constantsei(i=1,2)are harvesting efforts on respective populations.

To the best of the author’s knowledge,seldom did scholars consider effect of the refuge and the proportional harvesting.Specially,to this day,still no scholars investigate whether the refuge and the proportional harvesting can influence the global stability of the positive equilibrium of system(1.2)or not.

Motivated by the above question,the main concern of this paper is to study the effect of the refuge and the proportional harvesting.More concretely,in the following section we will investigate that the unique interior equilibrium of system(1.5)is globally asymptotically stable under some simple conditions by using upper and lower solutions method,and we will also discuss the influence of the prey refuge.Secondly,we will discuss the influence of the proportional harvesting in Section 3.Finally,we end this paper with a brief conclusion in Section 4.

2 The influence of Prey Refuge

It is easy to verify that system(1.5)has a unique positive equilibrium(u∗,v∗),where

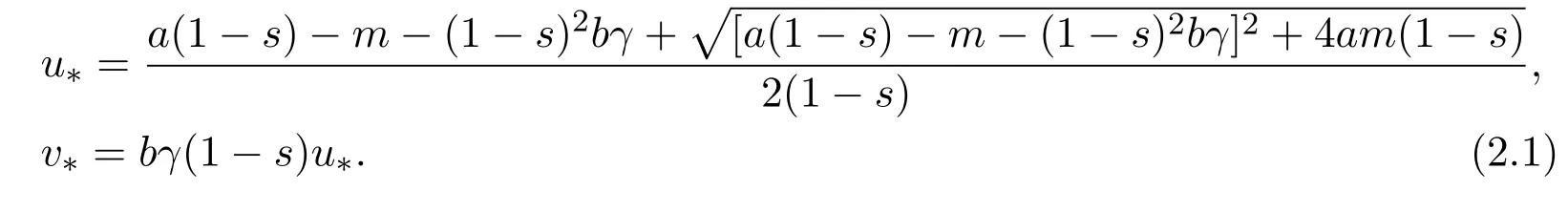
Now,we give the result of the global stability of(u∗,v∗)for system(1.5),which implies the prey and predators are spatially homogeneously distributed as the time converges to infinity.

Theorem 2.1Assume that

then the positive equilibrium(u∗,v∗)is globally attractive for system(1.5),that is,for any initial values u0(x)>0,v0(x)>0,

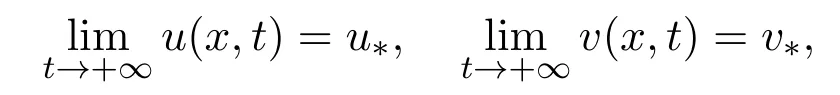
uniformly for x∈.

ProofIt is well known that ifc>0 andω(x,t)satisfies the equation

thenω(t,x)→cuniformly forx∈Ω ast→+∞(see[9]).

Since(2.2)holds,we can choose anε0satisfying

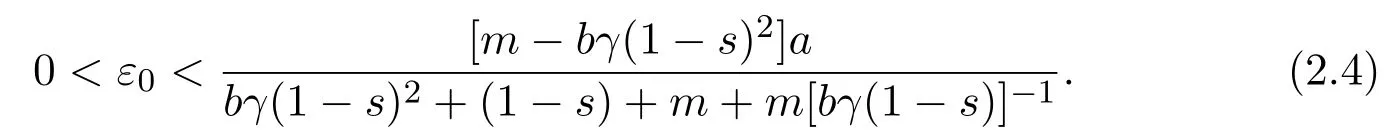
From the first equation of system(1.5),we can easily obtain that

then from comparison principle of parabolic equations,there exists at1>0 such that for anyt>t1,,where.

Therefore,from the second equation of system(1.5),we have

fort>t1.Hence there exists at2>t1such that for anyt>t2,,where.Again this implies

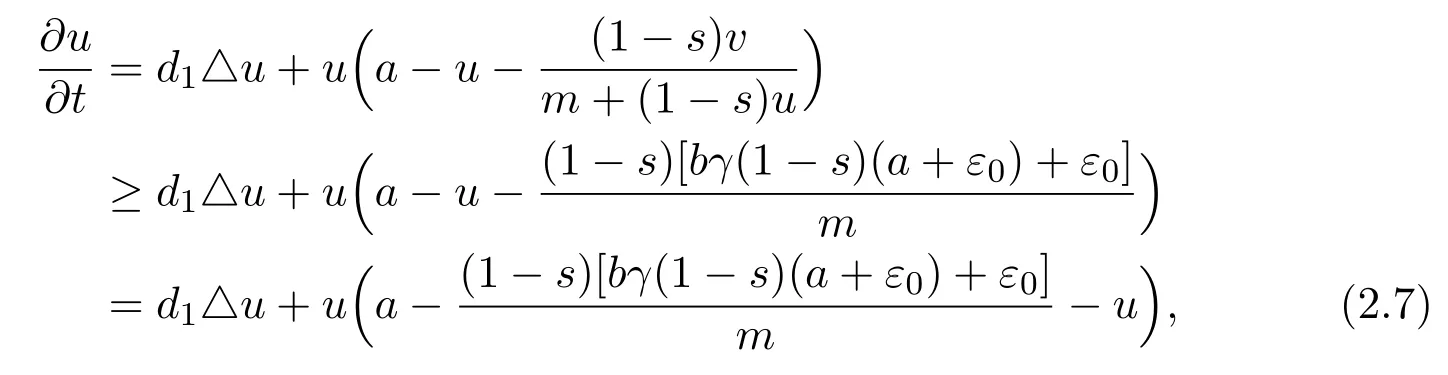
fort>t2.Since(2.2)holds,forε0chosen as in(2.4),there are

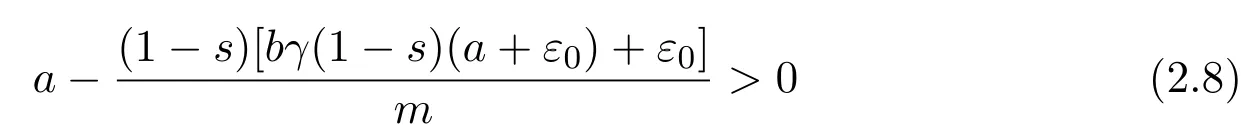
and

Hence there exists at3>t2such that for anyt>t3,,where

Finally we apply the lower bound ofuto the second equation of system(1.5),and have

(2)无涂层的原始石墨片在在1500 ℃空气中焙烧2.5 h后就完全被烧掉．1号～6号试样在1500 ℃空气中焙烧16 h后失重率W分别为69.45%，1.97%，-0.60%，46.06%，58.91% 和 0.58%．重新制备3号样，试样在1500 ℃空气中焙烧86 h后失重率W为-5.26%，这进一步证明了3号试样经历长时间高温氧化不仅没有氧化失重，反而增重了．这说明，3号试样图涂层抗高温氧化效果最好．

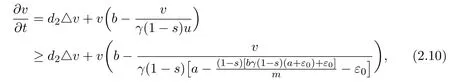
fort>t3.Since forε0chosen as in(2.4),

Then there exists at4>t3such that for anyt>t4,,where

Therefore,fort>t4we obtain that

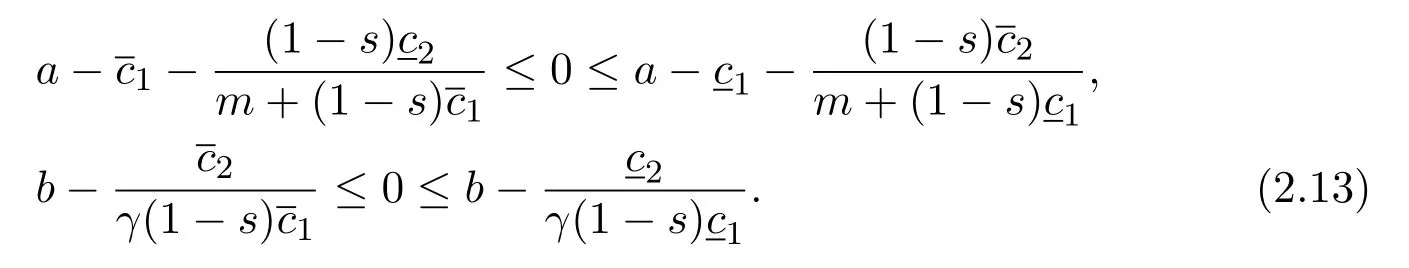
The inequalities(2.13)show thatandare a pair of coupled upper and lower solutions of system(1.5)as in the definition in[22,23],as the nonlinearities in(1.5)are mixed quasimonotone.It is clear that there exists aK>0 such that for any

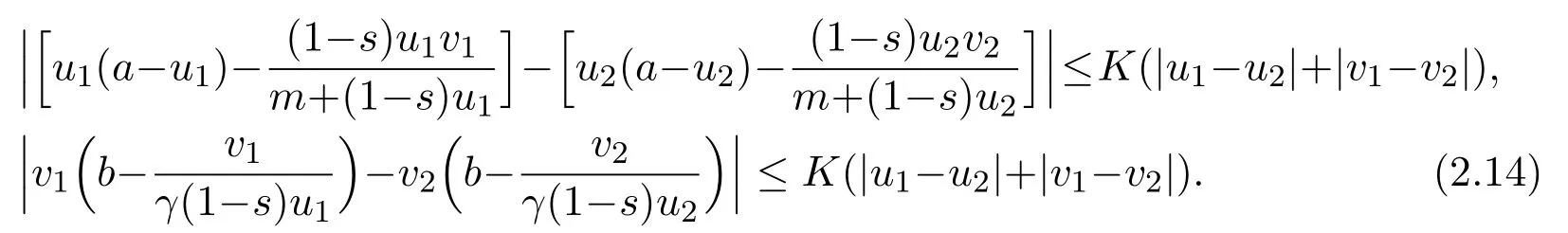
We define two iteration sequencesas follows:Forn≥1,

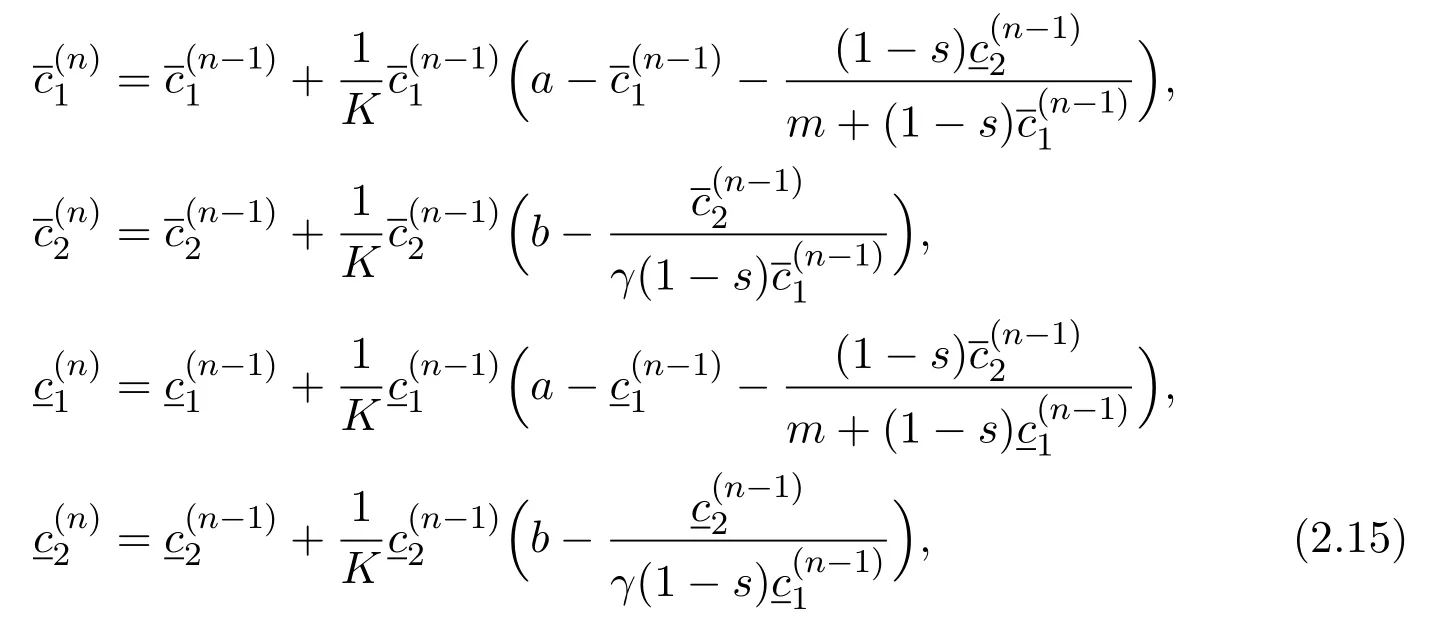
So

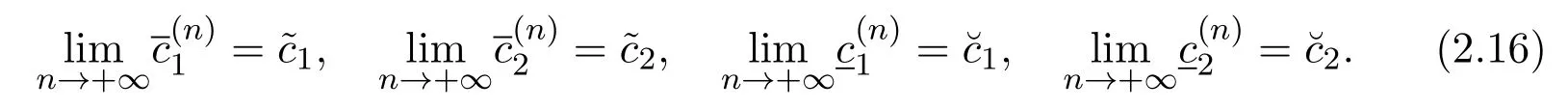
Hence,from(2.15)and(2.16)we have

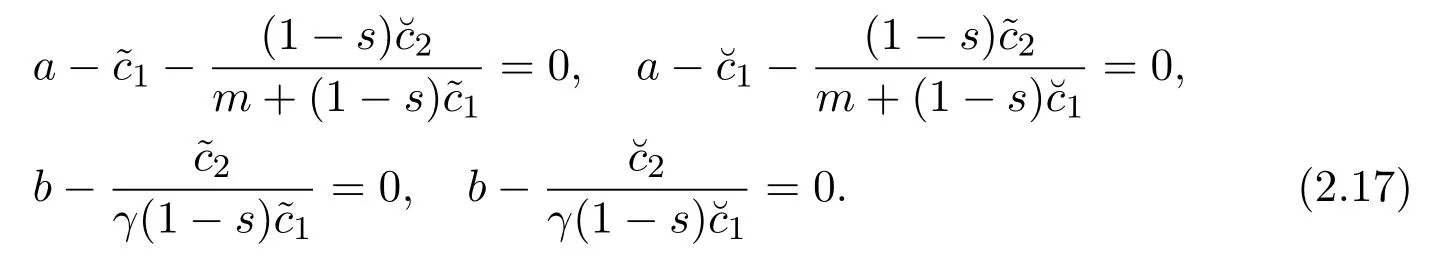
Simplifying(2.17)we obtain

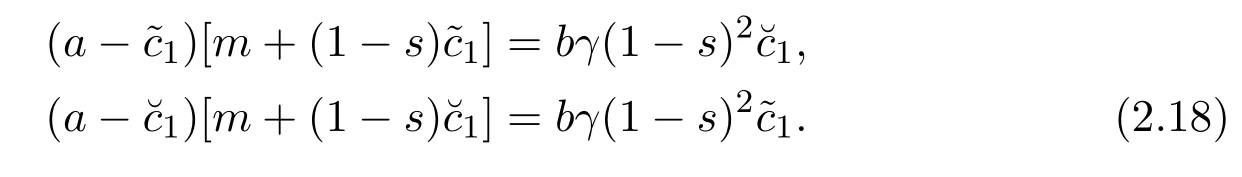
Subtracting the first equation of(2.18)from the second equation of(2.18),we can obtain that

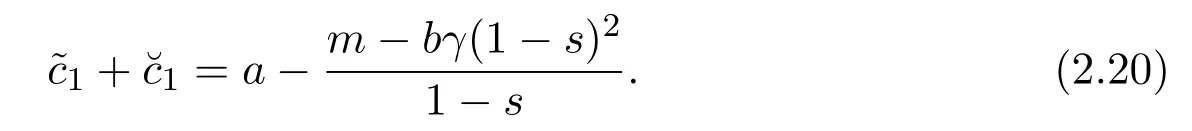
Substituting equation(2.20)into(2.18),we have

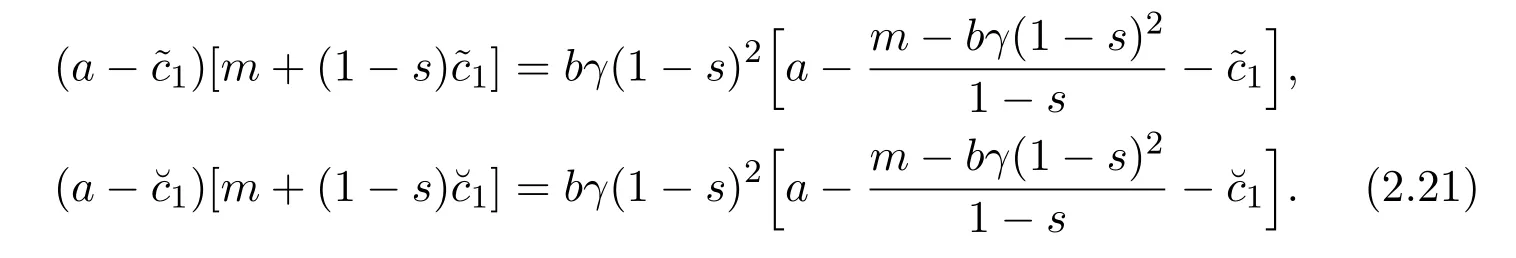
Hence the following equation

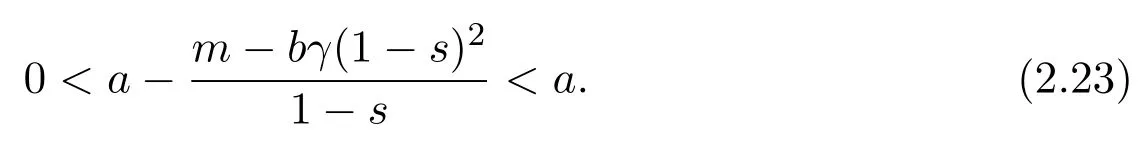
(2.22)can be written as follows

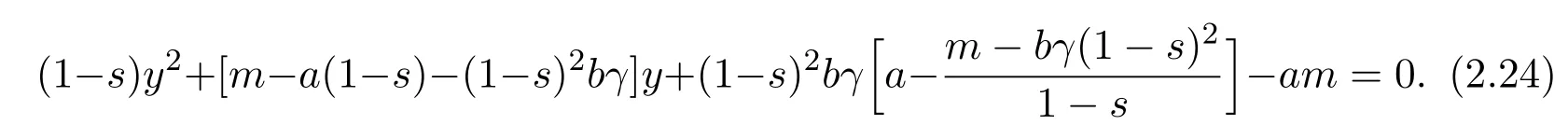
From(2.2)and(2.23),it follows that

From(2.25),we can easily obtain that(2.22)do not exist two positive roots.Hence,and consequently,Then from the results in[17,18],the solution(u(x,t),v(x,t))of system(1.5)satisfies

uniformly forx∈.So the constant equilibrium(u∗,v∗)is globally asymptotically stable for system(1.5).

This completes the proof of Theorem 2.1.

Remark 2.1If we consider system(1.5)withs=0,Theorem 2.1 is reduced to the main results of Chen and Shi[11],so our results generalize the main results in[11].

Remark 2.2In[11],Chen and Shi considered system(1.2).Under the assumptionm>bγ,the unique positive equilibrium of system(1.2)is globally asymptotically stable.In Theorem 2.1,we obtain that ifm>bγ(1−s)2holds,then the unique positive equilibrium of system(1.5)is globally asymptotically stable.One can show that the parameter region given bym>bγ(1−s)2is contained in the set given bym>bγ.That is,ifm>bγholds,thenm>bγ(1−s)2also holds.It is shown that the prey refuge has influence on the global asymptotical stability of unique positive equilibrium of system(1.5),furthermore,they can change the position of the unique interior equilibrium and make species coexist more easily.

Remark 2.3From condition(2.2)of Theorem 2.1,we can easily obtain that if the suturation constant and refuge constant of prey are large enough,the intrinsic growth rate of predator and the conversion factor of prey into predator are relatively small,then the positive equilibrium(u∗,v∗)is globally attractive for system(1.5).From the viewpoint of biology,this implies that the prey and predator will be spatially homogeneously distributed as the time converges to infinity,no matter what their diffusion coefficients are.

Remark 2.4We will give numerical simulation to show the feasibility of our results.In system(1.5),seta=1;m=2;b=1;γ=1;s=0.5.By computation,one has

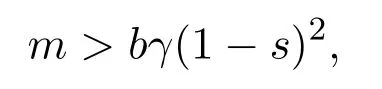
then condition(2.2)of Theorem 2.1 holds.Figure 1 shows the dynamics behavior of system(1.5).

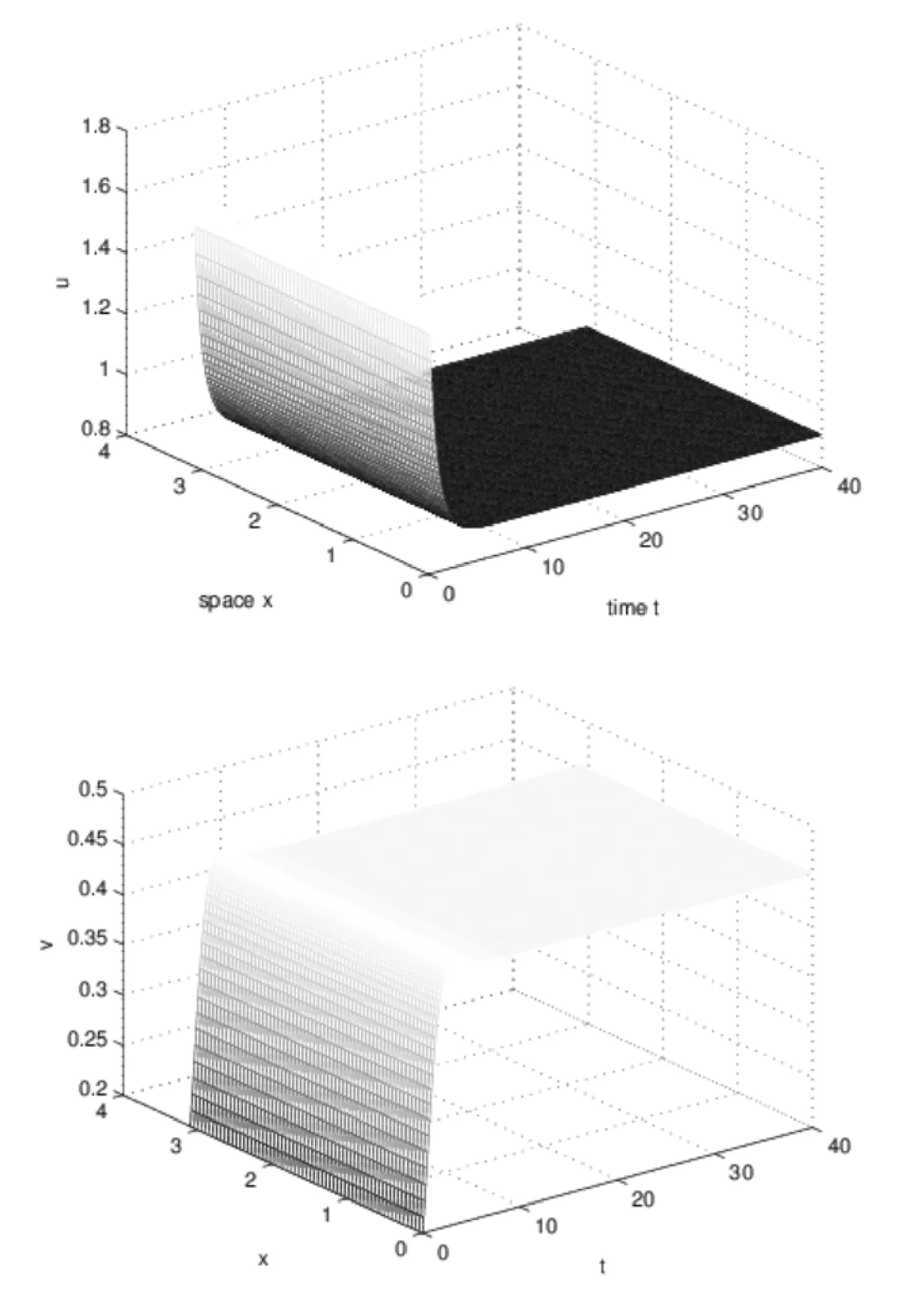
Figure 1:Dynamics behavior of system(1.5)with a=1;m=2;b=1;γ=1;s=0.5.

3 The influence of Proportional Harvesting

By simple computation,system(1.6)admits a unique positive equilibrium(u,v)=(u∗,v∗),if

holds,where

Similar to the proofs of Theorem 2.1 in Section 2,by using upper and lower solutions method,we can easily obtain the following theorem.

Theorem 3.1If(3.1)and the following inequality

holds,then the unique positive equilibrium of system(1.6)is globally asymptotically stable.

Remark 3.1From Theorem 3.1,we obtain that under assumption(3.1),ifm>(b−e2)γholds,then the unique positive equilibrium of system(1.6)is globally asymptotically stable.One can also show that the parameter region given bym>(b−e2)γis contained in the set given bym>bγ.It is also shown that under some assumption,the proportional harvesting has influence on the global asymptotical stability of unique positive equilibrium of system(1.6),furthermore,they can change the position of the unique interior equilibrium and make species coexist more easily.As we know,biological resources in the prey-predator system are most likely to be harvested and sold with the purpose of achieving the economic interest.From Theorem 3.1,if we choose and control the harvesting effortsei,i=1,2,appropriately,we can not only harvest the biological resources and achieve the economic interest,but also protect the biological resources.

Remark 3.2We will give numerical simulation to show the feasibility of our results.In system(1.6),seta=1;m=2;b=1;γ=1;e1=0.5;e2=0.5.By computation,one can easily obtain that conditions(3.1)and(3.3)of Theorem 3.1 hold.Figure 2 shows the dynamics behavior of system(1.6).

4 Conclusion and Discussion

In this paper,by using upper and lower solutions combined with the iteration method,we obtain the global asymptotical stability of systems(1.5)and(1.6).It is shown that the prey refuge and the proportional harvesting have influence on the global asymptotical stability of unique positive equilibrium of system(1.2),furthermore,they can change the position of the unique interior equilibrium and make species coexist more easily.Indeed,similar to proofs of Theorem 2.1 in Section 2,we can easily obtain that the unique positive equilibrium of the following diffusive predator-prey system with prey refuge and proportional harvesting

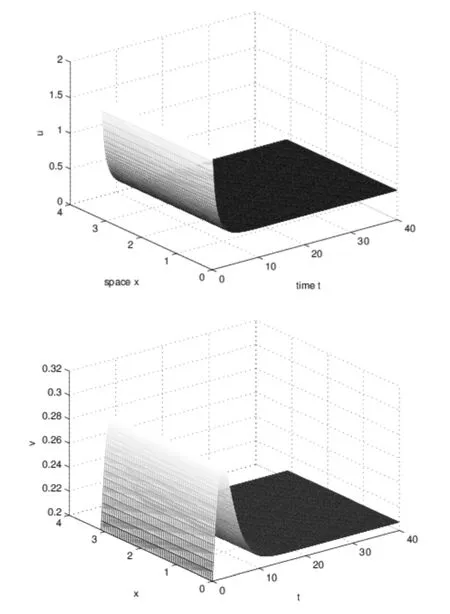
Figure 2:Dynamics behavior of system(1.6)with a=1;m=2;b=1;γ=1;e1=0.5;e2=0.5.

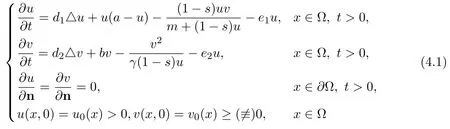
is also globally asymptotically stable,if

and

hold.Therefore,if we choose and control the prey refuge parameter and the harvesting efforts appropriately,we can not only harvest the biological resources and achieve the economic interest,but also protect the biological resources.